Two balls AandB are thrown with speeds uandu/2, respectively. Both the balls cover the same horizontal distance before returning to the plane of projection. If the angle of projection of ball Bis15∘ with the horizontal, then the angle of projection of A is.
sin−1(18)
12sin−1(18)
13sin−1(18)
14sin−1(18)
The correct Answer is:B
To solve the problem, we need to find the angle of projection of ball A, given that both balls A and B cover the same horizontal distance before returning to the plane of projection.
1. Identify the Given Information:
- Speed of ball A = u
- Speed of ball B = u2
- Angle of projection of ball B = 15∘
2. Use the Range Formula:
The horizontal range R of a projectile is given by the formula:
R=u2sin2θg
where u is the initial speed, θ is the angle of projection, and g is the acceleration due to gravity.
3. Write the Range for Both Balls:
- For ball A (angle of projection = θ):
RA=u2sin2θg
- For ball B (angle of projection = 15∘):
RB=(u2)2sin30∘g=u24⋅12g=u28g
4. Set the Ranges Equal:
Since both balls cover the same horizontal distance:
RA=RB
Therefore:
u2sin2θg=u28g
5. Cancel Common Terms:
We can cancel u2g from both sides (assuming u≠0):
sin2θ=18
6. Find the Angle θ:
To find θ, we take the inverse sine:
2θ=sin−1(18)
Therefore:
θ=12sin−1(18)
Final Answer:
The angle of projection of ball A is:
θ=12sin−1(18)
- Speed of ball A = u
- Speed of ball B = u2
- Angle of projection of ball B = 15∘
The horizontal range R of a projectile is given by the formula:
R=u2sin2θg
where u is the initial speed, θ is the angle of projection, and g is the acceleration due to gravity.
- For ball A (angle of projection = θ):
RA=u2sin2θg
- For ball B (angle of projection = 15∘):
RB=(u2)2sin30∘g=u24⋅12g=u28g
Since both balls cover the same horizontal distance:
RA=RB
Therefore:
u2sin2θg=u28g
We can cancel u2g from both sides (assuming u≠0):
sin2θ=18
To find θ, we take the inverse sine:
2θ=sin−1(18)
Therefore:
θ=12sin−1(18)
The angle of projection of ball A is:
θ=12sin−1(18)
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Multiple Correct11videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Assertion - Reasoning5videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Subjective40videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Integer9videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression2videos
KINETIC THEORY OF GASES
Similar Questions
Two bodies P and Q are projected with velocites √2 u and u respectively. They cover the same horizontal distance. If body P is projected at 15∘ will the horizontal, then calcu late the angle of projection of body Q.
View SolutionTwo balls are projected from the same point with such a speed that both reach the same point on ground at a distance of 19.6√3m from the point of projection. If one of the particles is projected at an angle of 30∘ with the ground, then calculate the time of flight of the second ball.
View Solution
Knowledge Check
- Question 1 - Select One
Two projectiles A and B thrown with speeds in the ratio 1 : √2 acquired the same heights. If A is thrown at an angle of 45∘ with the horizontal, the angle of projection of B will be
A0∘B60∘C30∘D45∘ - Question 2 - Select One
A ball is projected horizontally with a speed v from the top of the plane inclined at an angle 45∘ with the horizontal. How far from the point of projection will the ball strikes the plane?
A2v2gB√2[2v2g]Cv2gD√2v2g - Question 3 - Select One
Two balls are thrown with the same speed from a point O at the same time so that their horizontal ranges are same. If the difference of the maximum height attained by them is equal to half of the sum of the maximum heights, then the angles of projection for the balls are
A15∘,75∘B30∘,60∘C0∘,90∘D37∘,53∘
A ball projected with a velocity of 28 m/sec has a horizontal range 40 m. Find the two angles of projection.
View SolutionTwo projectiles A and B thrown with speeds in the ratio 1 : √2 acquired the same heights. If A is thrown at an angle of 45∘ with the horizontal, the angle of projection of B will be
View SolutionA ball is projected from ground with a speed 70m/s at an angle 45∘ with the vertical so that it strikes a vertical wall at horizontal distance 4903m from the point of projection. If the ball returns back to the poin tof projection without any collision with ground then find the coefficient of restitution between the ball and wall.
View SolutionA ball thrown down the incline strikes at a point on the incline 25m below the horizontal as shown in the figure. If the ball rises to a maximum height of 20m above the point of projection, the angle of projection α (with horizontal x axis) is
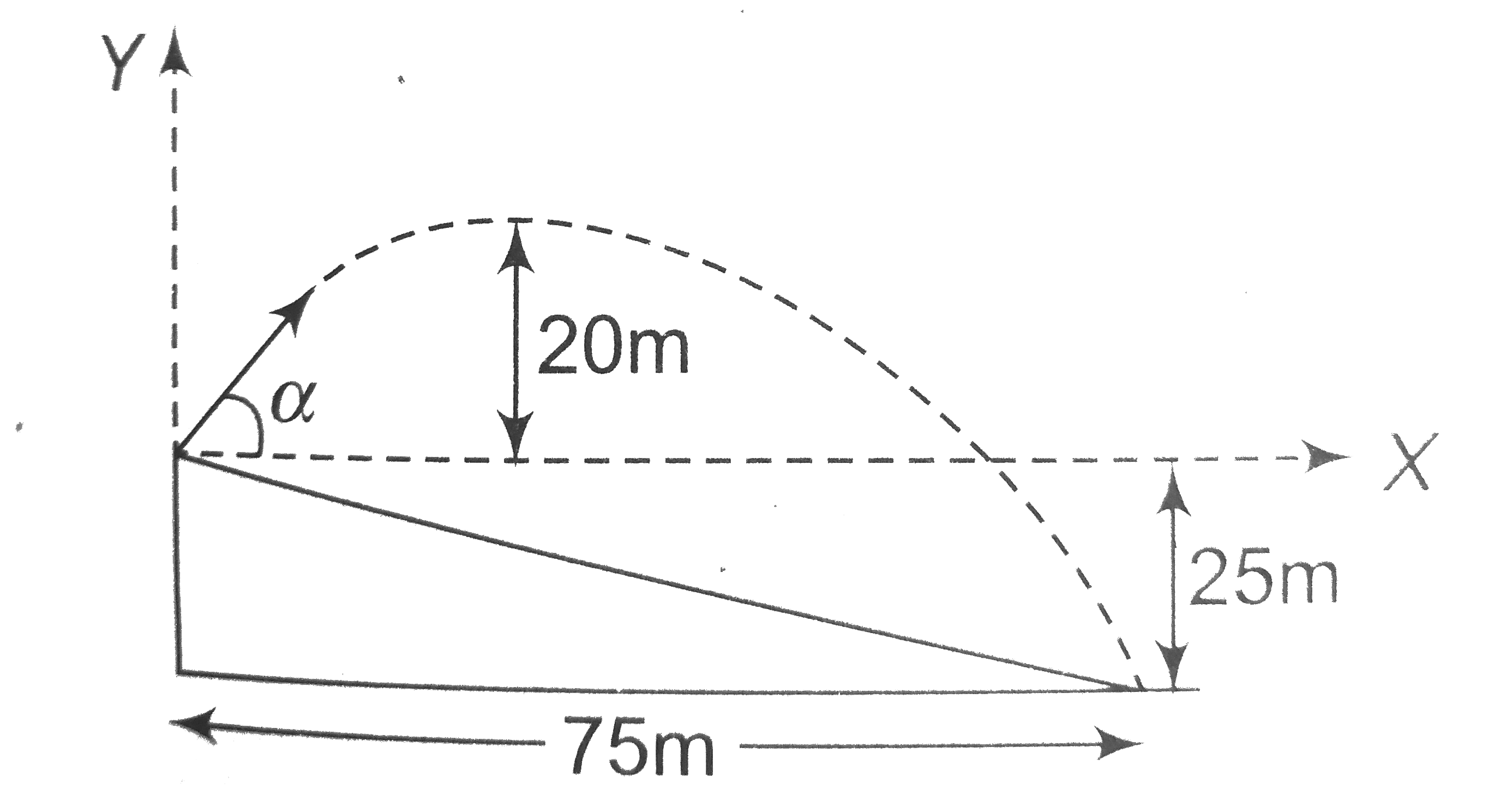 View Solution
View SolutionA ball thrown by a boy is caught by another after 2 sec . some distance away in the same level. If the angle of projection is 30∘, the velocity of projection is
View Solution

