Two balls A and B of masses m and 2 m are in motion with velocities 2v and v, respectively. Compare: Their inertia.
To compare the inertia of two balls A and B with masses m and 2m, and velocities 2v and v respectively, we can follow these steps:
1. Identify the Masses of the Balls:
- Let the mass of ball A be m.
- Let the mass of ball B be 2m.
2. Understand the Concept of Inertia:
- Inertia is the property of a body to resist changes in its state of motion. It is directly proportional to the mass of the body. Therefore, the greater the mass, the greater the inertia.
3. Set Up the Inertia Comparison:
- The inertia of ball A can be represented as IA and the inertia of ball B as IB.
- Since inertia is proportional to mass, we can express this as:
IA∝mandIB∝2m
4. Formulate the Ratio of Inertia:
- Now, we can compare the inertia of both balls:
IAIB=m2m
5. Simplify the Ratio:
- Simplifying the ratio gives:
IAIB=12
6. Conclusion:
- Therefore, the ratio of the inertia of ball A to the inertia of ball B is:
IA:IB=1:2
Final Answer:
The inertia of ball A is to the inertia of ball B as 1:2.
- Let the mass of ball A be m.
- Let the mass of ball B be 2m.
- Inertia is the property of a body to resist changes in its state of motion. It is directly proportional to the mass of the body. Therefore, the greater the mass, the greater the inertia.
- The inertia of ball A can be represented as IA and the inertia of ball B as IB.
- Since inertia is proportional to mass, we can express this as:
IA∝mandIB∝2m
- Now, we can compare the inertia of both balls:
IAIB=m2m
- Simplifying the ratio gives:
IAIB=12
- Therefore, the ratio of the inertia of ball A to the inertia of ball B is:
IA:IB=1:2
The inertia of ball A is to the inertia of ball B as 1:2.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - ICSECHAPTER - LAWS OF MOTIONEXERCISE - TOPIC 3 (2 Marks Questions )
9 Videos
- LAWS OF MOTIONBOOK - ICSECHAPTER - LAWS OF MOTIONEXERCISE - TOPIC 3 (3 Marks Questions )
7 Videos
- LAWS OF MOTIONBOOK - ICSECHAPTER - LAWS OF MOTIONEXERCISE - TOPIC 2 (3 Marks Questions )
11 Videos
- ICSE ANNUAL EXAMINATION -2020BOOK - ICSECHAPTER - ICSE ANNUAL EXAMINATION -2020EXERCISE - SECTION-II
45 Videos
- LIGHTBOOK - ICSECHAPTER - LIGHTEXERCISE - TOPIC 2 Spherical Mirrors (4 Marks Questions )
9 Videos
Similar Questions
Two balls A and B of masses m and 2 m are in motion with velocities 2v and v, respectively. Compare: Their momentum.
View SolutionTwo balls A and B of masses m and 2 m are in motion with velocities 2v and v, respectively. Compare: The force needed to stop them in the same
View SolutionTwo bodies A and B of same mass are moving with velocities v and 2v, respectively. Compare their inertia
View SolutionTwo bodies A and B of same mass are moving with velocities v and 2v, respectively. Compare their momentum.
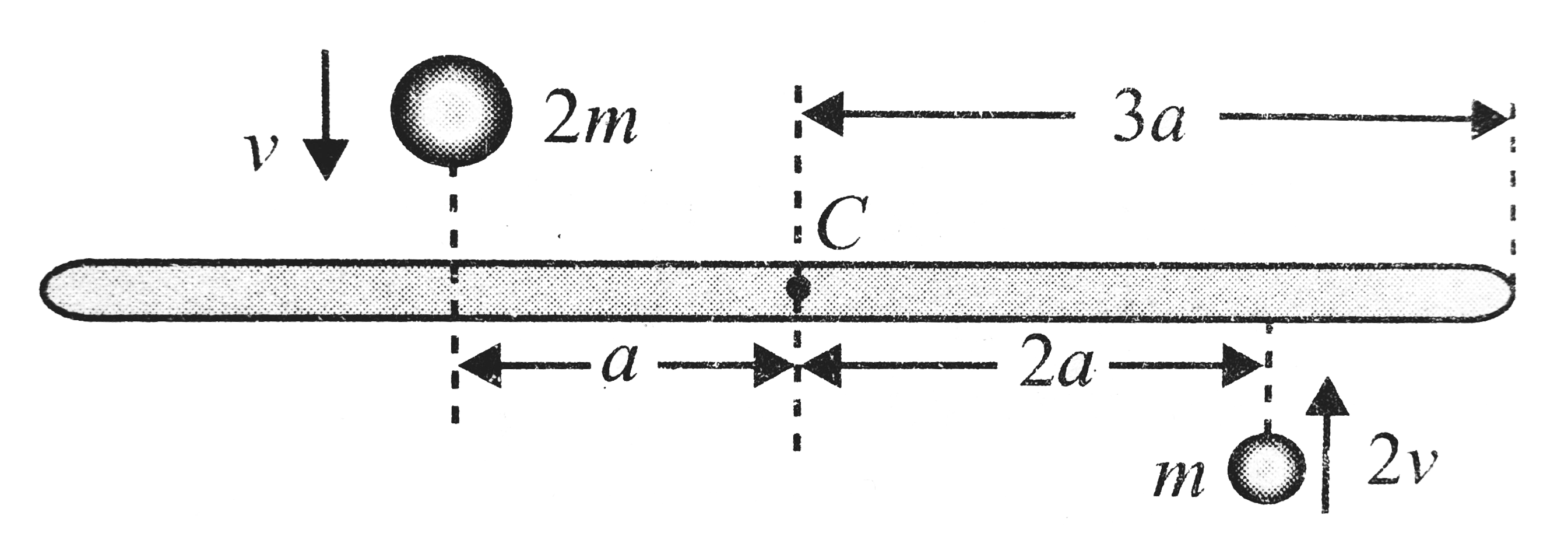
View SolutionA uniform bar of length 6a and mass 8m lies on a smooth horizontal table. Two point masses m and 2m moving in the same horizontal plane with speeds 2v and v, respectively, strike the bar (as shown in the figure) and stick to the bar after collision. Denoting angular velocity (about the centre of mass), total energy and centre of mass velocity by ω, E and VC, respectively, we have after collision
View SolutionTwo particles, A and B of masses m and 3m, are moving along X and Y axes respectively, with the same speed v. They collide at the origin, and coalesce into one body, after the c ollision. What is the velocity of this coalesced mass ?
View SolutionTwo particles of equal mass m are moving with velocities vˆi and v(ˆi+ˆj2) respectively. If the particles collide completely inelastically, then the energy lost in the process is
View SolutionTwo cars of same mass are moving with velocities v1andv2 respectively. If they are stopped by supplying same breaking power in time t1andt2 respectively then v1v2 is
View SolutionTwo particles of masses m1 and m2 in projectile motion have velocities →v1 and →v2 , respectively , at time t=0. They collide at time t0. Their velocities become →v'1 and →v'2 at time 2t0 while still moving in air. The value of ∣∣∣(m1→v'1+m2→v'2)−(m1→v1+m2→v2)∣∣∣
View SolutionTwo particles of mass 2m and m moving with speed v and 2v respectively pependicular to each other collides perfectly inelastically, then

Speed of the particles after collision
View Solution
