Two balls A and B of masses m and 2 m are in motion with velocities 2v and v, respectively. Compare: Their momentum.
To compare the momentum of two balls A and B with given masses and velocities, we can follow these steps:
1. Identify the Masses and Velocities:
- Mass of ball A, mA=m
- Mass of ball B, mB=2m
- Velocity of ball A, vA=2v
- Velocity of ball B, vB=v
2. Write the Formula for Momentum:
- The formula for momentum p is given by:
p=m×v
- Here, p is the momentum, m is the mass, and v is the velocity.
3. Calculate the Momentum of Ball A:
- Using the formula for momentum:
pA=mA×vA=m×(2v)=2mv
4. Calculate the Momentum of Ball B:
- Similarly, for ball B:
pB=mB×vB=(2m)×v=2mv
5. Compare the Momentums:
- Now we can compare the momentum of ball A and ball B:
pA:pB=2mv:2mv
- This simplifies to:
pA:pB=1:1
Conclusion:
The momentum of ball A is equal to the momentum of ball B. Therefore, the ratio of their momenta is 1:1.
---
- Mass of ball A, mA=m
- Mass of ball B, mB=2m
- Velocity of ball A, vA=2v
- Velocity of ball B, vB=v
- The formula for momentum p is given by:
p=m×v
- Here, p is the momentum, m is the mass, and v is the velocity.
- Using the formula for momentum:
pA=mA×vA=m×(2v)=2mv
- Similarly, for ball B:
pB=mB×vB=(2m)×v=2mv
- Now we can compare the momentum of ball A and ball B:
pA:pB=2mv:2mv
- This simplifies to:
pA:pB=1:1
The momentum of ball A is equal to the momentum of ball B. Therefore, the ratio of their momenta is 1:1.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - ICSECHAPTER - LAWS OF MOTIONEXERCISE - TOPIC 3 (2 Marks Questions )
9 Videos
- LAWS OF MOTIONBOOK - ICSECHAPTER - LAWS OF MOTIONEXERCISE - TOPIC 3 (3 Marks Questions )
7 Videos
- LAWS OF MOTIONBOOK - ICSECHAPTER - LAWS OF MOTIONEXERCISE - TOPIC 2 (3 Marks Questions )
11 Videos
- ICSE ANNUAL EXAMINATION -2020BOOK - ICSECHAPTER - ICSE ANNUAL EXAMINATION -2020EXERCISE - SECTION-II
45 Videos
- LIGHTBOOK - ICSECHAPTER - LIGHTEXERCISE - TOPIC 2 Spherical Mirrors (4 Marks Questions )
9 Videos
Similar Questions
Two balls A and B of masses m and 2 m are in motion with velocities 2v and v, respectively. Compare: Their inertia.
View SolutionTwo balls A and B of masses m and 2 m are in motion with velocities 2v and v, respectively. Compare: The force needed to stop them in the same
View SolutionTwo bodies A and B of same mass are moving with velocities v and 2v, respectively. Compare their momentum.
View SolutionTwo bodies A and B of same mass are moving with velocities v and 2v, respectively. Compare their inertia
View SolutionTwo particles, A and B of masses m and 3m, are moving along X and Y axes respectively, with the same speed v. They collide at the origin, and coalesce into one body, after the c ollision. What is the velocity of this coalesced mass ?
View SolutionTwo particles of masses m1 and m2 in projectile motion have velocities →v1 and →v2 , respectively , at time t=0. They collide at time t0. Their velocities become →v'1 and →v'2 at time 2t0 while still moving in air. The value of ∣∣∣(m1→v'1+m2→v'2)−(m1→v1+m2→v2)∣∣∣
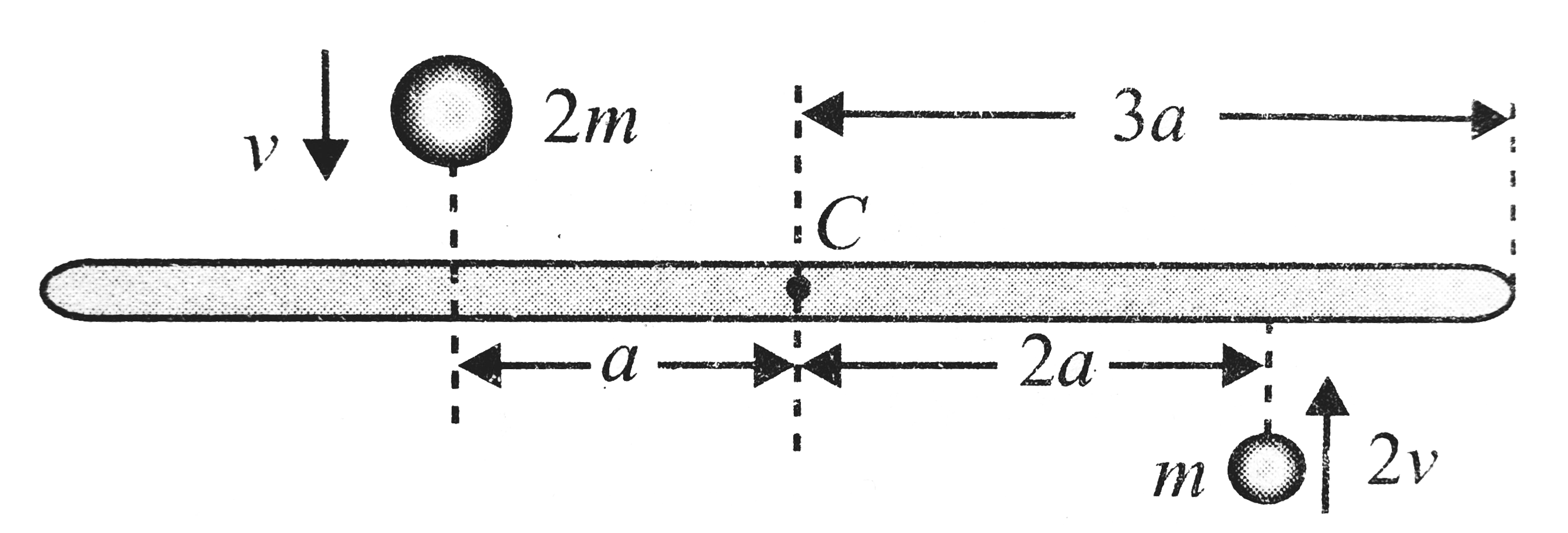
View SolutionA uniform bar of length 6a and mass 8m lies on a smooth horizontal table. Two point masses m and 2m moving in the same horizontal plane with speeds 2v and v, respectively, strike the bar (as shown in the figure) and stick to the bar after collision. Denoting angular velocity (about the centre of mass), total energy and centre of mass velocity by ω, E and VC, respectively, we have after collision
View SolutionTwo cars of same mass are moving with velocities v1andv2 respectively. If they are stopped by supplying same breaking power in time t1andt2 respectively then v1v2 is
View SolutionTwo particles of masses m and 2m moving in opposite directions collide elastically with velocity 2v and v, respectiely. Find their velocities after collision.

View SolutionTwo blocks A and B of mass m and 2m respectively are moving towards a massive (mass>>2m) cliff with velocities 2v and v respectively. The cliff moves with a velocity v. If the coefficient of restitution of collision at the surface of the cliff is e=1/2, find the:

a. velocity of the block B just after colliding with the cliff.
b. work done by the cliff during collision.
c. maximum compression of the spring of stiffness k which is fitted with the block B.
View Solution
