Two blocks A and B of masses m and 2m respectively are placed on a smooth floor. They are connected by a spring. A third block C of mass m moves with a velocity along the line joing A and B and collides elastically with A, as shown in figure. At a certain instant of time after collision, it is found that the instantaneous velocities of A and B are the same. Further, at this instant the compression of the spring is found to be . Determine (i) the common velocity of A and B at time , and (ii) the spring constant.
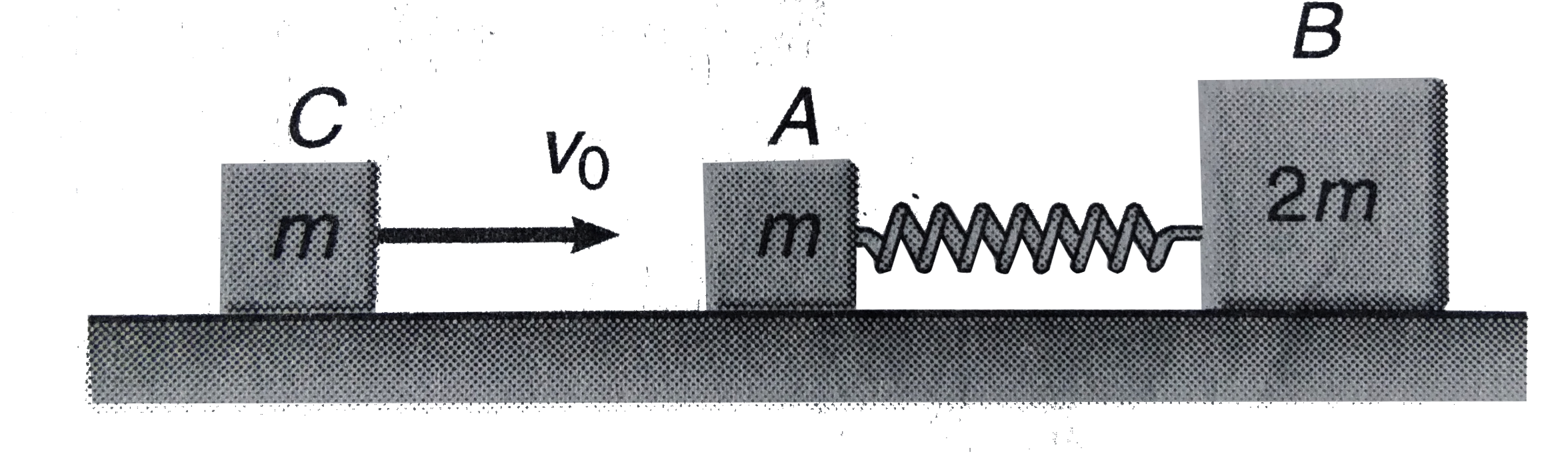
The correct Answer is:B, C
Initially, the blocks A and B are at rest and C is moving with velocity to the right. As masses of C and A are same and the collision is elastic the body C treansfers its whole momentum to body A and as a result the body C stops and A starts moving with velocity to the right. As this instant the spring is uncompressed and the body B is still at rest.
The momentum of the system at this instant
Now, the spring is compressed and the body B comes in motion. After time , the compression of the spring is and common velocity of A and B is v(say).
As external force on the system is zero, the law of conservation of linear momentum gives
or
The law of conservation of energy gives
or
or
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Exercise 11.113videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Exercise 11.26videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Solved Examples13videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions15videos
CENTRE OF MASS, IMPULSE AND MOMENTUM
- BOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery19videos
CIRCULAR MOTION
Similar Questions
Two blocks A and B of masses in and 2m respectively placed on a smooth floor are connected by a spring. A third body C of mass m moves with velocity v0 along the line joining A and B and collides elastically with A. At a certain instant of time after collision it is found that the instantaneous velocities of A and B are same then:
 View Solution
View SolutionTwo bodies A and B of masses m and 2m respectively are placed on a smooth floor. They are connected by a light spring of stiffness k.
A third body C of mass m moves with velocity v0 along the line joining A and B and collides elastically with A. If lo be the natural length of the spring then find the minimum separation between the blocks.
 View Solution
View SolutionA ball A of mass M collides elastically with a similar ball B at rest as shown in figure. Initially velocity of ball A is u m/s. After collision,
 View Solution
View SolutionA body of mass m2 moving with velocity v0 collides elastically with another mass of m3 . Find % change in KE of first body
View SolutionA heavy ball of mass 2M moving with a velocity v0 collides elastically head on with a cradle of three identical ball each of mass M as shown in figure. Determine the velocity of each ball after collision.
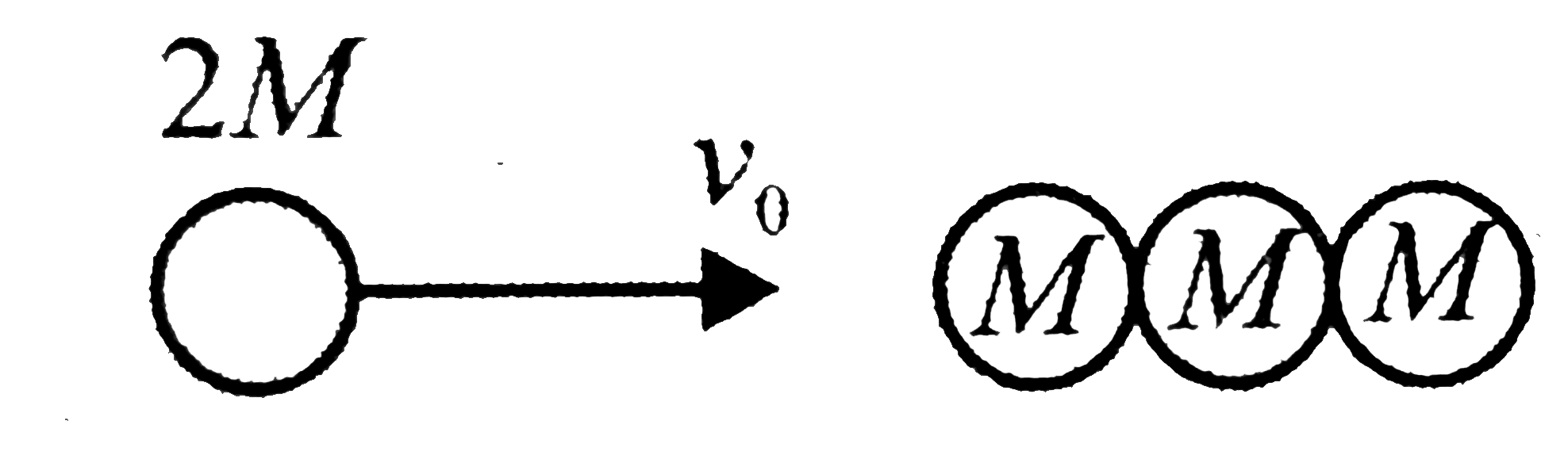 View Solution
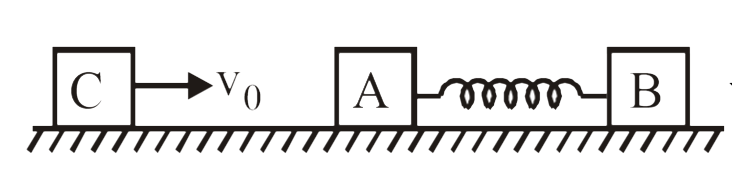
View SolutionA block C of mass m is moving with velocity v0 and collides elastically with block A of mass m and connected to another block B of mass 2m through spring constant k. What is k if x0 is compression of spring when velocity of A and B is same?
 View Solution
View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. The maximum compression in spring is
 View Solution
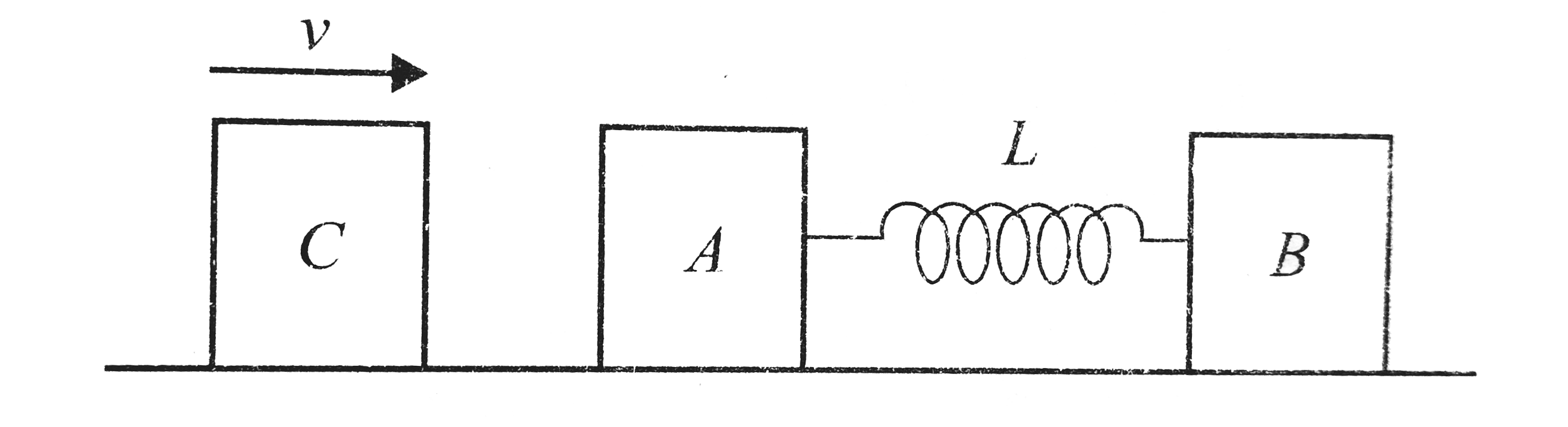
View SolutionTwo blocks A and B. each of mass m, are connected by a massless spring of natural length I. and spring constant K. The blocks are initially resting in a smooth horizontal floor with the spring at its natural length, as shown in Fig. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A and B. and collides elastically with A. Then
 View Solution
View SolutionTwo blocks A and B of mass 2m and m respectively are connected to a massless spring of force constant K as shown in figure A and B are moving on the horizontal frcitionless surface with velocity v to right with underformed spring. If B collides with C elastically, then maximum compression of the spring will be
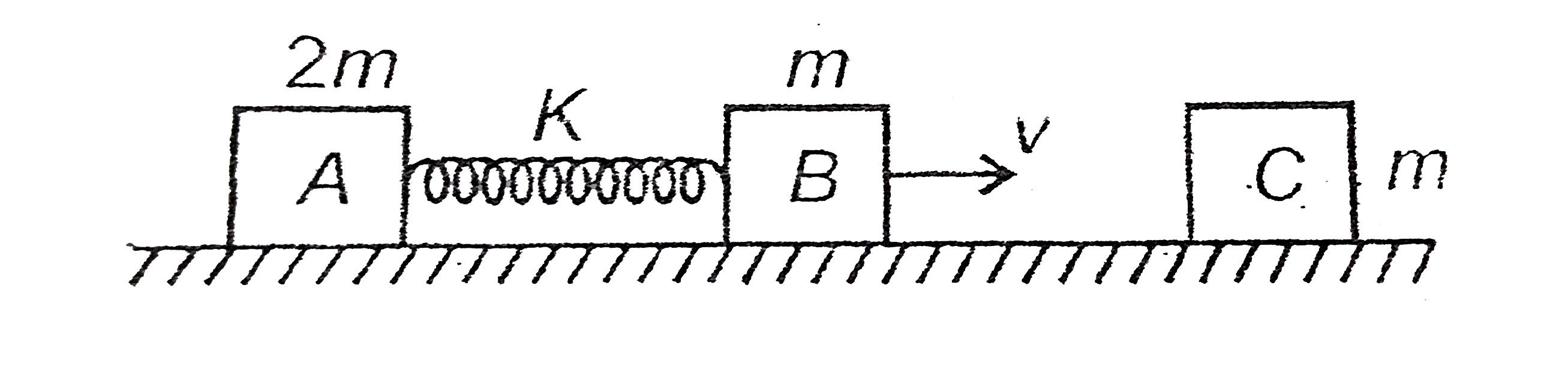 View Solution
View SolutionTwo blocks A and B of masses m and 2m, respectively are connected by a spring of force constant k. The masses are moving to the right with uniform velocity v each, the heavier mass leading the lighter one. The spring is in the natural length during this motion. Block B collides head on with a third block C of mass m, at rest, the collision being completely inelastic. Calculate the maximum compression of the spring.
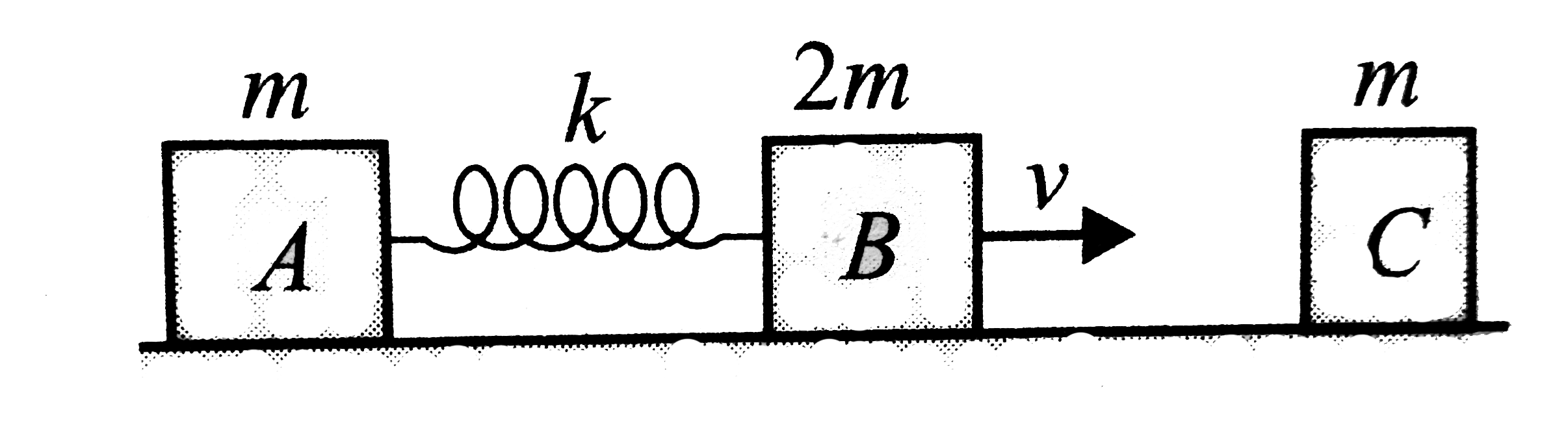 View Solution
View Solution
