Two blocks are connected by a string, as shown in figure. They are released from rest. Show that after they have moved a distance L, their common speed is given by v=√2(m2−μm1)gL/(m1+m2), in which μ is the coefficient of kinetic friction between the upper block and the surface. Assume that the pulley is massless and frictionless.
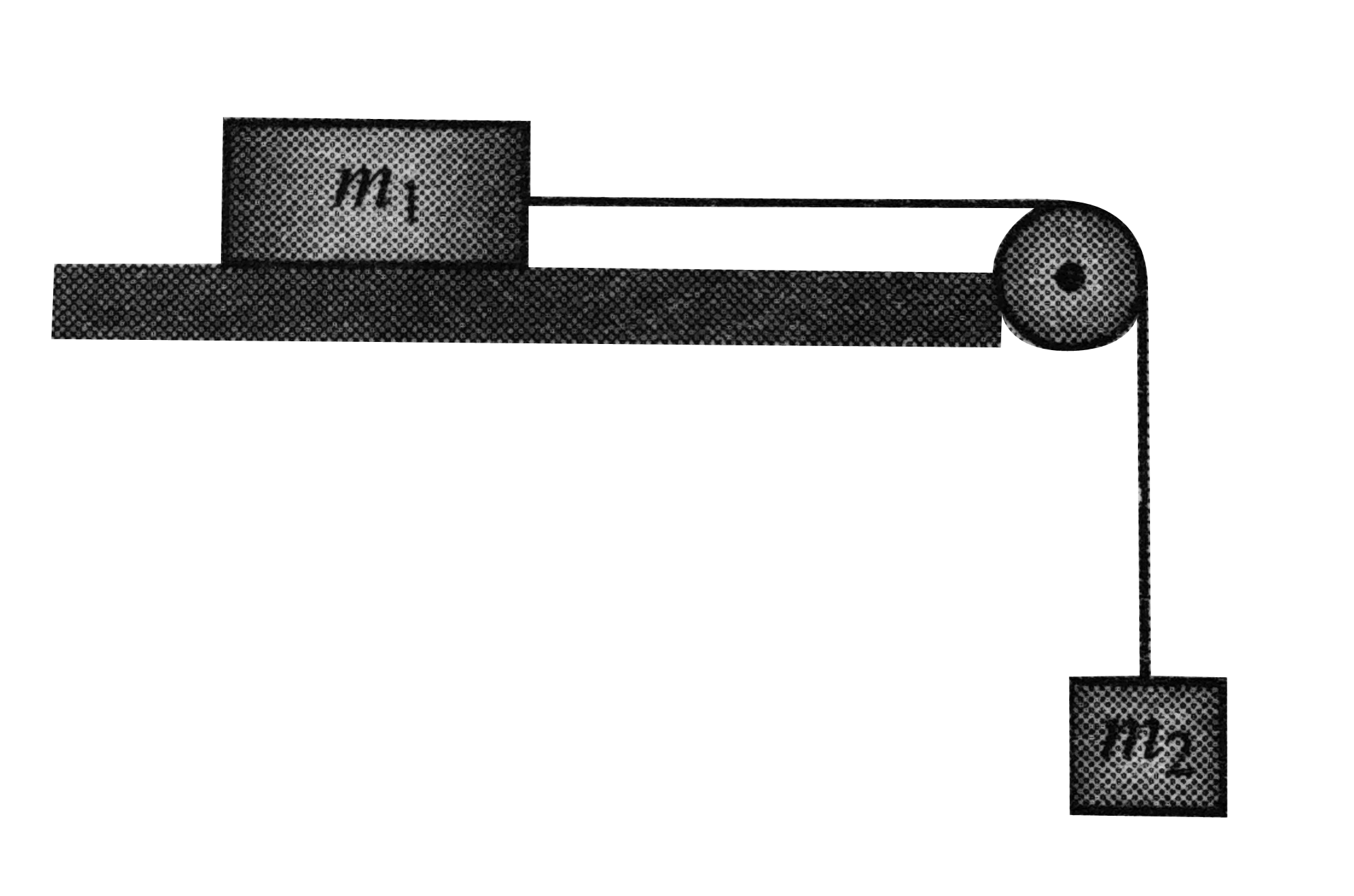
First we will solve the problem by the force method and then by the work-energy method. This will give you an opportunity to compare these two methods and sharpen your skills in selecting the method to be used for solving a prolem.
Force method: Let the acceleration of m1 be a horizontally towards right. The acceleration of m2 will be a vertically downwards (pulley constraint). Application of ∑→F=m→a to m1 and m2 (see the free body diagrams for m1 and m2 in figure shows
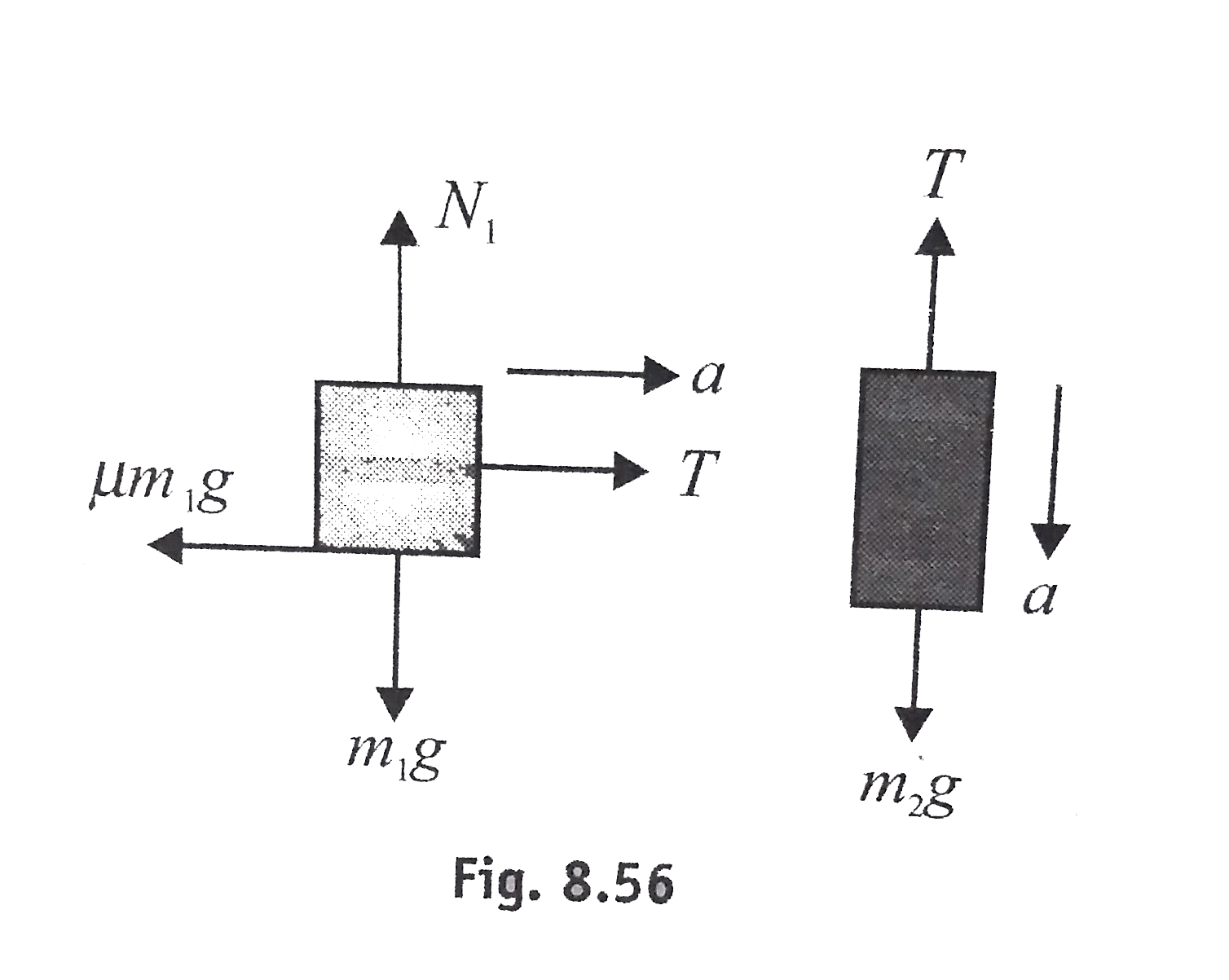
T−μm1g=m1a and m2g−T=m2a
Solving these equations for a, we get a=(m2−μm1)m1+m2g
Using s=ut+(1/2)at2, we find that the blocks take time.
t=√2L(m1+m2)(m2−μm1)g
to cover the ditance L, and from v=u+at, they will have the speed
v=0+(m2−μm1)gm1+m2×√2L(m1+m2)g(m2−μm1)g
=√2Lg(m2−μm1)m2+m1
Work-energy method: The essence of the process in terms of energy considerations is that m2 loses potential energy of amount m2gL while coming down by L, and the loss of potential energy of m2 appears partly in m1 and m2 in the form of kinetic energy and is partly used up as as work done against friction.
m2gL=12(m1+m2)v2+μm1gL
⇒(m2−μm1)gL=12(m1+m2)v2
⇒v=√2(m2−μm1)gLm1+m2
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Solved Examples
15 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.1
25 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
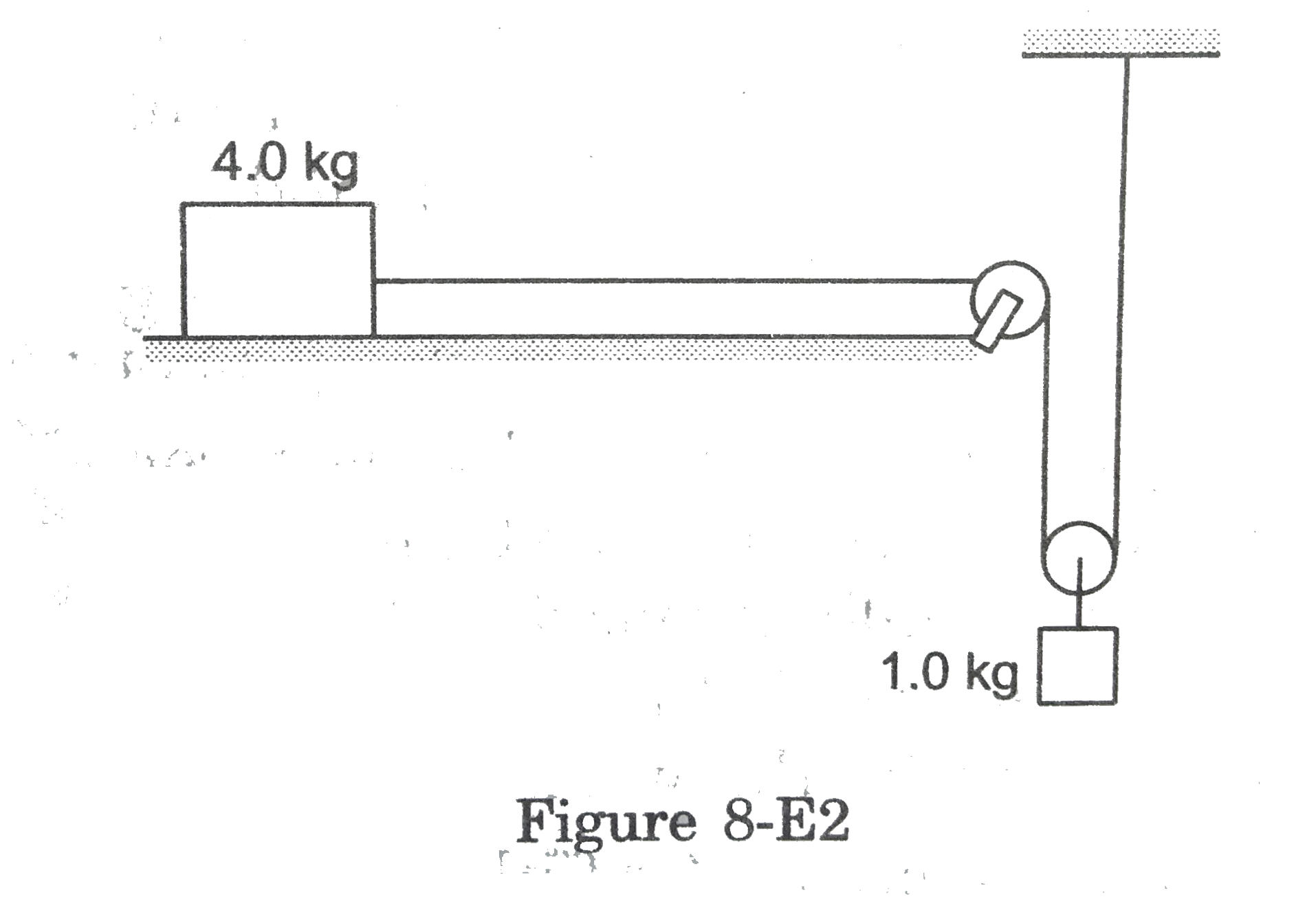
Consider the situatioin shown in figure. The system is released from rest and the block of mass 1.0 kg is found to have a speed 0.3 m/s ater it has descended thrugh a distance of 1 m. find the coefficient of kinetic friction between the block and the table.
View Solution
Consider a situation as shown in the figure. The system is released from rest. When the block of mass m has falled a distance L, its speed becomes √gL3. Find the friction coefficient μ.
View Solution
Knowledge Check

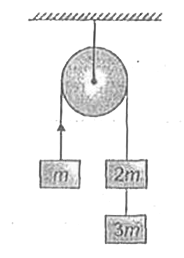
Two blocks of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is :Am2gm1+m2Bm1gm1+m2C4m2g−m1gm1+m2Dm2gm1+4m2In the figure given below, with what accelerating does the block of mass m will move? ( Pulley and strings are massless and frictionless)
Ag3B2g5C2g3Dg2Two block of masses M and m are connected to each other by a massless string and spring of force constant k as shown in the figure. The spring passes over a frictionless pulley connected rigidly to the egde of a stationary block A. The coefficient of friction between block M and plane horizontal surface of A is μ. The block M slides over the horizontal top surface of A and block m slides vertically downward with the same speed. The mass M is equal to
 AmμB2mμCmμDμmg
AmμB2mμCmμDμmg
In the figure given below, with what acceleration does the block of mass m will move? (Pulley and strings are massless and frictionless)
View SolutionWhen the three blocks in Fig. 6-45 are released from rest, they accelerate with a magnitude of 0.500 m/s2 Block 1 has mass M, block 2 has 2M, and block 3 has 2M. What is the coefficient of kinetic friction between block 2 and the table?
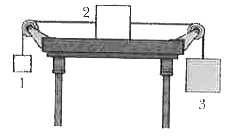
View SolutionFind the relation between acceleration of the two blocks m1andm2. Assume pulleys are massless and frictionless and the strings are inextensible .
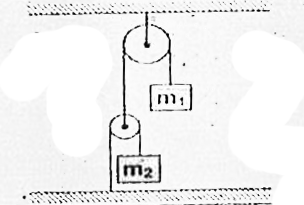
View SolutionA block of mass m = 2kg is accelerating by a force F = 20N applied on a smooth light pulley as shown in the figure. If the coefficient of kinetic friction between the block and the surface is μ=0.3, find its acceleration.
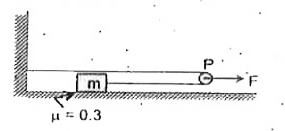
View SolutionWhen the three blocks of masses M, 2M and 2M in the system are released from rest, they accelerate with a magnitude of 1 m/s2. What is the coefficient of kinetic friction between block on the table and the table top? (neglect the force of friction in the pulleys and take g =10 m/s2)
View Solution
