Two blocks each of mass M are connected to the ends of a light frame as shown in figure. The frame si rotated about the vertical line of symmetry. The rod breaks if the tension in it exceeds T0. Find the maximum frequency with which the frame may be rotted without breaking the rod.

12π(To2Ml)1/2
14π(ToMl)1/2
12π(ToMl)1/2
14(ToMl)1/2
The correct Answer is:C
Consider one of the blocks if the frequency of revolution is f, the angular velocity is ω=2πf. The acceleration towards the centre is
v2l=ω2l=4π2f2l.
The only only horizontal force on the block is the tension of the rod. at the point of breaking, this force is T0, so, from newton's laws.
T0=M⋅4π2⋅f2l
or f=12π(T∘Ml)1/2
Topper's Solved these Questions
Similar Questions
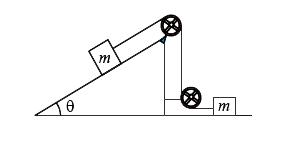
Two blocks each of mass m are connected over two light and frictionless pulleys and a fixed wedge by a light string as shown in figure. The tension in the string is :
View SolutionA body of mass m s connected to an inextensible thread of length L si whirled in horizontal circle. Find the maximum angular velocity with which it can be whirsted without breaking the thread (Breaking stress of thread =S)
View Solution
Knowledge Check
A particle of mass 100 g tied to a string is rotated along the circle of radius 0.5 m. The breaking tension of the string is 10 N. The maximum speed with which particle can be rotated without breaking the string is
A10 ms−1B9.8m s−1C7.7 m s−1D7.07 m s−1Two blocks each of the mass m are attached to the ends of a massless rod which pivots as shown in figure. Initially the rod is held in the horizontal position and then released. Calculate the initial angular acceleration.
 A(l2−l1)gl21+l22 clockwiseB(l2+l1)g(l22+l21) clockwiseC(l2−l1)g2(l22+l21) clockwiseDgl2+l1 clockwise
A(l2−l1)gl21+l22 clockwiseB(l2+l1)g(l22+l21) clockwiseC(l2−l1)g2(l22+l21) clockwiseDgl2+l1 clockwiseTwo blocks each of the mass m are attached to the ends, a massless rod which pivots as shown in figure. Initial the rod is held in the horizontal position and then release, Calculate the net torque on this system above pivot.
 A(ml2g−ml1g)ˆkB(ml1g−ml2g)ˆkC(ml1g+ml2g)ˆkD−(ml1g+ml2g)ˆk
A(ml2g−ml1g)ˆkB(ml1g−ml2g)ˆkC(ml1g+ml2g)ˆkD−(ml1g+ml2g)ˆk
A uniform rod of mass m and length L is fixed to an axis, making an angle θ with it as shown in the figure. The rod is rotated about this axis so that the free end of the rod moves with a uniform speed ‘v’. Find the angular momentum of the rod about the axis. Is the angular momentum of the rod about point A constant?

View SolutionTwo identical uniform rods AB and CD, each of length L are jointed to form a T-shaped frame as sown in figure. Locate the centre of mass of the frame. The centre of mass of a uniform rod is at the middle point of the rod.

View SolutionA block of mass m is connected to a spring of spring constant k as shown in figure. The frame in which the block is placed is given an acceleration a towards left. Neglect friction between the block and the frame walls. The maximum velocity of the block relative to the frame is

View SolutionA uniform rod of mass m and length l is fixed from Point A, which is at a distance l/4 from one end as shown in the figure. The rod is free to rotate in a vertical plane. The rod is released from the horizontal position.

What is the reaction at the hinge, when kinetic energy of the rod is maximum?
View SolutionFor identical rods each of mass m and length l make a square frame in xy plane as shown. Calculate its momen of inertia about the x-axis.
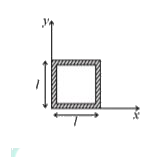
View Solution
