Two blocks of equal mass m are connected by an unstretched spring and the system is kept at rest on a frictionless horizontal surface. A constant force F is applied on one of the blocks pulling it away from the other as shown in figure. (a) Find the displacement of the centre of mass at time t. (b) If the extension of the spring is x0 at time t, find the displacement of the two blocks at this instant.

The correct Answer is:A, B
(a) The acceleration of the centre of mass is
aCOM=F2m
The displacement of the centre of mass at time t will be
x=12aCOM t2=Ft24m
(b) Suppose the displacement of the first block is x1 and that of the second is x2. Then,
x=mx1+mx22m or Ft24m=x1+x22
or x1+x2=Ft22m ...(i)
Further, the extension of the spring is x1−x2. Therefore,
x1−x2=x0
From Eqs. (i) and (ii),
x1=12(Ft22m+x0) and x2=12((Ft)22m−x0)
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Exercise 11.1
13 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Exercise 11.2
6 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Solved Examples
13 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
Two block of equal mass m are connected by an unstretched spring and the sytem is kept at rest on a frictionless horizontal surface. A constant force F is applied on one of the blocks puling it away from the other as shown in figure. a.Find the positon of the centre of mass at time t. b.If the extansion of the spring is x0 at time t find the displacement of the two blocks at this instant.
View SolutionTwo blocks of equal mass m are connected by an unstretched spring and the system is kept at rest on a frictionless horizontal surface. A constant force F is applied on the first block pulling away from the other as shown in Fig.

Then the displacement of the centre of mass in at time t is
View SolutionTwo blocks each of mass m, connected by an un-stretched spring are kept at rest on a frictionless horizontal surface. A constant force F is applied on one of the blocks pulling it away from the other as shown in figure.
(a)Find accelaration of the mass center.
(b) Find the displacement of the centre of mass as function of time t.
(c) If the extension of the spring is X0 at an instant t, find the displacements of the two blocks relative to the ground at this instant.
View SolutionTwo blocks of equal mass m are connected by an unstretched spring and the system is kept at rest on a frictionless horizontal surface. A constant force F is applied on the first block pulling away from the other as shown in Fig.

If the extension of the spring is x0 at time t, then the displacement of the first block at this instant is
View SolutionTwo blocks of equal mass m are connected by an unstretched spring and the system is kept at rest on a frictionless horizontal surface. A constant force F is applied on the first block pulling away from the other as shown in Fig.

If the extension of the spring is x0 at time t, then the displacement of the first block at this instant is
View SolutionTwo blocks of masses M1andM2 are placed in contact with each other on a frictionless horizontal surface. If a force F is applied on the block of mass M1, what is the contact force between the two blocks?
View SolutionTwo identical blocks A and B each of mass M are connected to each other through a light string. The system is placed on a smooth horizontal floor. When a constant force F is applied horizontally on the block A, find the tension in the string.
View SolutionAssertion: A constant force F is applied on two blocks and one spring system as shown in figure. Velocity of centre of mass increases linearly with time.

Reason: Acceleration of centre of mass is constant.
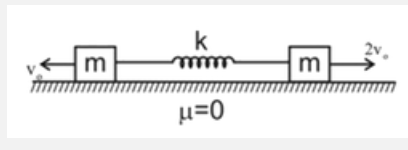
View SolutionThe figure shows two blocks of mass m each, connected by an ideal unstretched spring and then placed on a frictionless floor. If the blocks are given velocities v0and2v0 as shown, then the maximum extension in the spring is
View SolutionTwo blocks of masses m1 and m2 are connected by an ideal sprit, of force constant k. The blocks are placed on smooth horizontal surface. A horizontal force F acts on the block m1. Initially spring is relaxed, both the blocks are at rest.

What is acceleration of centre of mass of system at the instant of maximum elongation of spring
View Solution
