Two blocks of masses m and M connected by a light spring of stiffness k, are kept on a smooth horizontal surface as shown in figure. What should be the initial compression of the spring so that the system will be about to break off the surface, after releasing the block m1?
To solve the problem, we need to determine the initial compression of the spring so that the system will be about to break off the surface after releasing the block of mass m.
1. Understand the Forces Acting on the Blocks:
- The block of mass m is connected to the block of mass M by a spring with spring constant k.
- When the spring is compressed by an amount x, it exerts a force on both blocks.
2. Determine the Force Required for Each Block to Lift Off the Surface:
- For the block of mass m to just lift off the surface, the spring force must equal the weight of the block.
- The spring force F exerted by the spring when compressed by x1 is given by:
F=k⋅x1
- Setting this equal to the weight of block m:
k⋅x1=m⋅g
- From this, we can solve for x1:
x1=m⋅gk
3. Repeat for the Block of Mass M:
- Similarly, for the block of mass M to just lift off, the spring force when compressed by x2 must equal the weight of block M:
k⋅x2=M⋅g
- Solving for x2:
x2=M⋅gk
4. Calculate Total Compression of the Spring:
- The total initial compression x of the spring when both blocks are compressed is the sum of the individual compressions:
x=x1+x2
- Substituting the values we found:
x=m⋅gk+M⋅gk
- This simplifies to:
x=(m+M)⋅gk
5. Final Result:
- The initial compression of the spring required for the system to just break off the surface after releasing the block m is:
x=(m+M)⋅gk
- The block of mass m is connected to the block of mass M by a spring with spring constant k.
- When the spring is compressed by an amount x, it exerts a force on both blocks.
- For the block of mass m to just lift off the surface, the spring force must equal the weight of the block.
- The spring force F exerted by the spring when compressed by x1 is given by:
F=k⋅x1
- Setting this equal to the weight of block m:
k⋅x1=m⋅g
- From this, we can solve for x1:
x1=m⋅gk
- Similarly, for the block of mass M to just lift off, the spring force when compressed by x2 must equal the weight of block M:
k⋅x2=M⋅g
- Solving for x2:
x2=M⋅gk
- The total initial compression x of the spring when both blocks are compressed is the sum of the individual compressions:
x=x1+x2
- Substituting the values we found:
x=m⋅gk+M⋅gk
- This simplifies to:
x=(m+M)⋅gk
- The initial compression of the spring required for the system to just break off the surface after releasing the block m is:
x=(m+M)⋅gk
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Solved Examples15videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.125videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
Similar Questions
Two blocks of masses m1 and m2, connected by a weightless spring of stiffness k rest on a smooth horizontal plane as shown in Fig. Block 2 is shifted a small distance x to the left and then released. Find the velocity of centre of mass of the system after block 1 breaks off the wall.
 View Solution
View SolutionTwo bars of masses m1 and m2 connected by a weightless spring of stiffness k, rest on a smooth horizontal plane. Bar 2 is shifted by a small distance x0 to the left and released. The veloicyt of the centre of mass of the system when bar 1 breaks off the wall is
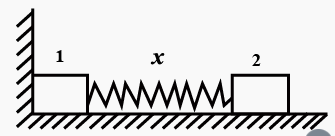 View Solution
View SolutionChoose the correct option:
Two bars of masses m1 and m2 connected by a weightless spring of stiffness k, rest on a smooth horizontal plane. Bar 2 is shifted by a small distance x0 to the left and released. The velocity of the centre of mass of the system when bar 1 breaks off the wall is
 View Solution
View SolutionTwo blocks of masses m1andm2 being connected with a light spring of stiffness k are driven with forces F1andF2 on a smooth plane .find the value of spring force .
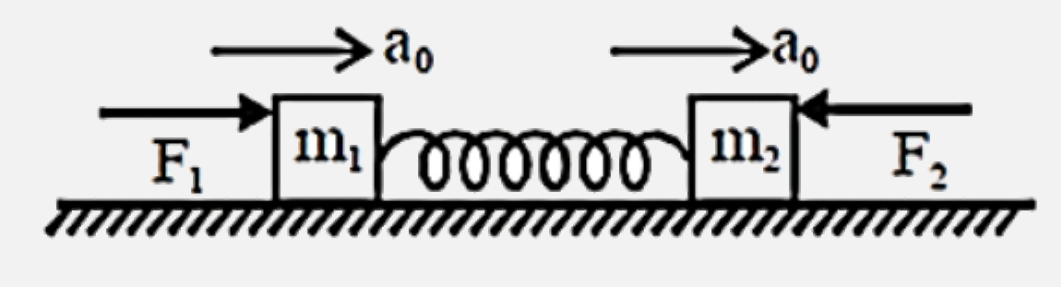 View Solution
View SolutionA block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released
 View Solution
View SolutionTwo blocks of masses m1 and m2 are connected by a massless spring and placed on smooth surface. The spring initially stretched and released. Then :
View SolutionTwo blocks of masses m and m' are connected by a light spring on a horizontal frictionless table . The spring is compressed and then released . Find the ratio of acceleration of masses .
View SolutionTwo smooth blocks of mases m1andm2 attached with an ideal spring of stiffness k and kept on hrozontal surface. If m1 is projected with a horizontal velocity v0. Find the maximum compression of the spring.
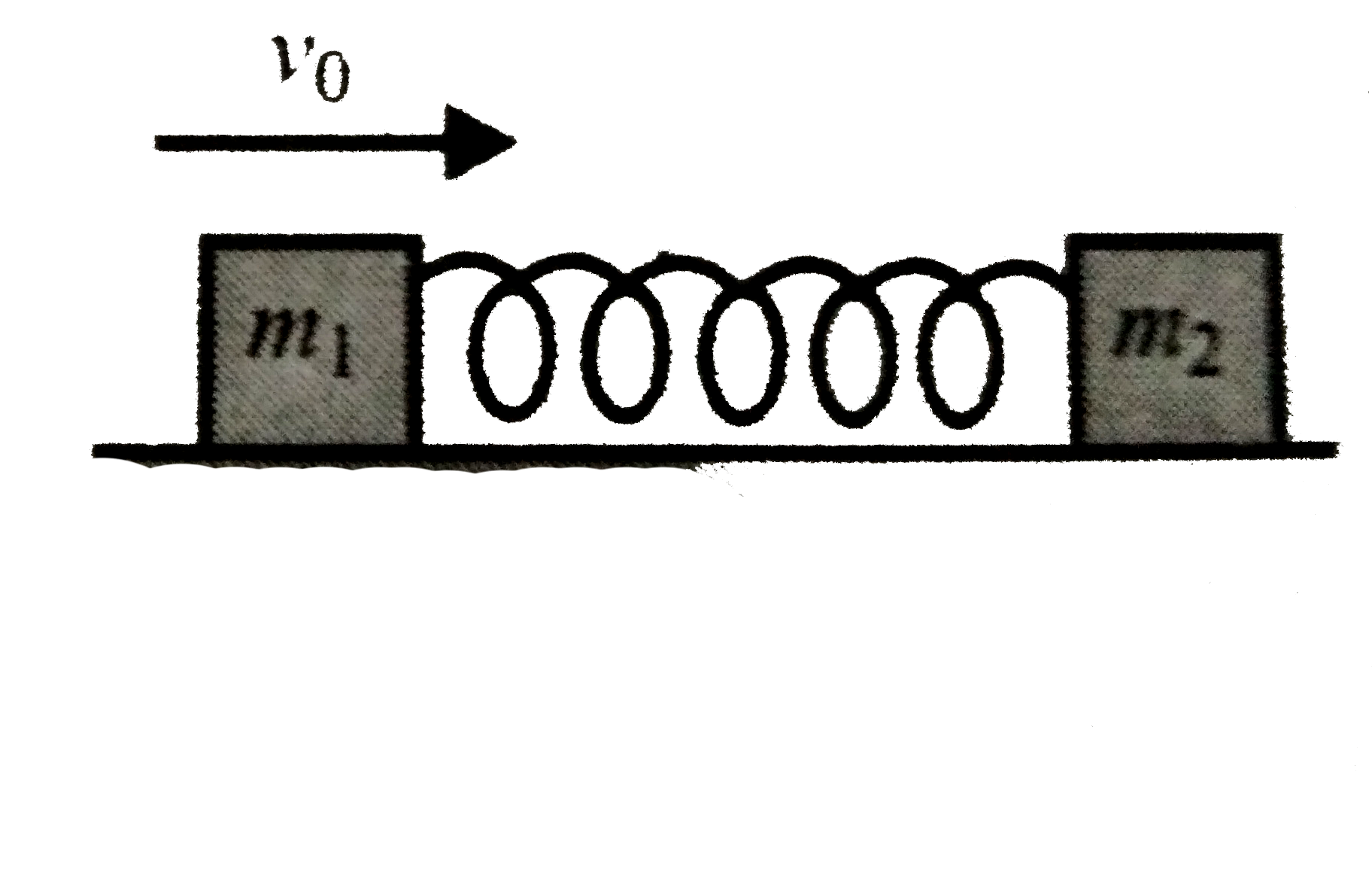 View Solution
View SolutionTwo blocks of masses m1 and m2 interconnect with a spring of stiffness K, are kept on as smooth horizontal surface. Find out the ratio of velocity, displacement, kinetic energy and acceleration block with mass m1 of block with mass m2.
View SolutionA block of mass m compresses a spring iof stifffness k through a distacne l/2 as shown in the figure .If the block is not fixed to the spring the period of motion of the block is
 View Solution
View Solution

