Two blocks of steel A and B, A being two times heavier than B, are at 40∘C. The ratio of heat content of A to B is
1
4
2
12
The correct Answer is:C
To find the ratio of heat content of two blocks of steel A and B, we can follow these steps:
Step 1: Define the Mass of Each Block
Let the mass of block B be m. Since block A is two times heavier than block B, we can express the mass of block A as:
Mass of A=2m
Step 2: Define the Specific Heat Capacity
Both blocks are made of steel, which means they have the same specific heat capacity. Let the specific heat capacity of both blocks be S.
Step 3: Calculate the Heat Content of Each Block
The heat content (or heat capacity) of an object can be calculated using the formula:
Heat Content=Mass×Specific Heat Capacity×Temperature
Since both blocks are at the same temperature (40∘C), we can ignore the temperature in the ratio calculation.
For block A, the heat content QA is:
QA=Mass of A×S=(2m)×S=2mS
For block B, the heat content QB is:
QB=Mass of B×S=m×S=mS
Step 4: Calculate the Ratio of Heat Content
Now, we can find the ratio of the heat content of block A to block B:
Ratio=QAQB=2mSmS
When we simplify this, we find:
Ratio=2mSmS=2
Conclusion
The ratio of the heat content of block A to block B is:
Ratio=2
Let the mass of block B be m. Since block A is two times heavier than block B, we can express the mass of block A as:
Mass of A=2m
Both blocks are made of steel, which means they have the same specific heat capacity. Let the specific heat capacity of both blocks be S.
The heat content (or heat capacity) of an object can be calculated using the formula:
Heat Content=Mass×Specific Heat Capacity×Temperature
Since both blocks are at the same temperature (40∘C), we can ignore the temperature in the ratio calculation.
QA=Mass of A×S=(2m)×S=2mS
QB=Mass of B×S=m×S=mS
Now, we can find the ratio of the heat content of block A to block B:
Ratio=QAQB=2mSmS
When we simplify this, we find:
Ratio=2mSmS=2
The ratio of the heat content of block A to block B is:
Ratio=2
Topper's Solved these Questions
- HEATBOOK - MCGROW HILL PUBLICATIONCHAPTER - HEATEXERCISE - HIGHER ORDER THINKING QUESTIONS
15 Videos
- GRAVITATION BOOK - MCGROW HILL PUBLICATIONCHAPTER - GRAVITATION EXERCISE - HIGHER ORDER THINKING QUESTIONS
25 Videos
- HEATING AND MAGNETIC EFFECTS OF CURRENT BOOK - MCGROW HILL PUBLICATIONCHAPTER - HEATING AND MAGNETIC EFFECTS OF CURRENT EXERCISE - HIGHER ORDER THINKING QUESTIONS
34 Videos
Similar Questions
A block A slides over an another block B which is placed over a smooth inclined plane as shown in figure . The coefficient of friction between the two blocks A and B is μ . Mass of block B is two times the mass of block A . The acceleration of the centre of mass of two blocks is
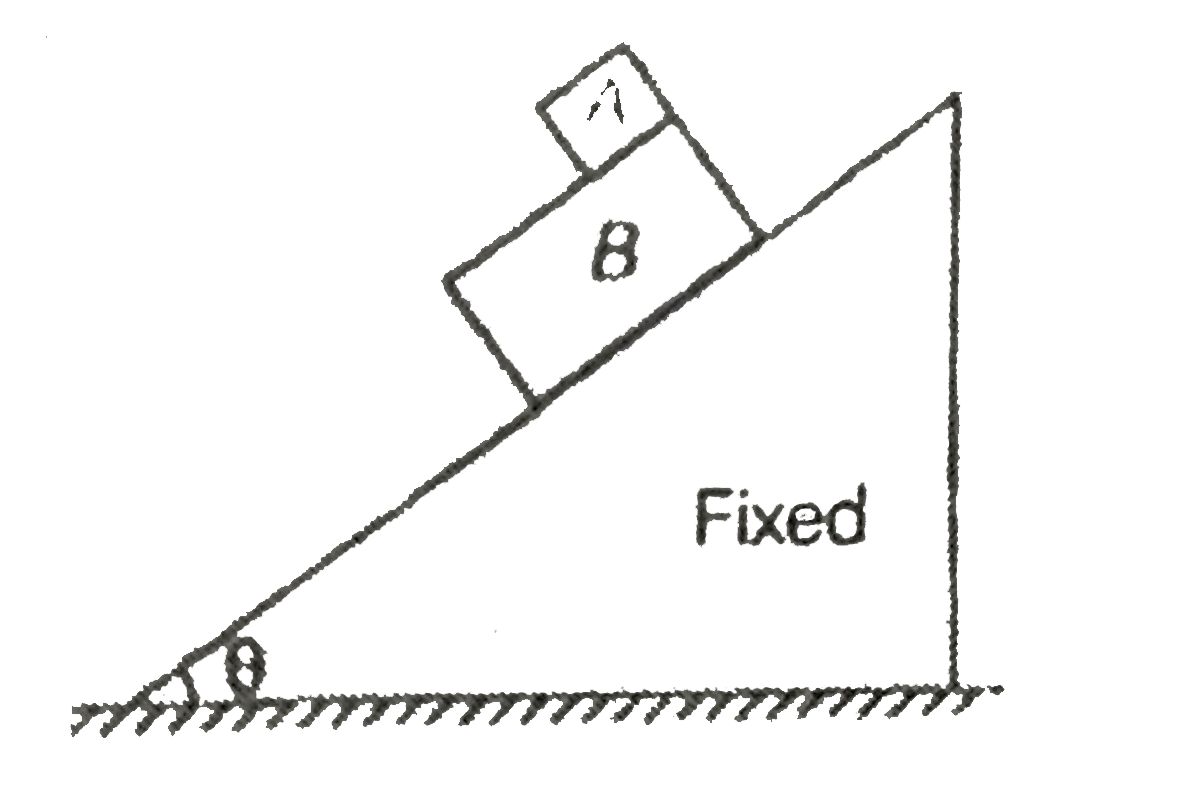
View SolutionTwo vessels separately contain two ideal gases A and B at the same temperature, the pressure of A being twice that of B. Under such conditions, the density of A is found to be 1.5 times the density of B. The ratio of molecular weight of A and B is
View Solution
Knowledge Check
Two block of lead ,one twice as heavy as the other are at 50∘–– C.The ratio of heat content of the heavier block to that of the lighter block is
A0.5B1C2D4Two blocks of metal, one twice as heavy as the other, are both at 60∘C. The ratio of the heat energy of the heavier block to that of the lighter block is
A0.5B1C2D4Helium atom is two times heavier than hydrogen molecule. At 25∘C, the kinetic energy of He atom is
ADouble than hydrogenBSame than hydrogenCFour times than hydrogenDHalf than hydrogen
A block A slides over another block B which is placed over a smooth inclined plane. The coefficient of friction between the two blocks. A and B is μ. Mass of block B is two times the mass of block A. The acceleration of the centre of mass of two blocks is
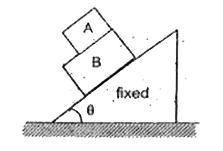
View SolutionTwo wires A and B have the same length and area of cross-section. But Young's modulus of A is two times the Young's modulus of B. Then the ratio of force constant of A to that of B is
View SolutionTwo wires A and B have the same length and area of cross-secton. But Young's modulus of A is two times the Young's modulus of B. Then the ratio of force constant of A to that of B is
View SolutionTransverse waves of same frequency are generated in two steel wires A and B . The diameter of A is twice of B and the tension in A is half that in B. The ratio of velocities of wave in A and B is
View SolutionThe ratio of speeds of A is to B is 2:3 and therefore A takes 20 minutes more time than B takes.What is the time taken by A and B ?
View Solution
