Two capacitors of unknown capacitance are connected in series and parallel. The effective capacitance in series and parallel combination are 4 μF to 18μF, respectively . Find the capacitance of unknown capacitors.
To find the capacitance of the unknown capacitors C1 and C2 given their effective capacitance in series and parallel, we can follow these steps:
Step 1: Write the equations for series and parallel combinations
For capacitors in series, the effective capacitance Cs is given by:
1Cs=1C1+1C2
For the given problem, Cs=4μF:
14=1C1+1C2(1)
For capacitors in parallel, the effective capacitance Cp is given by:
Cp=C1+C2
For the given problem, Cp=18μF:
C1+C2=18(2)
Step 2: Rearranging equation (1)
From equation (1), we can express C2 in terms of C1:
1C2=14−1C1
Taking the reciprocal gives:
C2=4C1C1−4(3)
Step 3: Substitute equation (3) into equation (2)
Now, substitute C2 from equation (3) into equation (2):
C1+4C1C1−4=18
To eliminate the fraction, multiply through by C1−4:
C1(C1−4)+4C1=18(C1−4)
Expanding both sides:
C21−4C1+4C1=18C1−72
This simplifies to:
C21−18C1+72=0(4)
Step 4: Solve the quadratic equation (4)
We can solve the quadratic equation using the quadratic formula:
C1=−b±√b2−4ac2a
Here, a=1,b=−18,c=72:
C1=18±√(−18)2−4⋅1⋅722⋅1
Calculating the discriminant:
C1=18±√324−2882
C1=18±√362
C1=18±62
This gives two possible solutions:
C1=242=12orC1=122=6
Step 5: Find C2
Using equation (2) to find C2:
1. If C1=12:
C2=18−12=6
2. If C1=6:
C2=18−6=12
Conclusion
The capacitances of the unknown capacitors are:
C1=12μF,C2=6μFor vice versa.
For capacitors in series, the effective capacitance Cs is given by:
1Cs=1C1+1C2
For the given problem, Cs=4μF:
14=1C1+1C2(1)
Cp=C1+C2
For the given problem, Cp=18μF:
C1+C2=18(2)
From equation (1), we can express C2 in terms of C1:
1C2=14−1C1
Taking the reciprocal gives:
C2=4C1C1−4(3)
Now, substitute C2 from equation (3) into equation (2):
C1+4C1C1−4=18
To eliminate the fraction, multiply through by C1−4:
C1(C1−4)+4C1=18(C1−4)
Expanding both sides:
C21−4C1+4C1=18C1−72
This simplifies to:
C21−18C1+72=0(4)
We can solve the quadratic equation using the quadratic formula:
C1=−b±√b2−4ac2a
Here, a=1,b=−18,c=72:
C1=18±√(−18)2−4⋅1⋅722⋅1
Calculating the discriminant:
C1=18±√324−2882
C1=18±√362
C1=18±62
This gives two possible solutions:
C1=242=12orC1=122=6
Using equation (2) to find C2:
1. If C1=12:
C2=18−12=6
2. If C1=6:
C2=18−6=12
The capacitances of the unknown capacitors are:
C1=12μF,C2=6μFor vice versa.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Conceptual Questions
37 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Tough & Tricky PROBLEMS
10 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - PRACTICE PROBLEMS 4
7 Videos
- ELECTROMAGNETIC WAVESBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
16 Videos
Similar Questions
Knowledge Check
Two identical capacitors are first connected in series and then in parallel. The ratio of equivalent capacitance is
A1:1B1:2C1:3D1:4Six capacitors each of capacitance of 2μF are connected as shown in the figure. The effective capacitance between A and B is:
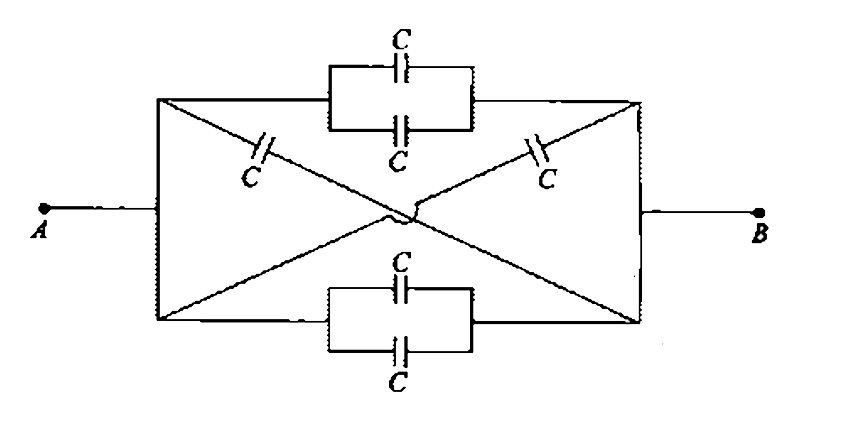 A12μFB8/3μFC3μFD6μF
A12μFB8/3μFC3μFD6μFTwo condensers each of 4μF capacitance are joined in parallel. The resultant capacitance of the combination is
A2μFB4μFC6μFD8μF
The effective capacitance between the points X and Y is
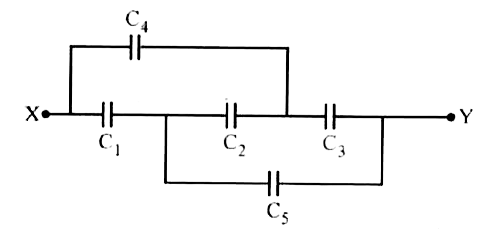
(all capacitor are of 4μF)
View Solution4.Three capacitors each of capacitance C are connected in series.Their equivalent capacitance will be ....................
View SolutionIf two capacitors 2μFand6μF are put in series. The effective capacitance of the system will be
View SolutionThree capacitors each of capacity 4μF are to be connected in such a way that the effective capacitance is 6μF. This can be done by
View SolutionTwo capacitors of capacitance C are connected in series. If one of them is filled with dielectric substance K, what is the effective capacitance?
View Solution
