Two cells of emfs epsilon(1)and epsilon(2) and internal resistances

Topper's Solved these Questions

BOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - REVISION EXERCISES (ADDITIONAL QUESTIONS)
11videos
CURRENT ELECTRICITY
BOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - REVISION EXERCISES (FILL IN THE BLANKS)
10videos
CURRENT ELECTRICITY
BOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - HIGHER ORDER THINKING SKILLS & ADVANCED LEVEL
10videos
CURRENT ELECTRICITY
BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test
16videos
ATOMS
BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15videos
DUAL NATURE OF RADIATION AND MATTER

Knowledge Check

Question 1 - Select One or More
Two batteris of emf $ε_{1}$ and $ε_{2}$ wit respective internal resistance $r_{1}$ and $r_{2}$ are connected in parallel. Now
AThe effective emf of this parallel combination is $\frac{(ε_{1} r_{1} + ε_{2} r_{2})}{(r_{1} + r_{2})}$
BThe effective internal resistance of this combination is $\frac{2 r_{1} r_{2}}{(r_{1} + r_{2})}$
Cthe effective emf of this parallel combination is $\frac{(ε_{1} r_{2} + ε_{2} r_{1})}{(r_{1} + r_{2})}$
DThe effective internal resistance of this combination is $\frac{r_{1} r_{2}}{(r_{1} + r_{2})}$
Question 2 - Select One

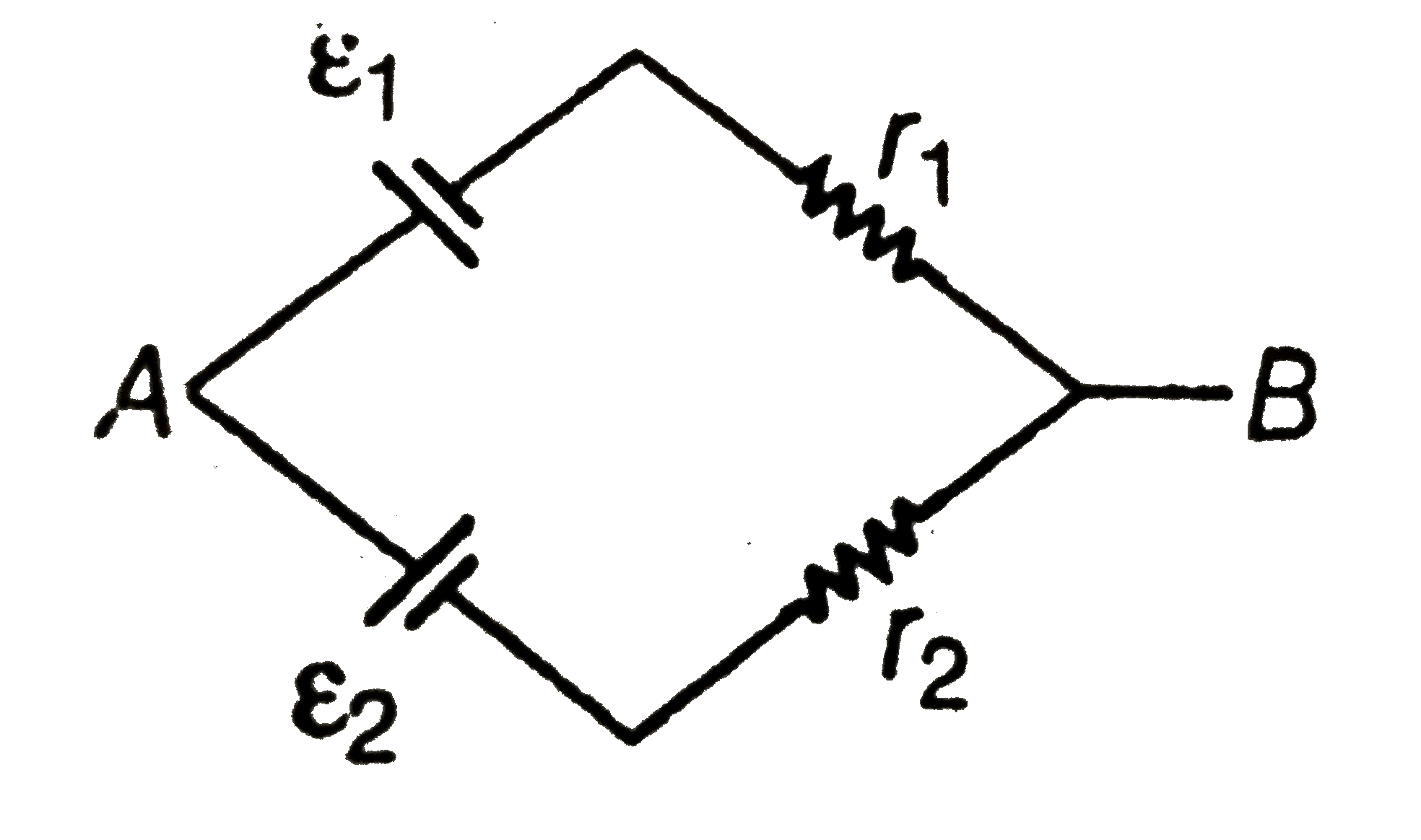
Two batteries of emf $ε_{1} and ε_{2} (ε_{2} > ε_{1})$ and internal resistance $r_{1} and r_{2}$ respectively are connected in parallel as shown in figure.
AThe equivalent emf $ε_{e q}$ of the two cells is between $ε_{1} and ε_{2}$ , i.e., $ε_{1} < ε_{e q} < ε_{2}$
Bthe equivalent emf $ε_{e q}$ is smaller than $ε_{1}$
CThe $ε_{e q}$ is given by $ε_{e q} = ε_{1} + ε_{2}$ always.
D $ε_{e q}$ is independent of internal resistance $r_{1} and r_{2}$ .
Question 3 - Select One
Two batteries of emf $ε_{1}$ and $ε_{2} (ε_{2} > ε_{1}$ and internal resistances $r_{1}$ and $r_{2}$ respectively are connected in parallel as shown in Fig. 2 (EP).1.

AThe equivalent emf $ε_{e q}$ of the two cells is between $ε_{1}$ and $ε_{2}, i . e ., ε_{1} < ε_{e q} < ε_{2}$
BThe quivalent emf $ε_{e q}$ is smaller than $ε_{1}$
CThe $ε_{e q}$ is given by $ε_{e q} = ε_{1} + ε_{2}$ always
D $ε_{e q}$ is independent of internal resistances $r_{1}$ and $r_{2}$

Two cells of emfs $ε_{1} and ε_{2}$ and internal resistances $r_{1} and r_{2}$ respectively are connected in parallel . Obtain expressions for the equivalent (i) resistance and , (ii) emf of the combination.

Topper's Solved these Questions

Similar Questions

Knowledge Check

Two batteris of emf $ε_{1}$ and $ε_{2}$ wit respective internal resistance $r_{1}$ and $r_{2}$ are connected in parallel. Now

Two batteries of emf $ε_{1} and ε_{2} (ε_{2} > ε_{1})$ and internal resistance $r_{1} and r_{2}$ respectively are connected in parallel as shown in figure.

Two batteries of emf $ε_{1}$ and $ε_{2} (ε_{2} > ε_{1}$ and internal resistances $r_{1}$ and $r_{2}$ respectively are connected in parallel as shown in Fig. 2 (EP).1.

MODERN PUBLICATION-CURRENT ELECTRICITY-REVISION EXERCISES (VERY SHORT ANSWER QUESTIONS)

Two cells of emfs ε1andε2 and internal resistances r1andr2 respectively are connected in parallel . Obtain expressions for the equivalent (i) resistance and , (ii) emf of the combination.

Topper's Solved these Questions

Similar Questions

Knowledge Check

Two batteris of emf ε1 and ε2 wit respective internal resistance r1 and r2 are connected in parallel. Now

Two batteries of emf ε1andε2(ε2>ε1) and internal resistance r1andr2 respectively are connected in parallel as shown in figure.

Two batteries of emf ε1 and ε2(ε2>ε1 and internal resistances r1 and r2 respectively are connected in parallel as shown in Fig. 2 (EP).1.

MODERN PUBLICATION-CURRENT ELECTRICITY-REVISION EXERCISES (VERY SHORT ANSWER QUESTIONS)

Two cells of emfs $ε_{1} and ε_{2}$ and internal resistances $r_{1} and r_{2}$ respectively are connected in parallel . Obtain expressions for the equivalent (i) resistance and , (ii) emf of the combination.

Two batteris of emf $ε_{1}$ and $ε_{2}$ wit respective internal resistance $r_{1}$ and $r_{2}$ are connected in parallel. Now

Two batteries of emf $ε_{1} and ε_{2} (ε_{2} > ε_{1})$ and internal resistance $r_{1} and r_{2}$ respectively are connected in parallel as shown in figure.

Two batteries of emf $ε_{1}$ and $ε_{2} (ε_{2} > ε_{1}$ and internal resistances $r_{1}$ and $r_{2}$ respectively are connected in parallel as shown in Fig. 2 (EP).1.