Two cells of same emf $ε$ , but different internal resistances $r_{1} and r_{2}$ are connected to an external resistance R, as shown. The voltmeter V reads zero. Find R in terms of $r_{1} and r_{2}$ , and the voltage across the cell of internal resistance $r_{2}$ .

Video Solution

|

Answer

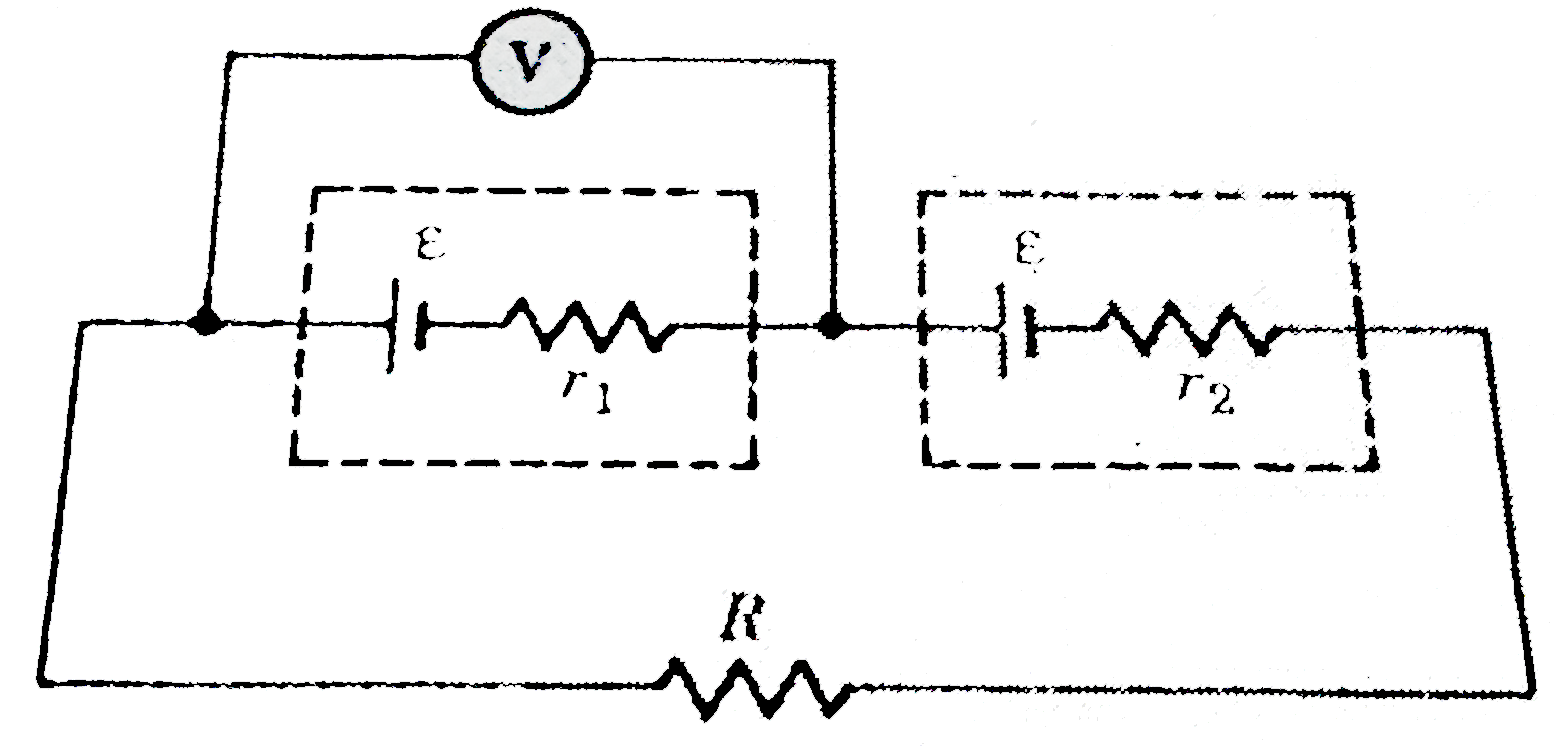
Step by step video & image solution for Two cells of same emf epsilon, but different internal resistances r_(1) " and " r_(2) are connected to an external resistance R, as shown. The voltmeter V reads zero. Find R in terms of r_(1) " and " r_(2), and the voltage across the cell of internal resistance r_(2). by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS CURRENT ELECTRICITY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Two cells of same emf $ε$ but of different internal resistances $r_{1}$ and $r_{2}$ are connected in series with an external resistance R. The potential drop across the first cell is found to be zero. The external resistance R is
A $r_{1} + r_{2}$
B $r_{1} - r_{2}$
C $r_{2} - r_{1}$
D $r_{1}^{2} / r_{2}$
Question 2 - Select One
Two cells of the same e.mf. e but different internal resistances $r_{1} and r_{2}$ are connected in series with an external resistance 'R'. The potential drop across the first cell is found to be zero. The external resistance Ris

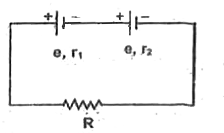A $r_{1} - r_{2}$
B $\frac{r_{1}}{r_{2}}$
C $r_{1} r_{2}$
D $r_{1} + r_{2}$
Question 3 - Select One
Tow cells with the same emf E and different internal resistances $r_{1}$ and $r_{2}$ are connected in series to an external resistances R . The value of R so that the potential difference across the first cell be zero is
A $\sqrt{r_{1} r_{2}}$
B $r_{1} + r_{2}$
C $r_{1} - r_{2}$
D $\frac{r_{1} + r_{2}}{2}$

SL ARORA-CURRENT ELECTRICITY-Problems From Competitive

Home
Ask Doubt
Profile