Two charged particles are placed at a distance 1.0 cm apart. What is the minimum possible magnitude of the electric force acting o each charge?
2.3×10−24N
6.2×10−34N
1.02×10−26N
4.2×10−27N
The correct Answer is:A
To find the minimum possible magnitude of the electric force acting on each charge when two charged particles are placed at a distance of 1.0 cm apart, we can follow these steps:
1. Understanding the Problem: We need to calculate the electric force between two charged particles that are 1.0 cm apart. The minimum possible magnitude of the electric force occurs when both charges are at their smallest possible value.
2. Identifying the Charge: According to the principle of quantization of charge, the smallest unit of charge is the elementary charge (e), which is approximately 1.6×10−19 coulombs. Therefore, we can assume both charges are equal to e.
3. Using Coulomb's Law: The electric force F between two point charges can be calculated using Coulomb's law, which is given by the formula:
F=kq1⋅q2r2
where:
- F is the electric force,
- k is Coulomb's constant (8.99×109N m2/C2),
- q1 and q2 are the magnitudes of the charges,
- r is the distance between the charges.
4. Substituting Values: In our case, both charges are q1=q2=e=1.6×10−19C and the distance r=1.0cm=0.01m. Thus, we can substitute these values into the formula:
F=k(1.6×10−19)⋅(1.6×10−19)(0.01)2
5. Calculating the Force:
- First, calculate (1.6×10−19)2:
(1.6×10−19)2=2.56×10−38
- Then, calculate (0.01)2:
(0.01)2=1.0×10−4
- Now, substitute these values into the force equation:
F=(8.99×109)2.56×10−381.0×10−4
- Simplifying this gives:
F=(8.99×109)⋅(2.56×10−34)=2.30×10−24N
6. Final Result: The minimum possible magnitude of the electric force acting on each charge is approximately:
F≈2.30×10−24N
F=kq1⋅q2r2
where:
- F is the electric force,
- k is Coulomb's constant (8.99×109N m2/C2),
- q1 and q2 are the magnitudes of the charges,
- r is the distance between the charges.
F=k(1.6×10−19)⋅(1.6×10−19)(0.01)2
- First, calculate (1.6×10−19)2:
(1.6×10−19)2=2.56×10−38
- Then, calculate (0.01)2:
(0.01)2=1.0×10−4
- Now, substitute these values into the force equation:
F=(8.99×109)2.56×10−381.0×10−4
- Simplifying this gives:
F=(8.99×109)⋅(2.56×10−34)=2.30×10−24N
F≈2.30×10−24N
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced44videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Comprehension36videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Medical entrances s gallery21videos
ELASTICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective15videos
EXPERIMENTS
Similar Questions
Two point charges +4q and +q are placed 30cm apart. At what point on the line joining them is the electric field zero
View SolutionTwo equal charges are placed at a separtion of 1.0 m. What should be the magnitude of the charges so that the force between them equals of a 50 kg person?
View SolutionFig. shows some of the electric field lines due to three point charges arranged along the vertical axis. All three charges have the same magnitude.
(a) What are the signs of each of the three charges? Explain your reasoning.
(b) At what points(s) is the magnitude of the electric field the smallest? Explain your reasoning. Explain how the fields produced by each individual point charge combine to give a small net field at this point or points.
(c ) Two point charges q and -q are placed at a distance d apart. What are the points at which the resultant electric field is parallel to the line joining the two charge?
 .View Solution
.View SolutionTwo small iron particles, each of mass 280 mg, are. placed at a distance 10 cm apart. If 0.01% of the electron. of one particle are transferred to the other, find the. electric force between them. Atomic weifht of iron is 56gmol− and there are 26 electrons in each atom of iron.
View SolutionThree point charges q are placed at three vertices of an equilateral triangle of side a. Find magnitude of electric force on any charge due to the other two.
View SolutionThe magnitude of electric intensity at a distance x from a charge q is E.An identical charge is placed at a distance 2x from it Then the magnitude of the force it experience is ..
View SolutionTen positively charged particles are kept fixed on the x-axis at points x=10cm, 20cm, 30cm, …, 100cm. The first particle has a charge 1.0×10−8C, the second 8×10−8 C, the third 27×10(−8)C and so on. The tenth particle has a charge 1000×10−8C. find the magnitude of the electric force acting on a 1 C charge placed at the origin.
View SolutionTwo point charges 2q and 8q are placed at a distance r apart. Where should a third charge −q be placed between them so that the electrical potential energy of the system is a minimum
View SolutionTwo point charges +4q and +q are placed at a distance L apart. A third charge Q is so placed that all the three charges are in equilibrium. Then location. And magnitude of the third charge will be
View SolutionTwo point charges +10−7C and −10−7C are placed at A and B 20 cm apart as shown in the figure. Calculate the electric field at C, 20 cm apart from both A and B.
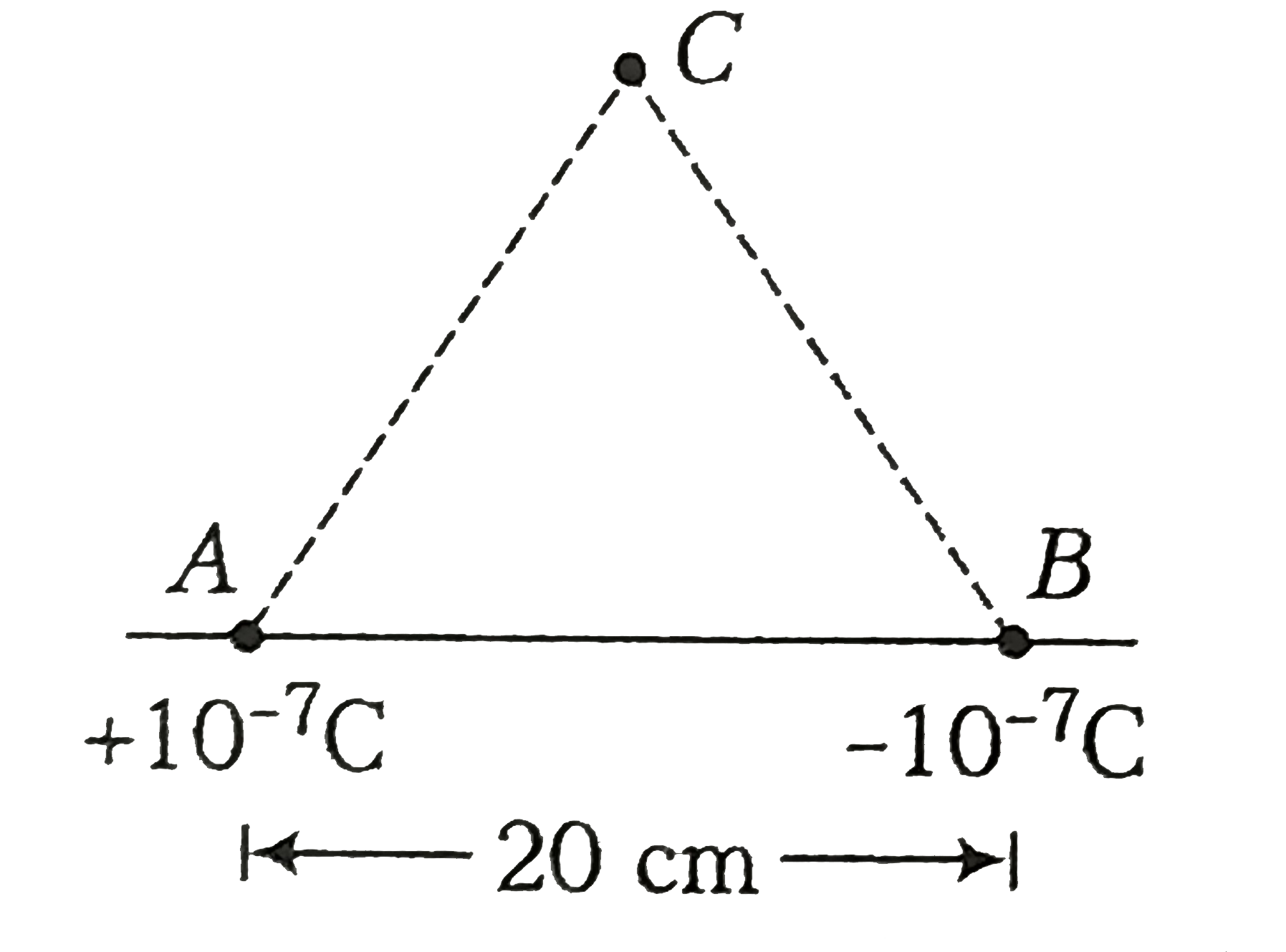 View Solution
View Solution

