Two charges 4×10−6Cand−2×10−6C are placed 45 cm, apart. Find out the location of a point, lying on the line joining two charges, where the electric potential is zero. Solution in Punjabi
q1=4×10−6C
q2=2×10−6C
Distance between q1andq2=r45cm
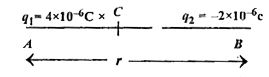
Let C is a point at distance x from q1 whose electric potential is zero and BC -r-x=(45 - x) cm.
Potential at C due to q1=V1=(1)14πε0q1x
Potential at C due to q2=V2
=14πε(0))q2r−x
∴ Potential at point C should be zero
∴V1+V2=0
⇒V1=−V2
14πε0=11/(4πε0)q2(r−x)
9×109×4×10−6x
=−9×109×(−2×10−6)(45−x)
⇒4x=245−x
⇒2x=180−4x
⇒6x=180
x=30 cm from q1
So potential will zro at ditance at 30 cm from chage 4×10−6C.
Topper's Solved these Questions
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIALEXERCISE - MOST EXPECTED QUESTIONS7videos
ELECTROSTATIC POTENTIAL
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIALEXERCISE - MOST EXPECTED QUESTIONS (2 Marks Questions)4videos
ELECTROSTATIC POTENTIAL
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIALEXERCISE - LONG ANSWERTYPE QUESTIONS (5/6 Marks Questions)8videos
ELECTROSTATIC POTENTIAL
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - ELECTRONIC DEVICES SOLIDSEXERCISE - Most Expected Questions9videos
ELECTRONIC DEVICES SOLIDS
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - FORCE ON A CHARGE EXERCISE - NUMERICAL PROBLEMS14videos
FORCE ON A CHARGE
Similar Questions
Name the physical quantity whose SI unit is volt metre−1.
05:19View SolutionDraw an equipotential surface for a system consisting of two charges Q, -Q separated by a distance r in air.
02:02View SolutionDefine electric potential. What is the SI unit of potential? Obtain an expression for electric potential at a distance r from isolated unit positive charge.
04:33View SolutionWhy semiconductors are doped?
06:15View SolutionAn electron (with charge 1.6×10−19C) moving at right angles to a uniform magnetic field completes a circular orbit in 10−6sec. Calculate the vlaue of magnetic field. Given mass of electron =9×10−31kg.
03:44View SolutionTwo charges 3×10−8Cand−2×10−8C are located 15 cm apart. At what point on the line joining the two charges is the electric potential zero ? Take the potential at infinity to be zero.
08:12View SolutionTwo positive charges of magnitude 4 C and 6 C are placed 10 cm apart . The electric potential at a distance of 10 cm from the middle point on the right bisector of the line,joining the two charges is
07:10View SolutionTwo particles A and B having charges of 4xx10^(-6)C and -8xx10^(-6) C respectively, are held fixed at a separation of 60 cm. Locate the point (s) on the line AB where the electric potential is zero.
05:09View SolutionTwo charges 3xx10^(-8)C and -2xx10^(-8)C are located 15 cm apart. At what point on the line joining the two to be charges is the electric potential zero ? Take the potential at infinity to be zero.
01:48View SolutionTwo electric charges 12 mu C and -6 mu C are placed 20 cm apart in air, there will be a point P at which electric potential is zero on the line joining these two charges and out side excluding the region between them. The distance of P from -6 mu C charge is
03:56View Solution4.3×10−6C तथा −2×10−8C के दो आवेश परस्पर 15cm दूर है। इन दोनों आवेशों को मिलाने वाली रेखा के किस बिन्दु पर विद्युत विभव शून्य होगा? अनन्त पर विद्युत विभव शून्य मान लो।
05:42View SolutionTwo point charge - 5 mu C and + 3 mu C are placed 64 cm apart. At what points on the line joining the two charges is the electric potential zero. Assume the potential at infinity to be zero.
04:24View SolutionTwo charges 3×10−8Cand−2×10−8C are located 15 cm apart. At what point on the line joining the two charges is the electric potential zero ? Take the potential at infinity to be zero.
04:34View SolutionTwo charges 5×10−8Cand−3×10−8C are located 16 cm apart. At what points on the line joining the two charges is the electric potential zero ? Take the potential at infinity to be zero.
04:34View SolutionTwo charge 5×10−8C and −3×10−8 C are located 16 cm apart. At what point(s) on the line joining the two charges is the electric potential zero ? Take the potential at infinity to be zero.
02:16View Solution

