Two charges A and B of −5μC each are placed at a separation of 20 cm . Another charge C of +3 μC is placed at a separation of 20 cm from both the charges A and B . What should be the nature and magnitude of the charge to be placed at the midpoint between A and B so that net force on charge C is zero ?
To solve the problem step-by-step, we need to analyze the forces acting on charge C due to charges A and B, and then determine the charge that must be placed at the midpoint between A and B to ensure that the net force on charge C is zero.
Step 1: Identify the charges and their positions
- Charge A = -5 µC (located at point A)
- Charge B = -5 µC (located at point B, 20 cm from A)
- Charge C = +3 µC (located at point C, 20 cm from both A and B)
- Midpoint M between A and B is where we will place charge Q2.
Step 2: Determine the forces acting on charge C
- The force F1 on charge C due to charge A (attraction because A is negative):
F1=k|QA⋅QC|r2=k|−5×10−6⋅3×10−6|(0.2)2
- The force F2 on charge C due to charge B (also attraction):
F2=k|QB⋅QC|r2=k|−5×10−6⋅3×10−6|(0.2)2
Step 3: Calculate the forces
Since both forces F1 and F2 are equal in magnitude and directed towards charges A and B respectively, we can denote:
F1=F2=F
Where:
F=k15×10−120.04=15k0.04=375k(in Newtons)
Step 4: Introduce charge Q2 at midpoint M
- Charge Q2 will exert a repulsive force F3 on charge C because both are positive:
F3=k|Q2⋅QC|d2
Where d is the distance from M to C, which is √(0.1)2+(0.1√3)2=0.2√32=0.1√3.
Step 5: Set the net force on charge C to zero
For the net force on charge C to be zero:
F1+F2=F3
Since F1=F2=F:
2F=F3
Substituting for F3:
2F=k|Q2⋅3×10−6|(0.1√3)2
This simplifies to:
2⋅375k=k|Q2⋅3×10−6|0.03
Cancelling k from both sides:
750=|Q2⋅3×10−6|0.03
Solving for Q2:
Q2=750⋅0.033×10−6=22.53×10−6=7.5×10−3=7.5mC
Step 6: Determine the nature of charge Q2
Since charge C is positive, and we need a repulsive force to counteract the attractive forces from A and B, charge Q2 must also be positive.
Final Answer
The charge to be placed at the midpoint between A and B should be:
- Nature: Positive
- Magnitude: 7.5mC
- Charge A = -5 µC (located at point A)
- Charge B = -5 µC (located at point B, 20 cm from A)
- Charge C = +3 µC (located at point C, 20 cm from both A and B)
- Midpoint M between A and B is where we will place charge Q2.
- The force F1 on charge C due to charge A (attraction because A is negative):
F1=k|QA⋅QC|r2=k|−5×10−6⋅3×10−6|(0.2)2
- The force F2 on charge C due to charge B (also attraction):
F2=k|QB⋅QC|r2=k|−5×10−6⋅3×10−6|(0.2)2
Since both forces F1 and F2 are equal in magnitude and directed towards charges A and B respectively, we can denote:
F1=F2=F
Where:
F=k15×10−120.04=15k0.04=375k(in Newtons)
- Charge Q2 will exert a repulsive force F3 on charge C because both are positive:
F3=k|Q2⋅QC|d2
Where d is the distance from M to C, which is √(0.1)2+(0.1√3)2=0.2√32=0.1√3.
For the net force on charge C to be zero:
F1+F2=F3
Since F1=F2=F:
2F=F3
Substituting for F3:
2F=k|Q2⋅3×10−6|(0.1√3)2
This simplifies to:
2⋅375k=k|Q2⋅3×10−6|0.03
Cancelling k from both sides:
750=|Q2⋅3×10−6|0.03
Solving for Q2:
Q2=750⋅0.033×10−6=22.53×10−6=7.5×10−3=7.5mC
Since charge C is positive, and we need a repulsive force to counteract the attractive forces from A and B, charge Q2 must also be positive.
The charge to be placed at the midpoint between A and B should be:
- Nature: Positive
- Magnitude: 7.5mC
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Practice Problems
88 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Conceptual Questions
51 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
14 Videos
Similar Questions
Two chargea 2.0×10−6C are placed at a separation of 10 cm. where should a third charge be placed such that it experiences no net force due to these charges.
View SolutionTwo charges +10μC and +20μC are placed at a. separation of 2 cm. Find the electric potential due to the. pair at the middle point of the line joining the two charges.
View Solution
Knowledge Check
A point charge of +6μC is placed at a distance 20 cm directly above the centre of a square of side 40 cm . The magnitude of the flux through the square is
Aε0B1ε0Cε0×10−6D1ε0×10−6A charge 10 esu is placed at a distance of 2 cm from a charge 40 esu and 4 cm from another charge -20 esu. The potential energy of the charge 10 esu is : (in ergs)
A87.5B112.5C150Dzero
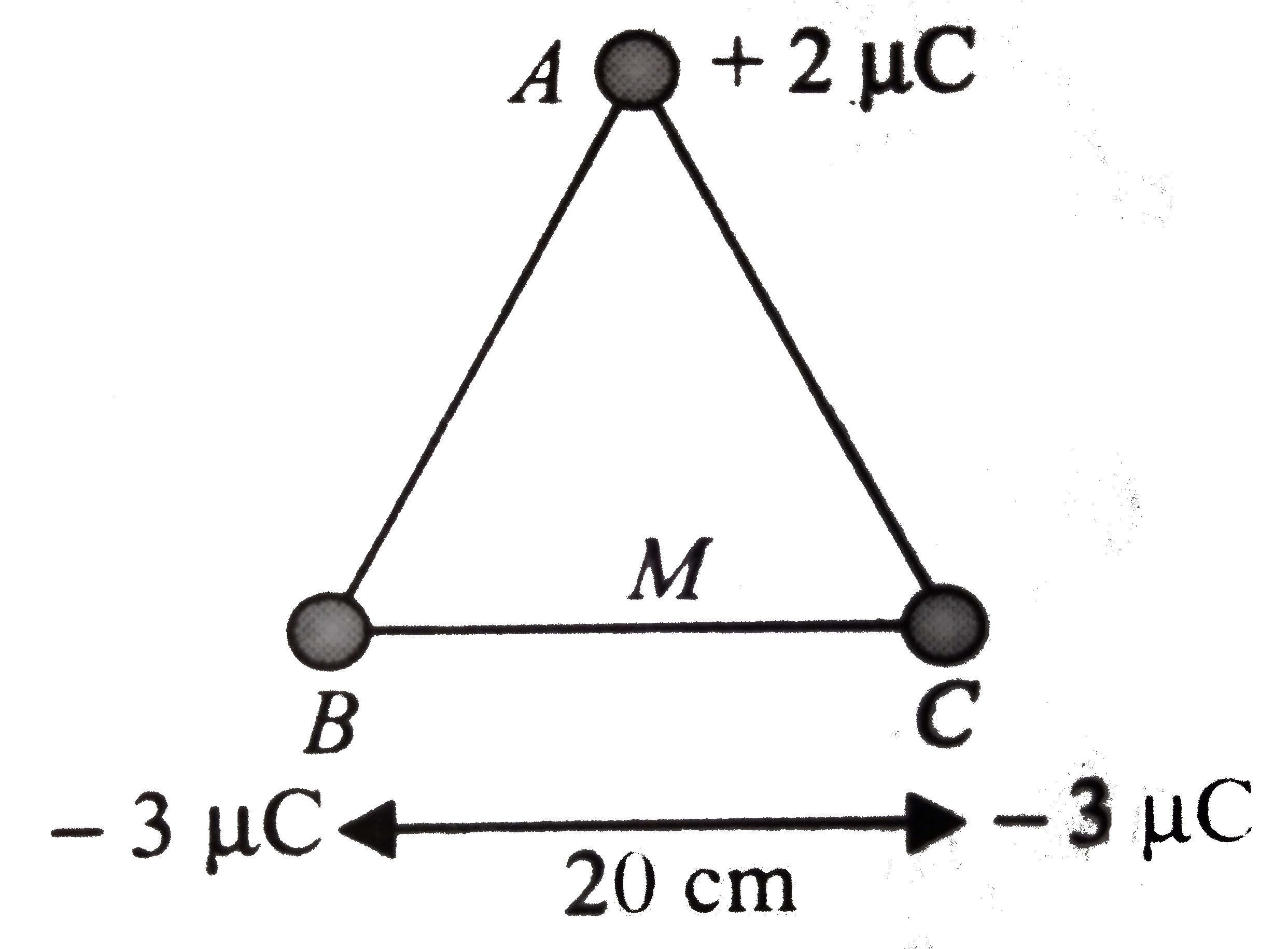
Three point charges of +2μC,−3μCand−3μC are kept at the vertices A,B and C , respectively of an equilateral triangle of side 20 cm as shown in What should be the sign and magnitude of the charge to be placed at the mid-point (M) of side BC so that the charge at A remains in equilibrium?
(##U_LIK_SP_PHY_XII_C01_E09_017_Q01.png" width="80%">
View SolutionTwo equal charges are placed at a separtion of 1.0 m. What should be the magnitude of the charges so that the force between them equals of a 50 kg person?
View SolutionThree point charges of +2μC,−3μC , and −3μC are kept at the vertices A, B, and C, respectively of an equilatreral triangle of side 20 cm. what should be the sign and magnitude of the charge (q) to be placed at the midpoint (M) of side BC so that the charge at A remains in equilibrium?
View SolutionTwo charges +0.4μC and−0.2μC are placed on adjacent vertices of a square of side 10 cm. Another charge of 1.2μC is placed at the centre af the square Calculate the force and its direction in the charge kept in the centre .
View SolutionTwo equal charges, 2.0×10−7C each, are held fixed at a separation of 20cm. A third charge of equal magnitude is placed midway between the two both the charges. How much work is done by the electric field during the process?
View SolutionA charge +2 μC is placed at a point A (2,1,0). Another charge −3μC is placed at a point B (4,2,-1). Calculate net force on a charge +5μC placed at a point C (-1,3,2).
View Solution
