Two charges –q and +q are located at points (0, 0, –a) and (0, 0, a), respectively.
(a) What is the electrostatic potential at the points (0, 0, z) and (x, y, 0) ?
(b) Obtain the dependence of potential on the distance r of a point from the origin when .
(c) How much work is done in moving a small test charge from the
point (5,0,0) to (–7,0,0) along the x-axis? Does the answer change if the path of the test charge between the same points is not along the x-axis?Solution in Gujrati
(a) When point P is near to charge + q,
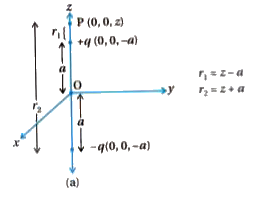
Electrostatic potential at point P
2aq=P)
When point P is near to charge -q
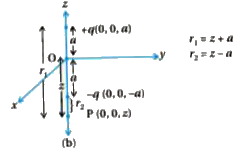
Similarly ,
Potential at point P
If any point (x, y, 0) is in xy-plane and hence it is at same distance from - q to + q on perpendicular bisector of z-axis then potential at such point is,
(b) If point P is at distance of r from origin 0, then Putting z = r in equation (1) and (2),
If then is neglected compare with
(c) Points (5, 0, 0) and (-7, 0, 0) are on x-axis so they are on the perpendicular bisector of dipole (equatorial line) hence they are at the same distance from both the charges. As a result potential is zero.
Now if work done in moving a test charge
from (5,0,0) to (-7,0,0) ,
W =
W =0
No, because electric field is conservation field, the work done in moving a test charge between two point is independent of the path
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - KUMAR PRAKASHANCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Section B ( Numerical From DARPAN. Based on Textbook )
19 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - KUMAR PRAKASHANCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Section B (questions)
2 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - KUMAR PRAKASHANCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Section B Numericals
16 Videos
- ELECTROMAGNETIC WAVESBOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - BOARD.S QUESTION PAPER MARCH - 2020 (PART - B) SECTION - C
5 Videos
- MAGNETISM AND MATTERBOOK - KUMAR PRAKASHANCHAPTER - MAGNETISM AND MATTEREXERCISE - SECTION D Multiple Choice Questions (MCQs) (MCQs asked in Competitive Exams) MCQs asked in Board Exam and GUJCET
7 Videos
Similar Questions
An electric field is represented by →E=Axˆi where A = 10Vm2 . Find the potential of the origin with respect to the point (10,20) m.
View SolutionA slab of material of dielectric constant K has the same area as the plates of a parallel plate capacitor but has a thickless (12)d. Where d is the separation of the plates . How is the capacitance changed when the slab is inserted between the plates
View SolutionCalculate the potential at a point P due to a charge of 4×10−7 C located 9 cm away.
View SolutionDetermine the current in each branch of the given network.

View SolutionAt a place on earth the vertical component of earth's magnetic field is √3 times its horizontal component. The angle of dip at this place is …...
View SolutionTwo charges -q and +q are located at points (0,0,-a) and (0,0,a) respectively. (i) What is the electrostatic potential at the points at the points (0,0,z) and (x,y,0)? (ii) Obtain the depentence of potential on the distance r of the point form the origin, when (r)/(a) gt gt 1 . (iii) How much work is done in moving a small test charge from the point (5,0,0) to (-7,0,0) along the x-axis. Does the answer charge if path of test charge between the same points is not along the x-axis ?
View SolutionTwo charges -q and +q are located at points (0, 0, –a) and (0, 0, a), respectively.
(a) What is the electrostatic potential at the points (0, 0, z) and (x, y, 0) ? (b) Obtain the dependence of potential on the distance r of a point from the origin when r/a>>1.
(c) How much work is done in moving a small test charge from the point (5,0,0) to (–7,0,0) along the x-axis? Does the answer change if the path of the test charge between the same points is not along the x-axis?
View Solutionबिंदु (0, 0 -a) तथा (0, 0, a) पर दो आवेश क्रमश : -q और +q स्थित हैं ।
(a) बिंदुओं (0, 0, z) और (x, y, 0) पर स्थिरविद्युत विभव क्या है ?
(b) मूल बिंदु से किसी बिंदु कि दुरी n पर विभव कि निर्भरता ज्ञात कीजिए, जबकि r/a>>1 है।
(c) x -अक्ष पर बिंदु (5, 0, 0) से बिंदु (-7, 0, 0) तक परीक्षण आवेश को ले जाने में किया कार्य करना होगा? यदि परिक्षण आवेश के उन्हीं बिंदुओं के बीच x -अक्ष से होकर न ले जाएँ तो क्या उत्तर बदल जाएगा?
View SolutionTwo charges -q and +q are located at points (0,0-a) and (0,0-a), respectively. (a) What is the electrostatic potential at the points (0,0,z) and (x,y,0) ? (b) Obtain the dependence of potential on the distance r of a point from the origin when r//a gt gt1. (c) How much work is done in moving a small test charge from the point (5,0,0) to (-7,0,0) along the x-axis? Does the answer change if the path of the test charge between the same points is not along the x-axis ?
View Solutionबिंदु (0, 0, -a) तथा (0, 0, a) पर दो आवेश क्रमशः -q और +q स्थित हैं।
बिंदुओं (0, 0, z) और (x, y, 0) पर स्थिरवैद्युत विभव क्या है
View Solutionबिन्दु (0, 0, - a) तथा (0, 0, a) पर दो आवेश क्रमश:-q और +q स्थित हैं।
मूलबिन्दु से किसी बिन्दु की दूरी r पर विभव की निर्भरता (dependency) ज्ञात कीजिए, जबकि ra>>1 है।
View SolutionTwo charges -q and + q are located at points A (0, 0, -a ) and B(0, 0 + a ) . How much work is done in moving a test charge from point (b, 0, 0 ) to Q (-b, 0, 0) ?
View SolutionTwo charges -q and +q are located at points (0,0,-a) and (0,0,a) respectively. a. What is the electrostatic potential at the points (0,0,z) and (x,y,0)? b. Obtain the dependence of potential on the distance r of a point from the origin which r/a gt gt 1 . c. How much work is done in making a small test charge from the point (5,0,0), (-7,0,0) along the x-axis? Does the answer change if the path of hte test charge between the same points is not along the x-axis?
View SolutionTwo charges –q and +q are located at points (0, 0, –a) and (0, 0, a), respectively.
(a) What is the electrostatic potential at the points (0, 0, z) and (x, y, 0) ?
(b) Obtain the dependence of potential on the distance r of a point from the origin when r/a>>1 .
(c) How much work is done in moving a small test charge from the point (5,0,0) to (–7,0,0) along the x-axis? Does the answer change if the path of the test charge between the same points is not along the x-axis?
View SolutionTwo charges –q and +q are located at points (0, 0, –a) and (0, 0, a), respectively.
(a) What is the electrostatic potential at the points (0, 0, z) and (x, y, 0) ?
(b) Obtain the dependence of potential on the distance r of a point from the origin when r/a>>1 .
(c) How much work is done in moving a small test charge from the point (5,0,0) to (–7,0,0) along the x-axis? Does the answer change if the path of the test charge between the same points is not along the x-axis?
View Solution
