Two coaxial solenoids of different radii carry current I in the same direction . Let →F1 be the magnetic force on yhr inner solenoid due to the outer one and →F2 be the magnetic force ont he outer solenoid due to the inner one . Then :
→F1=→F2=0
→F1 is radially inwards and →F2 is radially outwards
→F1 is radially inwards and →F2=0
→F1 is radially outwards and →F2=0
The correct Answer is:A
→F1=→F2=→0 (∴BIlsinθ In this case θ=0∘ )
Topper's Solved these Questions
- 15 MAGNETIC EFFECTS OF CURRENTSBOOK - MODERN PUBLICATIONCHAPTER - 15 MAGNETIC EFFECTS OF CURRENTSEXERCISE - Recent Competitive Questions
31 Videos
- 15 MAGNETIC EFFECTS OF CURRENTSBOOK - MODERN PUBLICATIONCHAPTER - 15 MAGNETIC EFFECTS OF CURRENTSEXERCISE - Multiple choice questions (Level - II) Paragraph questions
42 Videos
- ATOMS, MOLECULES AND NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - ATOMS, MOLECULES AND NUCLEIEXERCISE - Recent Competitive Questions
40 Videos
Similar Questions
Two coaxial solenoids of different radius carry current I in the same direction. −→F1 be the magnetic force on the inner solenoid due to the outer one and −→F2 be the magnetic force on the outer solenide due to the inner one. Then
View SolutionTwo long coaxial insulated solenoids, S1andS2 of equal lengths are wound one over the other as shown in the figure. A steady current "I" flow through the inner solenoid S1 to the other end B, which is connected to the outer solenoid S2 through which the same current "I" flows inthe opposite direction so as to come out at end A. If n1 and n2 are the number of turns per unit length, find the magnitude and direction of the net magnetic field at a point (i) inside on the axis and (ii) outside the combined system.
View Solution
Knowledge Check
Two coaxial solenoids of different radius carry current I in the same direction. −→F1 be the magnetic force on the inner solenoid due to the outer one and −→F2 be the magnetic force on the outer solenide due to the inner one. Then
A−→F1 is radially inward and −→F2B−→F1 is radially outwards and −→F2=0C−→F1=−→F2=0D−→F1 is radially inwards and −→F2 is radially outwardsTwo concentric coils carry the same current in opposite directions. The diameter of the inner coil is equal currents. The outer coil. If the magnetic field produced by the outer coil at the common centre are 1T, the net field at the centre is
A1TB2TC3TD4T
Two long coaxical insulated solenoid's S1 and S2 of equal lengths are would one over the other as shown in figure. A steady current 'T' flows through the inner solenoid S1 to the other end B, which is connected to the outer solenoid S2 through which the same current flows in opposite direction so as to come out at end A. If n1 and n2 are the number of turns per unit length, find the magnitude and direction of net magnetic field at a point (i) inside on the axis and (ii) outside the combined system.
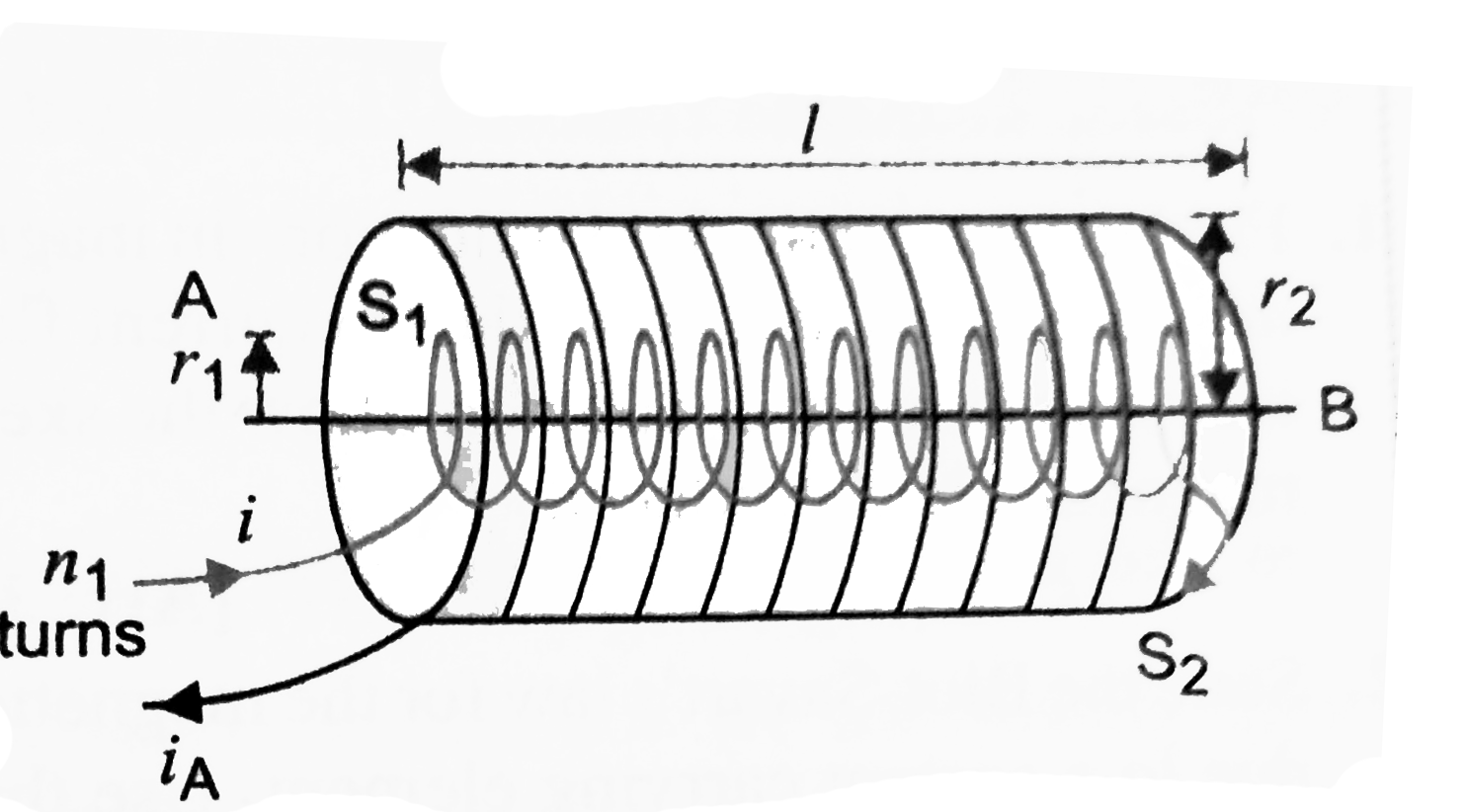
View SolutionTwo long coaxical insulated solenoid's S1 and S2 of equal lengths are would one over the other as shown in figure. A steady current 'T' flows through the inner solenoid S1 to the other end B, which is connected to the outer solenoid S2 through which the same current flows in opposite direction so as to come out at end A. If n1 and n2 are the number of turns per unit length, find the magnitude and direction of net magnetic field at a point (i) inside on the axis and (ii) outside the combined system.

View SolutionTwo long co-axial solenoids have radii, and number of turns per unit length equal to r1,r2 and n1,n2 respectively where suffix 1 refers to the outer solenoid and 2 refers to the inner solenoid. Length of both is l. The current in the outer solenoid is made to grow as I1=kt where t is time. Resistance of the wire used in inner solenoid is R. Write the current induced in the inner solenoid assuming that it is shorted.

View SolutionDeduce an expression for the mutual inductance of two long coaxial solenoids but having different radii and different number of turns.
Or
Obtain the expression for the mutual inductance of two long coaxial solenoids S1 and S2 wound one over the other, each of length I and radii r1andr2, and number of turns per unit length n1andn2 respeetively, when a current I is set up in the outer solenoid S2.
View Solution(a) State Ampère's circuital law expressing it in the integral form.
(b) Two long coaxial insulated solenoids S1 and S2 of equal lengths are wound one over the other as shown in the figure. A steady current 'I' flows through the inner solenoid S1 , to the other end B which is connected to the outer solenoid S2 , through which the same current 'I' flows in the opposite direction so as to come out at end A. If n1 , and n2 are the number of turns per unit length, find the magnitude and direction of the net magnetic field at a point (i) inside on the axis and (ii) outside the combined system.
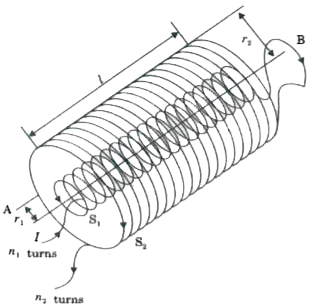
View SolutionTwo toroidal solenoids are wound around the same pipe so that the magnetic field of one passes through the turns of the other. Solenoid 1 has 700 turns and solenoid 2 has 400 turns. When the current in solenoid 1 is 6.52A, the average flux through each turn of solenoid 2 is 0.0320Wb.
(a) What is the mutual inductance of the pair of solenoids?
(b) When the current in solenoid 2 is 2.54A, what is the average flux through each solenoid 1?
View Solution
