Two concentric shells have masses $M$ and $m$ and their radii are $R$ and $r$ , respectively, where $R > r$ . What is the gravitational potential at their common centre?

$- \frac{G M}{R}$

$- \frac{G M}{r}$

$- G [\frac{M}{R} - \frac{m}{r}]$

$- G [\frac{M}{R} + \frac{m}{r}]$

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:D

Two concentric spherical shells $A$ and $B$ of radii $R$ and $2 R$ and mases $4 M$ , and $M$ , respectively are placed in space as shown in Fig. The gravitational potential at $P$ at a distance $r (R < r < 2 R)$ from the centre of shells is

A $- \frac{4 G M}{R}$
B $- \frac{9 G M}{2 R}$
C $- \frac{4 G M}{3 R}$
Dnone of these
Two concentric spheres kept in air have radii R and r. They have similar charge and equal surface charge density $σ$ . The electrical potential at their common centre is (where, $ε_{0} =$ permittivity of free space)
A $\frac{σ (R + r)}{ε_{0}}$
B $\frac{σ (R - r)}{ε_{0}}$
C $\frac{σ (R + r)}{2 ε_{0}}$
D $\frac{σ (R + r)}{4 ε_{0}}$
Assertion : Two spherical shells have masses $m_{1} and m_{2}$ . Their radii are $r_{1} and r_{2}$ . Let $r$ be the distance of a point from centre. Then gravitational field strength and gravitational potential both are equal to zero for $O < r < r_{1}$

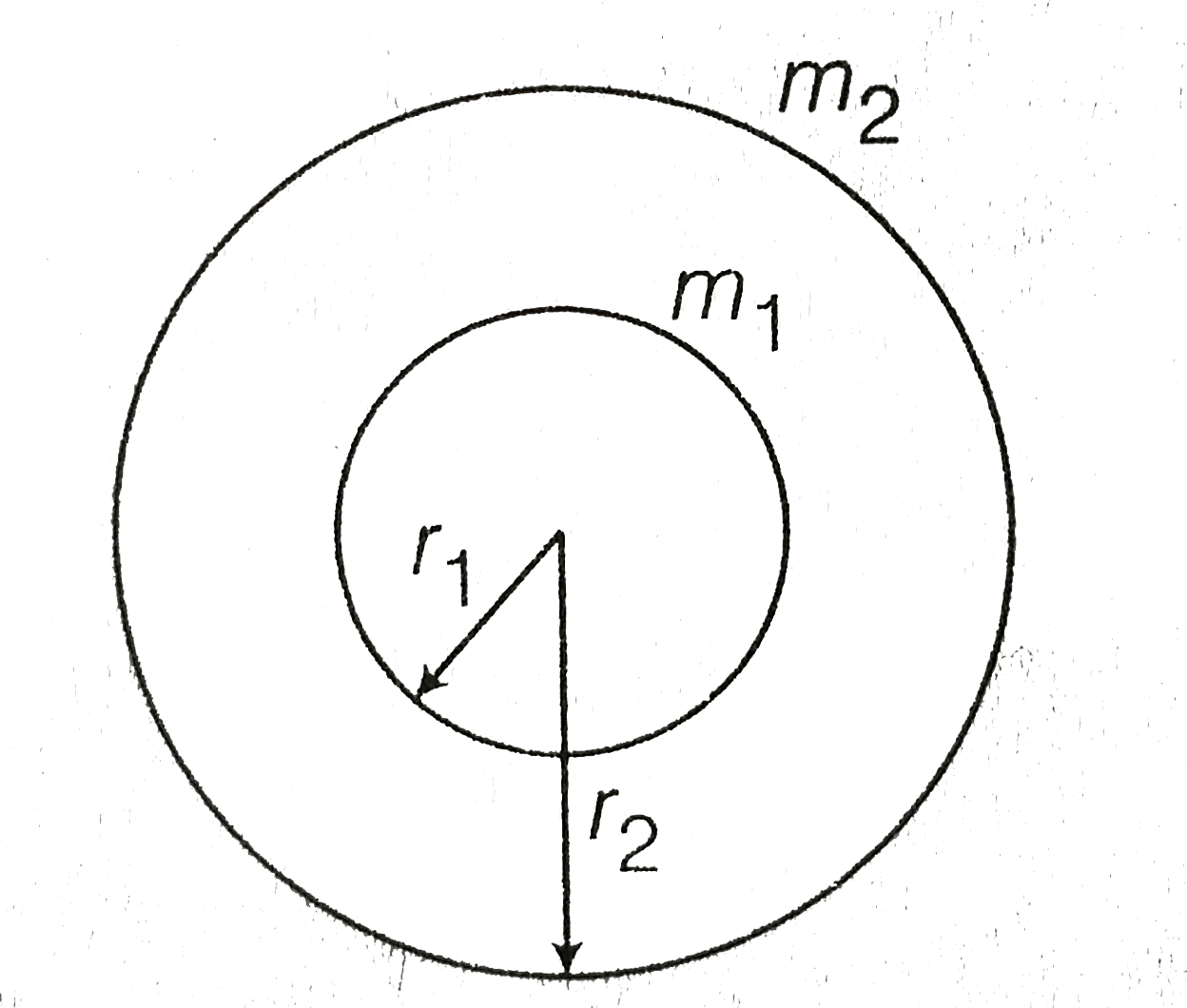
Reason : In the region $r_{1} < r < r_{2}$ , gravitational field strength due to $m_{2}$ is zero. But gravitational potential due to $m_{2}$ is constant (but non-zero).
AIf both Assertin and Reason are correct and Reason is the correct explanation of Assertion
BIf both Assertion and Reason are correct but Reason is not the correct explanation of Assertion
CIf Assertion is true but Reason is false
DIf Assertion is false but Reason is true