Two discs of moment of inertia I1 and I2 are rotating separately with angular velocities ω1 and ω2 respectively about perpendicular axis passing through their centres. If these two rotating discs are connected coaxially then the rotational kinetic energy of the composite system will be
I1ω1+I2ω22(I1+I2)
(I1+I2)(ω1+ω2)2
(I1ω1+I2ω2)22(I1+I2)
(I1+I2)(ω1+ω2)22
The correct Answer is:C
Topper's Solved these Questions
- ROTATION OF RIGID BODIES BOOK - CHHAYA PUBLICATIONCHAPTER - ROTATION OF RIGID BODIES EXERCISE - Very Short Answer Type Questions
5 Videos
- ROTATION OF RIGID BODIES BOOK - CHHAYA PUBLICATIONCHAPTER - ROTATION OF RIGID BODIES EXERCISE - Very Short Answer Type Questions ( Based on Torque )
2 Videos
- ROTATION OF RIGID BODIES BOOK - CHHAYA PUBLICATIONCHAPTER - ROTATION OF RIGID BODIES EXERCISE - EXERCISE ( Based on Rotational Kinetic Energy )
5 Videos
- QUESTION PAPERS OF WBCHSE -2018BOOK - CHHAYA PUBLICATIONCHAPTER - QUESTION PAPERS OF WBCHSE -2018EXERCISE - SECTION -II
20 Videos
- SIMPLE HARMONIC MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - CBSE SCANNER
16 Videos
Similar Questions
Two discs A and B are in contact and rotating with angular velocity with angular velocities ω1andω2 respectively as shown. If there is no slipping between the discs, then
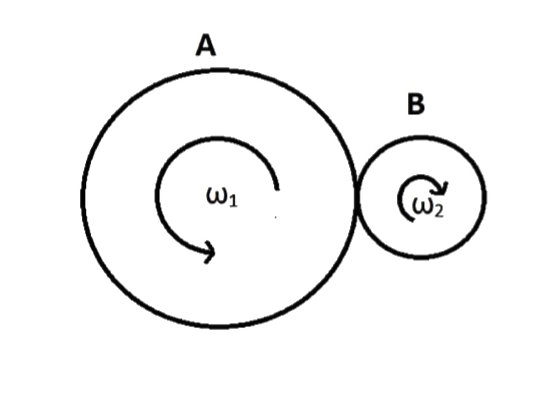
View SolutionTwo discs A and B are in contact and rotating with angular velocity with angular velocities ω1andω2 respectively as shown. If there is no slipping between the discs, then

View Solution
Knowledge Check
Two discs of moment of inertia I1 and I2 and angular speeds ω1 and ω2 are rotating along the collinear axes passing through their center of mass and perpendicular to their plane. If the two are made to rotate combindly along the same axis the rotational K.E. of system will be
AI1ω1+I2ω22(I1+I2)B(I1+I2)(ω1+ω2)22C(I1ω1+I2ω2)22(I1+I2)DNone of theseTwo uniform circular rough disc of moment of inertia I1 and I12 are rotating with angular velocity ω1 and ω12 respectively in same direction. Now one disc is placed the other disc co-axially. The change in kinetic energy of the system is :
A−124I1ω12B124I1ω12C112I1ω12D−112I1ω12Two discs of moments of inertia l1 and l2 and angular speeds ω1 and ω2 are rotating along collinear axes pass through their centre of mass and perpendicular to their plane. If the two are made to rotate jointly along the same axis, the rotational K.E. of system will be
A(l1ω1+l2ω2)22(l1+l2)B(l1+l2)(ω1+ω2)2C(l1+l2)(ω1+ω2)2DNone of these
Two discs of moment of inertia I1 and I2 and angular speeds ω1 and ω2 are rotating along the collinear axes passing through their center of mass and perpendicular to their plane. If the two are made to rotate combindly along the same axis the rotational K.E. of system will be
View SolutionTwo uniform circular rough disc of moment of inertia I1 and I12 are rotating with angular velocity ω1 and ω12 respectively in same direction. Now one disc is placed the other disc co-axially. The change in kinetic energy of the system is :
View SolutionTwo discs of moments of inertia I1 and I2 about their respective axes, rotating with angular frequencies, ω1 and ω2 respectively, are brought into contact face to face with their axes of rotation coincident. The angular frequency of the composite disc will be A.
View SolutionTwo discs of moments of inertia I1 and I2 about their respective axes , rotating with angular frequencies ω1 and ω2 respectively, are brought into contact face to face with their axes of rotation coincident. The angular frequency of the composite disc will be
View SolutionTwo discs of moments of inertia I1 and I2 about their respective axes , rotating with angular frequencies ω1 and ω2 respectively, are brought into contact face to face with their axes of rotation coincident. The angular frequency of the composite disc will be
View Solution
