Two forces of magnitudes 3N and 4N are acted on a body. The ratio of magnitude of minimum and maximum resultant force on the body is
3/4
4/3
1/7
none of these
To solve the problem, we need to determine the minimum and maximum resultant forces when two forces of magnitudes 3N and 4N are acting on a body.
1. Identify the Forces: We have two forces, F1=3N and F2=4N.
2. Determine Maximum Resultant Force:
- The maximum resultant force occurs when the two forces are acting in the same direction (0 degrees between them).
- The formula for the maximum resultant force Fmax is:
Fmax=F1+F2
- Substituting the values:
Fmax=3N+4N=7N
3. Determine Minimum Resultant Force:
- The minimum resultant force occurs when the two forces are acting in opposite directions (180 degrees between them).
- The formula for the minimum resultant force Fmin is:
Fmin=|F1−F2|
- Substituting the values:
Fmin=|3N−4N|=|−1N|=1N
4. Calculate the Ratio of Minimum to Maximum Resultant Force:
- The ratio of the minimum resultant force to the maximum resultant force is given by:
Ratio=FminFmax
- Substituting the values:
Ratio=1N7N=17
Final Answer:
The ratio of the magnitude of minimum and maximum resultant force on the body is 17.
- The maximum resultant force occurs when the two forces are acting in the same direction (0 degrees between them).
- The formula for the maximum resultant force Fmax is:
Fmax=F1+F2
- Substituting the values:
Fmax=3N+4N=7N
- The minimum resultant force occurs when the two forces are acting in opposite directions (180 degrees between them).
- The formula for the minimum resultant force Fmin is:
Fmin=|F1−F2|
- Substituting the values:
Fmin=|3N−4N|=|−1N|=1N
- The ratio of the minimum resultant force to the maximum resultant force is given by:
Ratio=FminFmax
- Substituting the values:
Ratio=1N7N=17
The ratio of the magnitude of minimum and maximum resultant force on the body is 17.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Two non-collinear forces, one of 10 N and another of 6 N act upon a body. The directions of the forces are unknown. The resultant force on the body is :
Abetween 6 and 10 NBbetween 4 and 16 NCmore than 6 NDmore than 10 NTwo forces of 12N and 8N act upon a body. The resultant force on the body maximum value of
A4NB0NC20ND8N
Two forces of magnitudes 3N and 4N respectively are acting on a body. Calculate the resultant force if the angle between them is : (i) 0∘ (ii) 180∘ (iii) 90∘
View SolutionTwo forces of magnitudes 3N and 4N respectively are acting on a body. Calculate the resultant force if the angle between them is-
(i)0∘ (ii)180∘ (iii)90∘
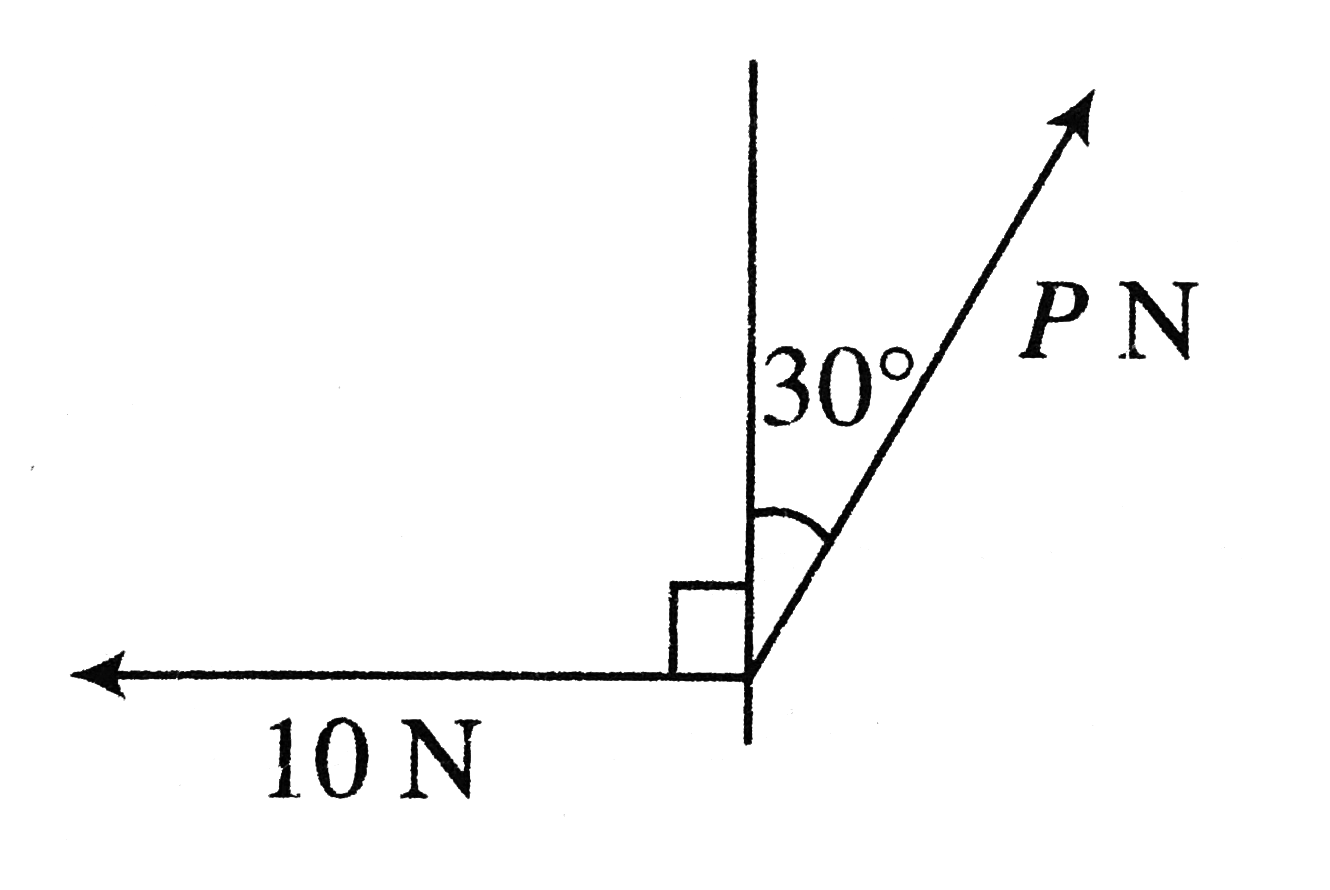
View SolutionTwo horizontal forces of magnitudes of 10N and PN act on a particle. The force of magnitude 10N acts due west and the force of magnitude PN acts on a bearing of 30∘ east of north as shown in (figure) The resultant of these two force acts due north. Find the magnitude of the resultant.
View SolutionTwo forces of magnitudes 3N and 4 N act together on an object making an angle 60∘ with each other. Find the resultant force acting on the object.
View SolutionForces of magnitudes 6N and 4N are acting on the body . Which of the following of the following can be the resultant of the two?
(a) 11N (b) 2N (c) 10N (d) 1N (e) 8N (f) 0N (g) 7N
View SolutionTwo forces of magnitude 3N and 4N respectively are acting on a body. Calculate the resultant force if the angle between them is
0∘
View Solution
