Two identical coils are placed coaxially. They carry equal currents in same direction
NOTE in parts (a), (b) and (c) exclude the points at infinity.
(a)on their axis there are two points where net magnetic field is zero
(b)on their axis there are three points where net magnetic field is zero
(c)on their axis there is no such point where net magnetic field is zero
(d)on moving from the centre of one coil to the other, magnetic field will first decrease then increase
The correct Answer is:c
To solve the problem of two identical coils placed coaxially carrying equal currents in the same direction, we will analyze the magnetic field created by these coils and determine if there are any points along the axis where the net magnetic field is zero.
1. Understanding the Setup:
- We have two identical coils placed one above the other, and they are coaxial.
- Both coils carry equal currents in the same direction.
2. Direction of Magnetic Field:
- According to the right-hand rule, if the current in both coils flows in the same direction (let's assume clockwise when viewed from one end), the magnetic field produced by each coil will also point in the same direction along the axis of the coils.
- Therefore, at any point along the axis of the coils, the magnetic fields due to both coils will be in the same direction.
3. Analyzing Points Along the Axis:
- The magnetic field due to a single coil at a point along its axis can be calculated using the formula:
B=μ0nI2R(1−z√z2+R2)
where B is the magnetic field, I is the current, R is the radius of the coil, z is the distance from the center of the coil along the axis, and n is the number of turns.
- For two coils, the total magnetic field at any point on the axis is simply the sum of the magnetic fields due to each coil.
4. Finding Points of Zero Magnetic Field:
- Since both coils produce magnetic fields in the same direction, the magnetic fields will add up at every point along the axis.
- Therefore, there cannot be a point along the axis where the magnetic fields from both coils cancel each other out.
5. Conclusion:
- Since the magnetic fields from both coils are always in the same direction and add up, there are no points along the axis where the net magnetic field is zero.
- Thus, the answer to the question is that there is no such point on the axis where the net magnetic field is zero.
Final Answer:
There is no point on the axis where the magnetic field is zero.
---
- We have two identical coils placed one above the other, and they are coaxial.
- Both coils carry equal currents in the same direction.
- According to the right-hand rule, if the current in both coils flows in the same direction (let's assume clockwise when viewed from one end), the magnetic field produced by each coil will also point in the same direction along the axis of the coils.
- Therefore, at any point along the axis of the coils, the magnetic fields due to both coils will be in the same direction.
- The magnetic field due to a single coil at a point along its axis can be calculated using the formula:
B=μ0nI2R(1−z√z2+R2)
where B is the magnetic field, I is the current, R is the radius of the coil, z is the distance from the center of the coil along the axis, and n is the number of turns.
- For two coils, the total magnetic field at any point on the axis is simply the sum of the magnetic fields due to each coil.
- Since both coils produce magnetic fields in the same direction, the magnetic fields will add up at every point along the axis.
- Therefore, there cannot be a point along the axis where the magnetic fields from both coils cancel each other out.
- Since the magnetic fields from both coils are always in the same direction and add up, there are no points along the axis where the net magnetic field is zero.
- Thus, the answer to the question is that there is no such point on the axis where the net magnetic field is zero.
There is no point on the axis where the magnetic field is zero.
Topper's Solved these Questions
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Comprehension type Questions
16 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Matrix Matching type Questions
12 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Only One Option is Correct
45 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
- MEASUREMENT AND ERRORSBOOK - DC PANDEY ENGLISHCHAPTER - MEASUREMENT AND ERRORSEXERCISE - Subjective
19 Videos
Similar Questions
Assertion Two infinitely long wires A and B carry unequal currents both in inward direction.

Then, there is only point (excluding the ponts at infinity), where net magnetic field is zero.
Reason That point lies between points A and B.
View SolutionTwo circular, similar, coaxial loops carry equal currents in the same direction. If the loops are brought nearer, what will happen?
View Solution
Knowledge Check
Two circular, similar, coaxial loops carry equal currents in the same direction. If the loops are brought nearer, what will happen?
AP increases while in Q decreasesBQ increases while in P decreasesCboth P and Q increasesDboth P and Q decreases
Two identical coaxial circular loops carry a current i each circulating int the same direction. If the loops approch each other the current in
View SolutionThe figure shows the cross section of two long coaxial tubes carrying equal current I in opposites directions. If B1 and B2 are magnetic fields at point 1 and 2 as shown in figure then

View SolutionTwo long parallel wires carry equal current I flowing in the same direction are at a distance 2d apart. The magnetic field B at a point lying on the perpendicular line joining the wires and at a distance x from the midpoint is
View SolutionTwo circular coils P & Q are coaxially & carry currents I1 and I2 respectively (all direction are w.r.t. the observer)

View SolutionThree identical circular coils A, B and C are placed coaxial (with planes parallel to each other) The coils A and C equal currents in opposite direction as shown. The coils B and C are fixed in positions and the coil A is moved towards B wiyj uniform motion then -
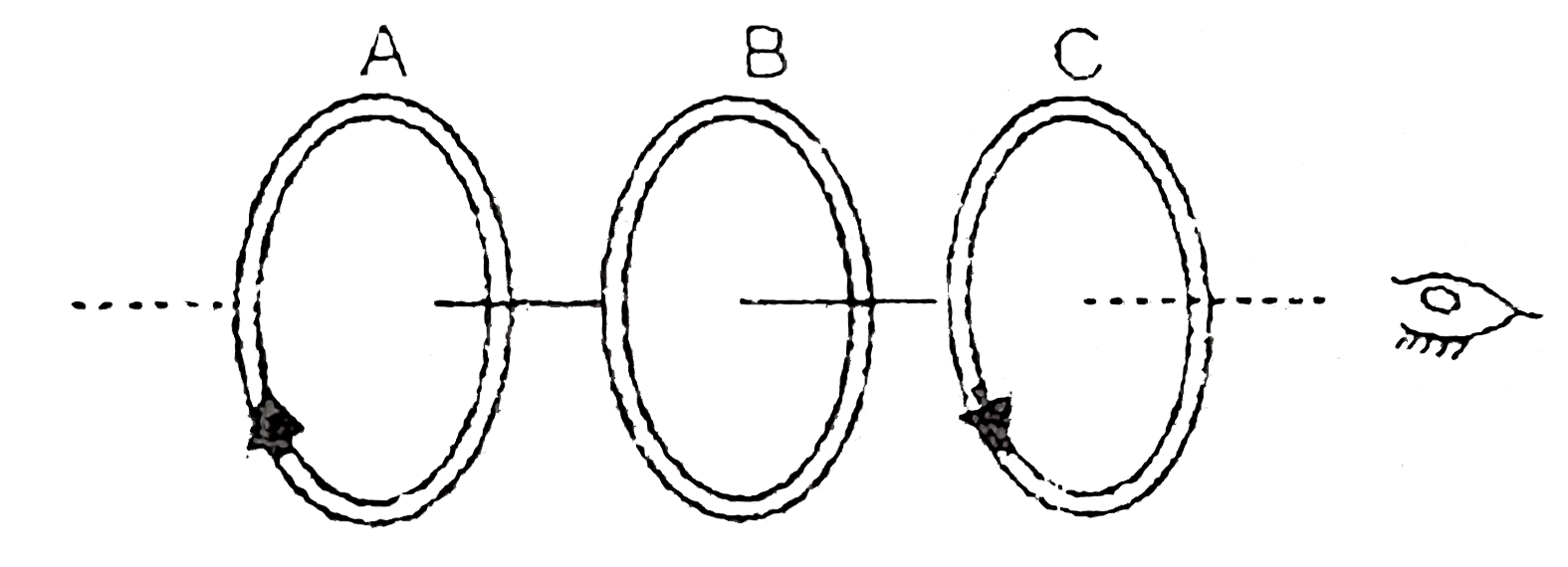
View SolutionA wire is parallel to a square coil . The coil and wire carry currents in the directions Shown . Then, at any point A within the coil the magnetic field will be -

View SolutionTwo parallel wires carry equal currents of 10A along the same direction and are separated by a distance of 2.0 cm. Find the magnetic field at a point which is 2.0 cm away from each of these wires.
View Solution
