Two identical discs of same radius R are rotating about their axes in opposite directions with the same constant angular speed ω . The discs are in the same horizontal plane. At time t=0 , the points P and Q are facing each other as shown in the figure. The relative speed between the two points P and Q is vr. In one time period (T) of rotation of the discs , vr as a function of time is best represented by
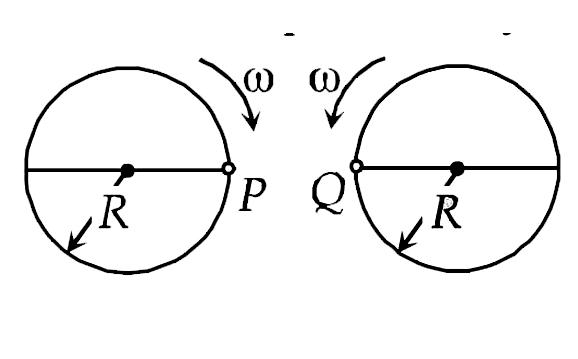


The correct Answer is:A
At an instant, speed of P=v, going in clockwise direction
Speed of Q=v, going in anticlockwise direction
Relative angular velocity of Pw.r.tQ=ω−(−ω)=2ω
Relative angualr separation of P and Q in time tθ=2ωt.
Relative speed between the points P and Q at time t
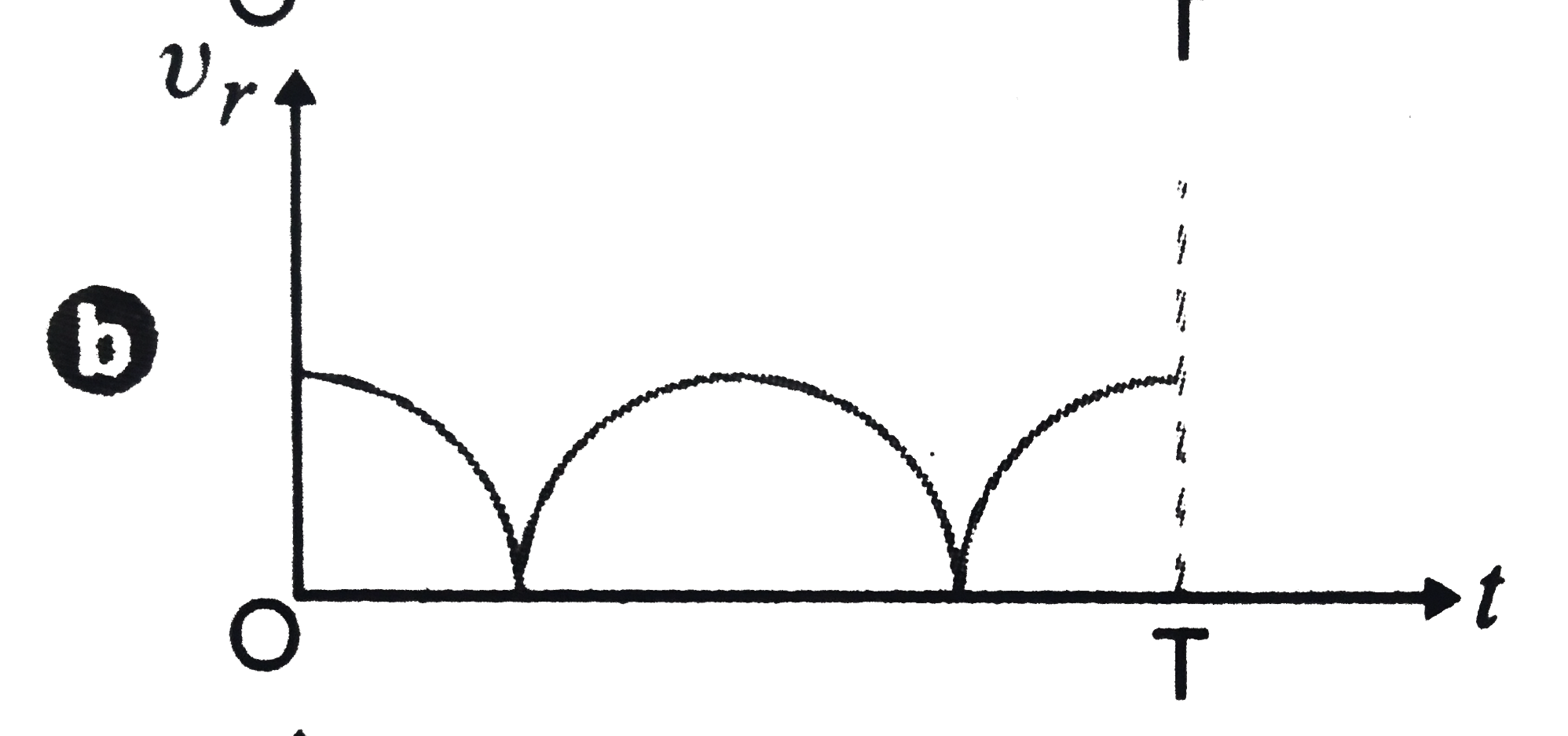
∣∣→υr∣∣=√υ2+υ2−2υυcos(2ωt)
=√2υ2(1−cos2ωt)=√2υ2×2sin2ωt
=2υsinωt
Since ∣∣→υr∣∣ will not have negative value so the lower part of the sine wave will come upper side. Hence option (a) is true.
Similar Questions
A disc of radius R start at time t=0 moving along the positive X-axis with linear speed b and angular speed ω. Find the x and y-coordinates of the bottommost point at any time t.

View Solution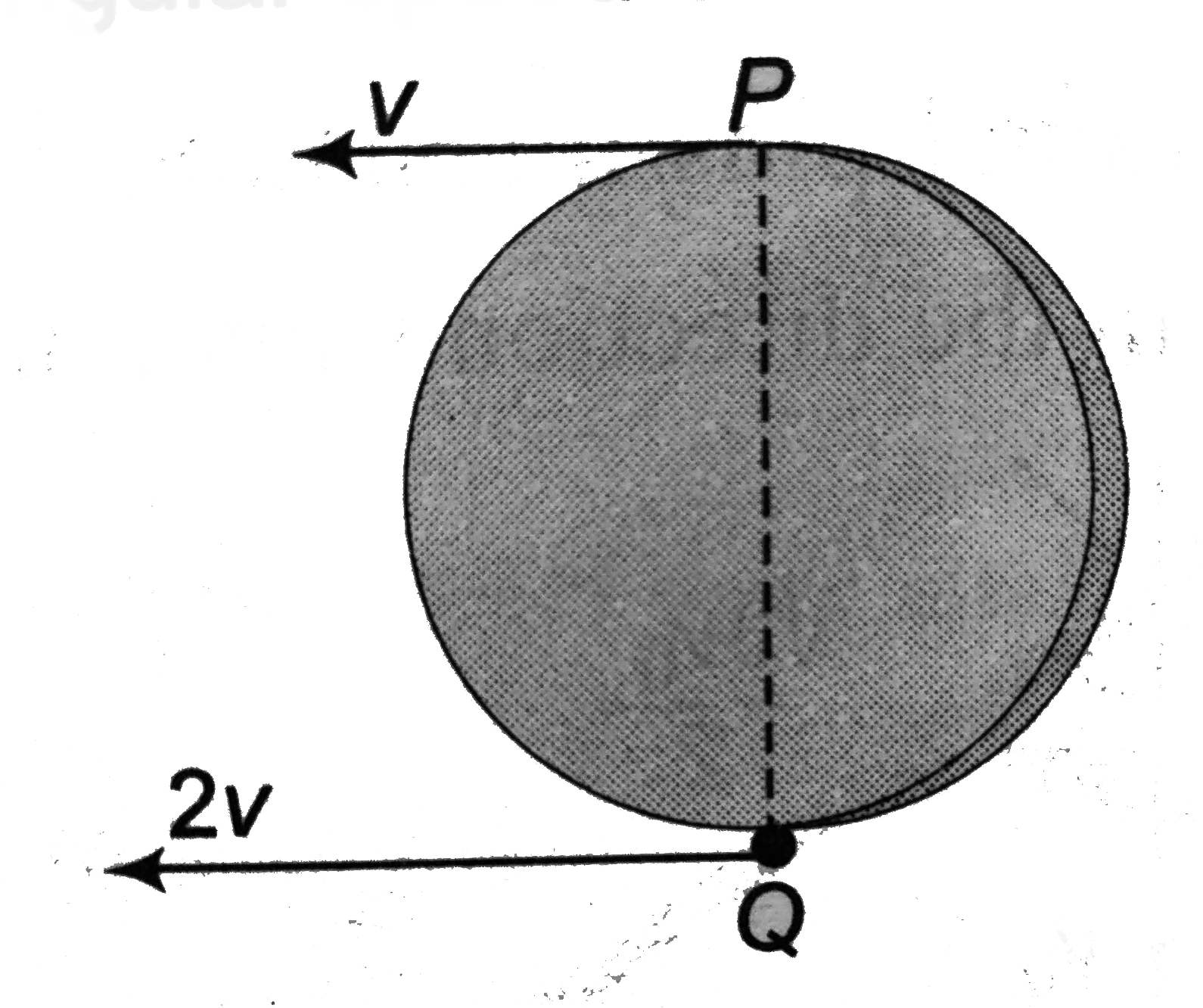
Two point P and Q. diametrically opposite on a disc of radius R have linear velocities v and 2v as shown in figure. Find the angular speed of the disc.
View Solution
Knowledge Check
Two particles P and Q are moving as shown in the figure. At this moment of time the angular speed of P w.r.t. Q is
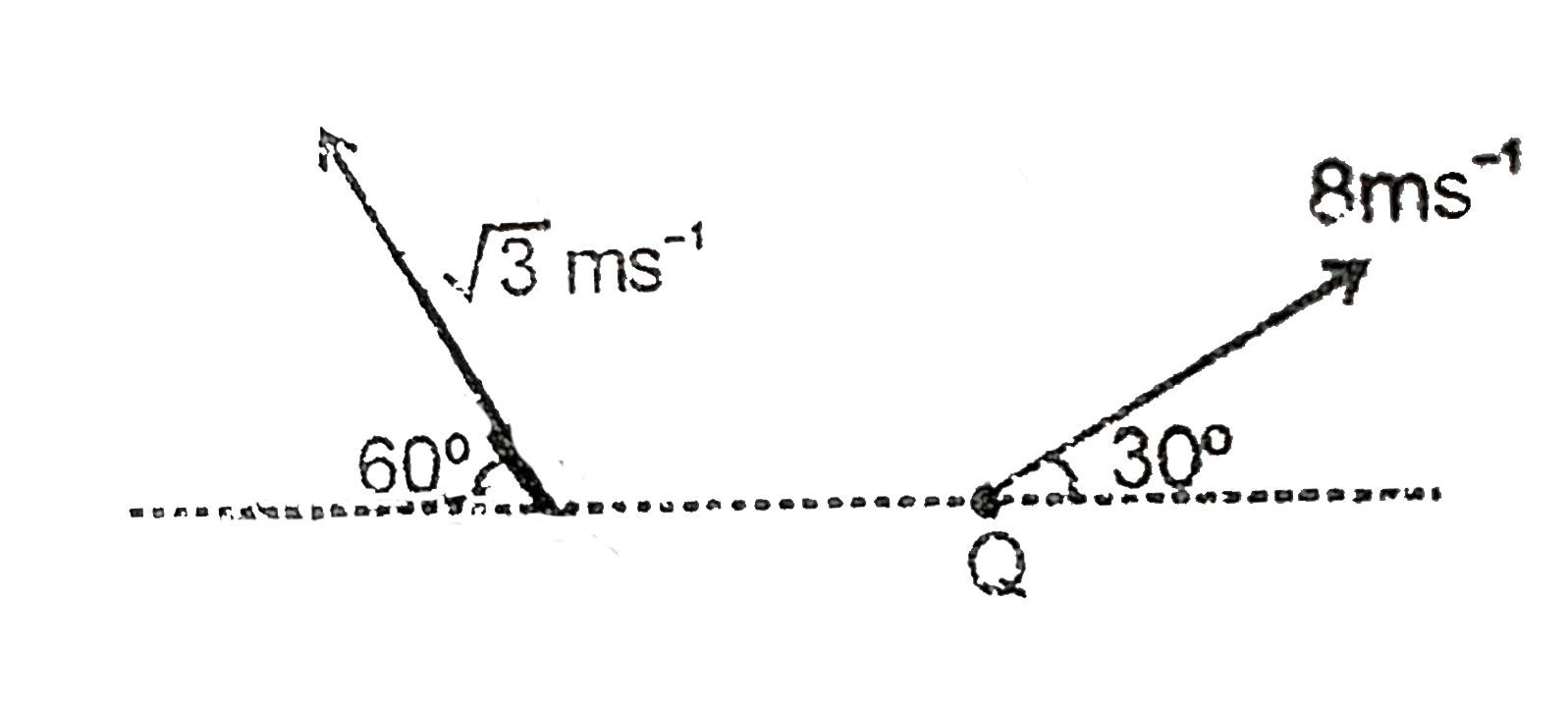 A5 rads−1B4 rads−1C2 rads−1D1 rads−1
A5 rads−1B4 rads−1C2 rads−1D1 rads−1Two cars are moving is one a same line dimension in opposite direction with the same speed v. The relative velocity of two cars w.r.t. each other is
A2 vBvCv2DZeroA disc is freely rotating with an angular speed ω on a smooth horizontal plane. If it is hooked at a rigid pace P and rotates without bouncing about a point on its circumference. Its angular speed after the impact will be equal to.
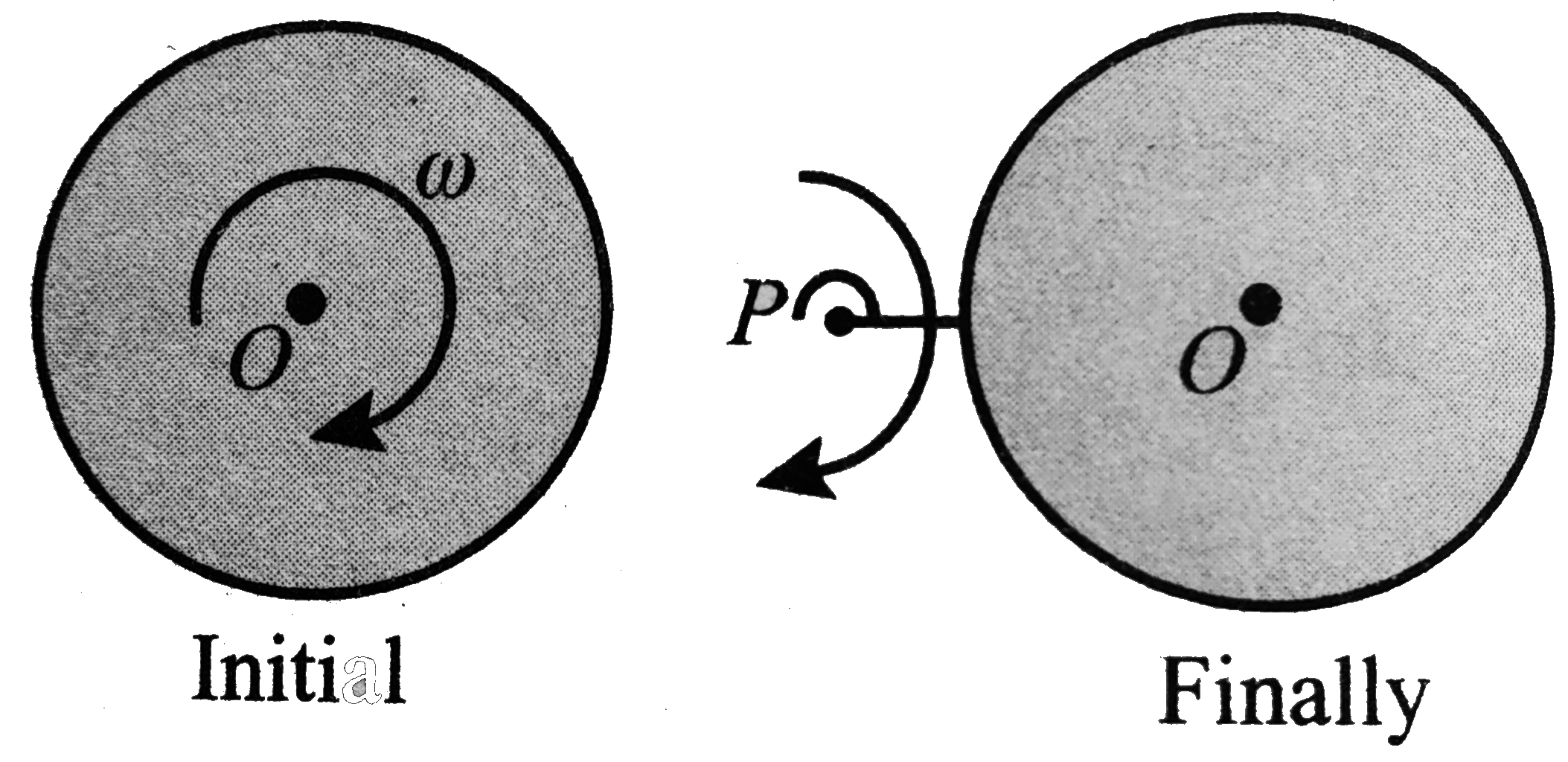 A2ω3Bω3Cω2Dnone of the above
A2ω3Bω3Cω2Dnone of the above
A disc of radius R is moving on a rough horizontal surface with velocity v and angular speed ω at an instant as shown in figure. Choose the correct statement.

View SolutionConsider a disc rotating in the horizontal plane with a constant angular speed ω about its centre O . The disc has a shaded region on one side of the diameter and an unshaded region on the other side as shown in the figure. When the disc is in the orientation as shown, two pebbles P and Q are simultaneously projected at an angle towards R. The velocity of projection is in the y-z plane and is same for both pebbles with respect to the disc. Assume that (i) they land back on the disc before the disc has completed 18 rotation, (ii) their range is less than half the disc radius, and (iii) w remains constant throughout. Then
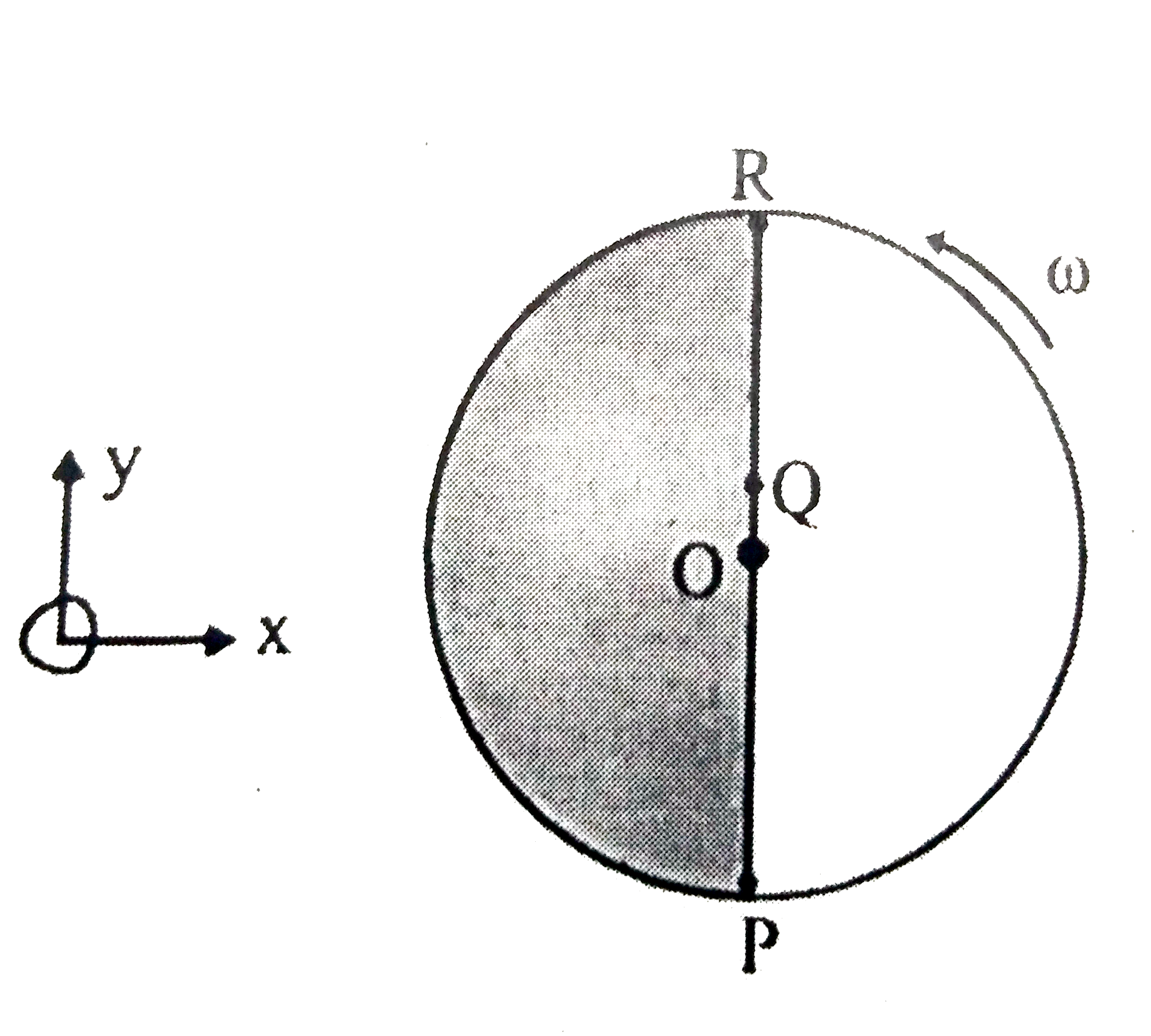
View SolutionConsider a disc rotating in the horizontal plane with a constant angular speed ω about its centre O . The disc has a shaded region on one side of the diameter and an unshaded region on the other side as shown in the figure. When the disc is in the orientation as shown, two pebbles P and Q are simultaneously projected at an angle towards R. The velocity of projection is in the y-z plane and is same for both pebbles with respect to the disc. Assume that (i) they land back on the disc before the disc has completed 18 rotation, (ii) their range is less than half the disc radius, and (iii) w remains constant throughout. Then

View SolutionAn electron is at P t=0 It is circulating in anticlockwise direction with a constant angular speed ω along the shown circular path. Magnetic field at Q(CQ=2R, where R is radius of the circular) will be recorded as zero at times)

View SolutionA circular disc of radius R is rotating about its axis O with a uniform angular velocity ωrad s−1 as shown in the figure. The magnitude of the relative velocity of point A relative to point B on the disc is

View Solution
