Two identical disks A and B can spin around vertical axes. Disk A is spinning with an initial angular speed of 40 rev/s when its rim touches initially stationary disk B, causing that disk to begin to spin. The rubbing at the contact point slows A while speeding up B. The rate at which both disks change their angular speeds is 2.0rev/s2. Find the time required for the two disks to reach the same angular speed.
To solve the problem, we need to find the time required for the two disks A and B to reach the same angular speed after they start rubbing against each other.
Step 1: Define the initial conditions.
- Disk A has an initial angular speed ωA=40rev/s.
- Disk B is initially stationary, so ωB=0rev/s.
- The rate at which both disks change their angular speeds is given as 2.0rev/s2.
Step 2: Write the equations for the angular speeds of both disks over time.
- The angular speed of disk A after time t can be expressed as:
ωA(t)=ωA−2t=40−2t
- The angular speed of disk B after time t can be expressed as:
ωB(t)=ωB+2t=0+2t=2t
Step 3: Set the equations equal to find when both disks have the same angular speed.
- We need to find the time t when ωA(t)=ωB(t):
40−2t=2t
Step 4: Solve for t.
- Rearranging the equation gives:
40=2t+2t
40=4t
t=404=10seconds
Step 5: Conclusion
- The time required for the two disks to reach the same angular speed is t=10seconds.
---
- Disk A has an initial angular speed ωA=40rev/s.
- Disk B is initially stationary, so ωB=0rev/s.
- The rate at which both disks change their angular speeds is given as 2.0rev/s2.
- The angular speed of disk A after time t can be expressed as:
ωA(t)=ωA−2t=40−2t
- The angular speed of disk B after time t can be expressed as:
ωB(t)=ωB+2t=0+2t=2t
- We need to find the time t when ωA(t)=ωB(t):
40−2t=2t
- Rearranging the equation gives:
40=2t+2t
40=4t
t=404=10seconds
- The time required for the two disks to reach the same angular speed is t=10seconds.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)43videos
RIGID BODY DYNAMICS - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)7videos
RIGID BODY DYNAMICS - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - CHECKPOINT18videos
RIGID BODY DYNAMICS - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - RELATIVITYEXERCISE - PRACTICE QUESTIONS (Integer Type)5videos
RELATIVITY
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)2videos
RIGID BODY DYNAMICS-II
Similar Questions
Knowledge Check
- Question 1 - Select One
A circular disk of radius 0.010 m rotates with a constant angular speed of 5.0 rev/s. What is the acceleration of a point on the edge of the disk?
A0.31m/s2B9.9m/s2Czero m/s2D1.6m/s2 - Question 2 - Select One
A circular disk of radius 2.0 m rotates, starting from rest, with a constant angular acceleration of 20.0rad/s2. What is the tangential acceleration of a point on the edge of the disk at the instant that its angular speed is 1.0 rev/s?
A40m/s2B110m/s2C79m/s2D120m/s2 - Question 3 - Select One
By viewing the properties of the local hard disk of a computer, the user can find out
Athe amount of space that has been used up and the remaining free space on the diskBthe name of the user viewing the properties of the diskCnothing useful to the user.Dthe number of programs available in the computer
Calculate the volume of given disk.
 View Solution
View SolutionA uniform disk of mass 300kg is rotating freely about a vertical axis through its centre with constant angular velocity ω. A boy of mass 30kg starts from the centre and moves along a radius to the edge of the disk. The angular velocity of the disk now is
View SolutionA disk A of radious r moving on perfectly smooth surface at a speed v undergoes an elastic collision with an identical stationary disk B. Find the velocity of the disk B after collision if the impact parameter is r/2 as shown in the figure :-
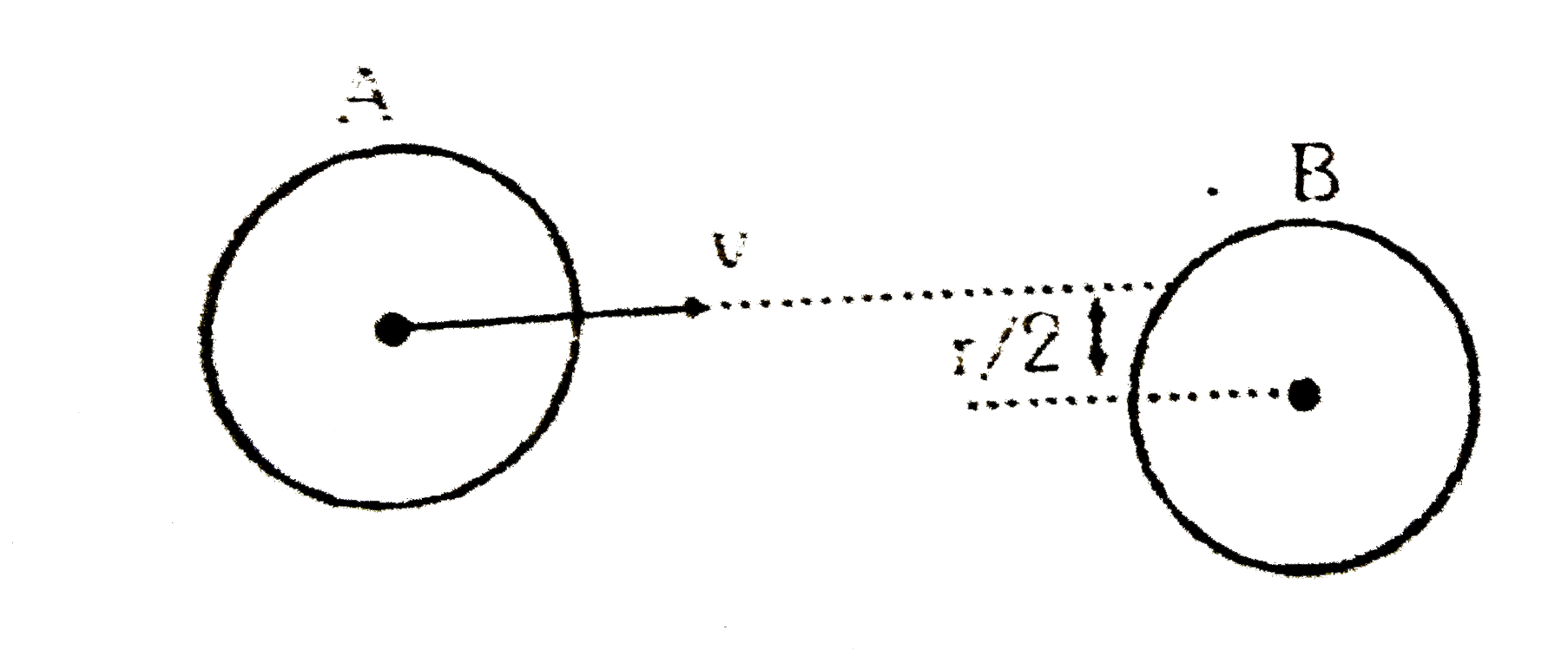 View Solution
View SolutionA positively charged disk is rotated clockwise as shown in Fig. The direction of hte magnetic field at a point A in the plane of the disk is
View SolutionA circular disk of moment of inertia It is rotating in a horizontal plane , about its symmetry axis , with a constant angular speed ωi . Another disk of moment of inertia Ib is dropped coaxially onto the rotating disk . Initially the second disk has zero angular speed . eventually both the disks rotate with a constant angular speed ωf . The energy lost by the initially rotating disc to friction is
View Solution