Two identical masses are connected to a horizontal thin massless rod as shown in the figure. When their distance from the pivot is x, a torque produces an angular acceleration α1. If the masses are now repositioned so that they are at distance 2x each from the pivot, the same torque will produce an angular acceleration α2 such that ,

α2=4α1
α2=α1
α2=α12
α2=α14
The correct Answer is:D
τ=(2mx2)α1
=(2×m×4x2)α2
Equating 8mx2α1 or α2=α14
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Multiple Correct
9 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Linked Comprehension
28 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Subjective
13 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
Two uniform thin rods each of length L and mass m are joined as shown in the figure. Find the distance of centre of mass the system from point O

View SolutionTwo equal and opposite forces are allplied tangentially to a uniform disc of mass M and radius R as shown in the figure. If the disc is pivoted at its centre and free to rotate in its plane, the angular acceleration of the disc is :

View Solution
Knowledge Check
A particle is at a distance r from the axis of rotation. A given torque τ produces some angular acceleration in it. If the mass of the particle is doubled and its distance from the axis is halved, the value of torque to produce the same angular acceleration is -
Aτ/2BτC2τD4τTwo identical thin uniform rods of length L each are joined to form T shape as shown in the figure. The distance of centre of mass from D is
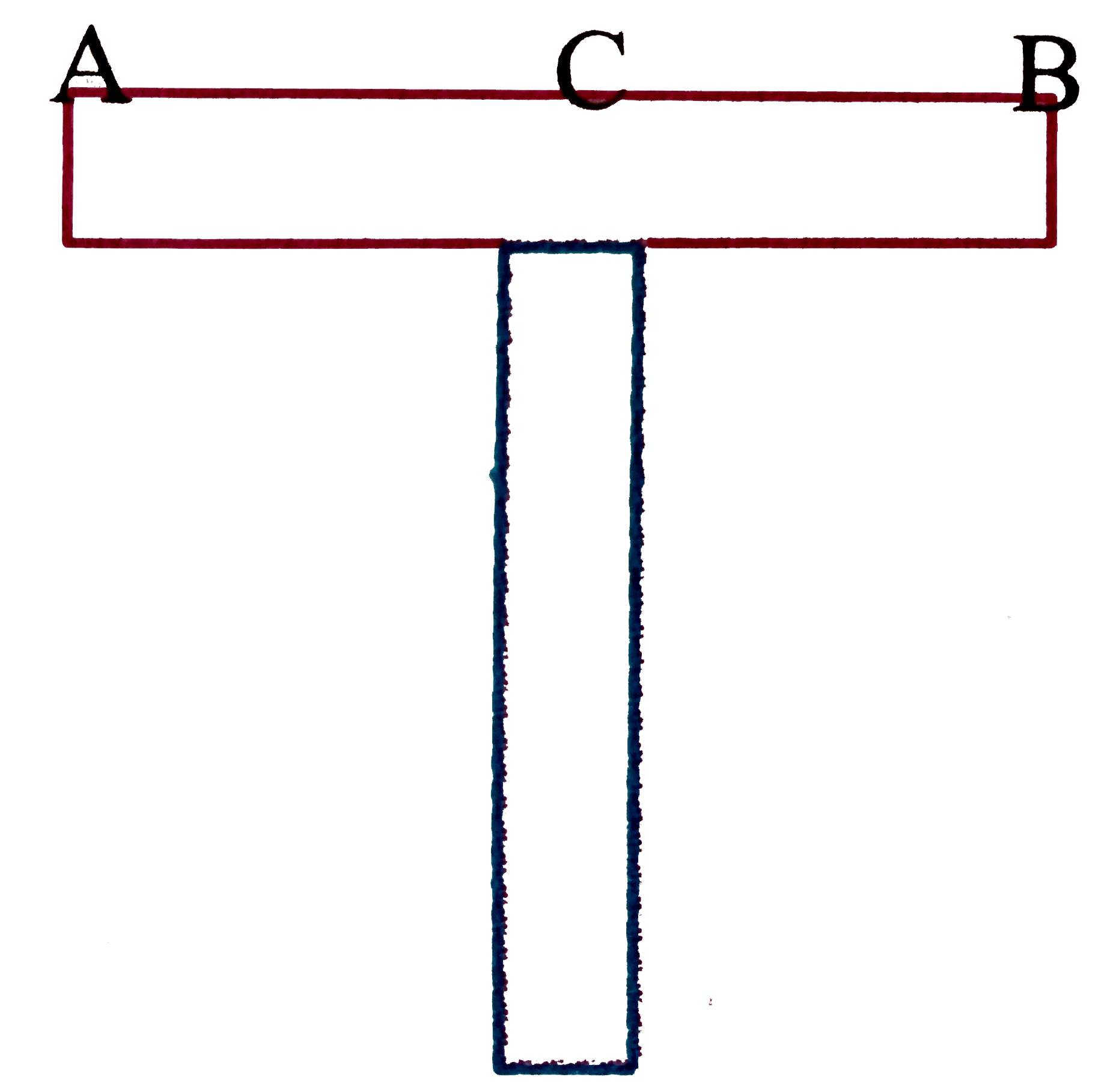 A0BL/4C3L/4DL
A0BL/4C3L/4DLA rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a massless string tied to point Q as shown in figure. When string is cut, the intial angular acceleration of the rod is
 A3g2LBgLC2gLD2g3L
A3g2LBgLC2gLD2g3L
A uniform thin rod is released from rest in the horizontal position as shown in the figure. For what value of x, the angular acceleration is maximum.
View SolutionA torque of 2 newton-m produces an angular acceleration of 2rad/sec2 a body. If its radius of gyration is 2m, its mass will be:
View SolutionTwo masses are attached to a rod end to end . If torque is applied they rotate with angular acceleration α. If their distances are doubled and same torque is applied, then they move with angular acceleration.
View SolutionA system consists of two masses connected by a massless rod lies along x-axis. The distance of centre of mass from O is
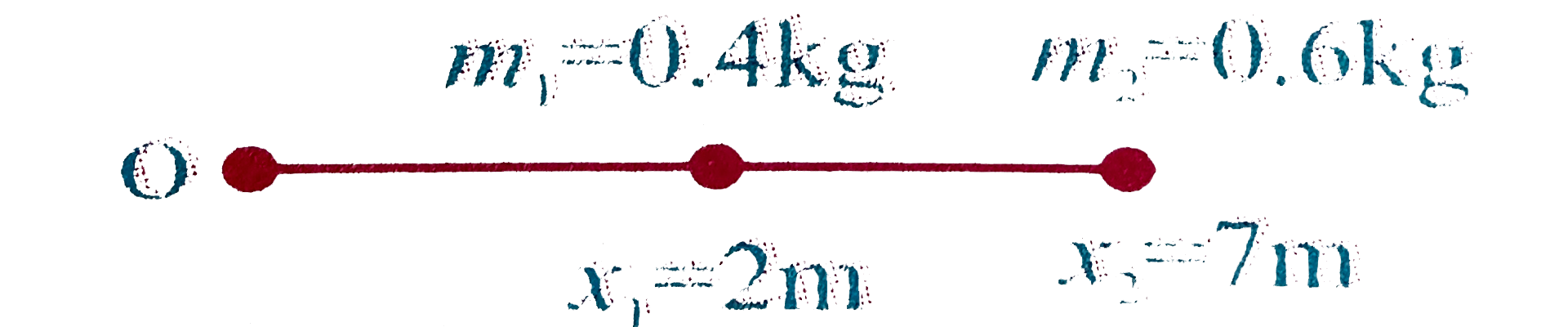
View SolutionIf a wheel has mass 70 kg and radius of gyration 1 m, then the torque required an angular 1 m, then the torque required an angular acceleration of 2 rev/s2 will be
View Solution
