Two identical positive charges are fixed on the y-axis, at equal distances from the origin O. A particle with a negative charges starts on the x-axis at a large distance from O. moves along the x-axis passes through O, and moves far away from O on the other side. Its acceleration a is taken as positive along its direction of motion. Plot acceleration a of the particle against its x-coordinate.
To solve the problem, we need to analyze the forces acting on the negatively charged particle as it moves along the x-axis in the presence of two identical positive charges located on the y-axis. We will plot the acceleration of the particle against its x-coordinate.
1. Understanding the Setup:
- We have two identical positive charges, let's say +Q, located at (0, d) and (0, -d) on the y-axis.
- A negative charge, -q, starts from a large distance on the x-axis, moves through the origin (0, 0), and continues to the negative x-axis.
2. Force Calculation:
- The force on the negative charge due to each positive charge can be calculated using Coulomb's Law:
F=k|q1q2|r2
- Here, k is Coulomb's constant, q1 and q2 are the magnitudes of the charges, and r is the distance between the charges.
3. Acceleration Calculation:
- The net force acting on the negative charge is the vector sum of the forces due to both positive charges.
- Since the negative charge is moving along the x-axis, we only need to consider the x-components of the forces from the two positive charges.
- The acceleration a of the negative charge can be calculated using Newton's second law:
a=Fnetm
- Where m is the mass of the negative charge.
4. Behavior of Acceleration:
- As the negative charge approaches the origin from the positive side of the x-axis, the forces from both positive charges will attract it towards the origin, resulting in a maximum acceleration.
- At the origin (x = 0), the forces from both charges cancel each other out, leading to zero acceleration.
- As the charge moves to the negative side of the x-axis, the same behavior occurs: it experiences a force towards the origin, resulting in negative acceleration but still positive in the direction of motion.
5. Plotting the Graph:
- On the graph, the x-axis will represent the x-coordinate of the particle, and the y-axis will represent the acceleration a.
- Starting from a large positive x, the acceleration will be positive and decrease as the particle approaches the origin, reaching zero at the origin.
- After passing through the origin, the acceleration will again become positive but will decrease in magnitude as the particle moves further into the negative x-axis.
Final Graph:
- The graph of acceleration a vs. x-coordinate will show:
- A curve starting from a positive value at large positive x, decreasing to zero at x = 0, and then becoming negative as it moves into the negative x-axis, eventually approaching zero again as it moves far away on the negative side.
- We have two identical positive charges, let's say +Q, located at (0, d) and (0, -d) on the y-axis.
- A negative charge, -q, starts from a large distance on the x-axis, moves through the origin (0, 0), and continues to the negative x-axis.
- The force on the negative charge due to each positive charge can be calculated using Coulomb's Law:
F=k|q1q2|r2
- Here, k is Coulomb's constant, q1 and q2 are the magnitudes of the charges, and r is the distance between the charges.
- The net force acting on the negative charge is the vector sum of the forces due to both positive charges.
- Since the negative charge is moving along the x-axis, we only need to consider the x-components of the forces from the two positive charges.
- The acceleration a of the negative charge can be calculated using Newton's second law:
a=Fnetm
- Where m is the mass of the negative charge.
- As the negative charge approaches the origin from the positive side of the x-axis, the forces from both positive charges will attract it towards the origin, resulting in a maximum acceleration.
- At the origin (x = 0), the forces from both charges cancel each other out, leading to zero acceleration.
- As the charge moves to the negative side of the x-axis, the same behavior occurs: it experiences a force towards the origin, resulting in negative acceleration but still positive in the direction of motion.
- On the graph, the x-axis will represent the x-coordinate of the particle, and the y-axis will represent the acceleration a.
- Starting from a large positive x, the acceleration will be positive and decrease as the particle approaches the origin, reaching zero at the origin.
- After passing through the origin, the acceleration will again become positive but will decrease in magnitude as the particle moves further into the negative x-axis.
- The graph of acceleration a vs. x-coordinate will show:
- A curve starting from a positive value at large positive x, decreasing to zero at x = 0, and then becoming negative as it moves into the negative x-axis, eventually approaching zero again as it moves far away on the negative side.
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Subjective Type
15 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Subjective
32 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Solved examples
10 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
Similar Questions
A particle is moving along the x-axis and its position-time graph is shown. Determine the sign of acceleration.
View SolutionA point lies on negative direction of X-axis at a distance 6 units from Y-axis. What are its coordinates ?
View SolutionFind the locus of the point such that its distance from the x-axis is half its distance from the y-axis.
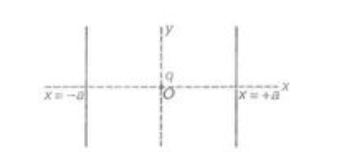
View SolutionTwo identical infinite positive line changes are places into the lines x=±a in the x=y plane. A positive point charge placed at origin is restricted to move along x-axis its equilibrium is
View SolutionFind the locus of a point which moves such that its distance from the origin is three times its distance from x-axis.
View SolutionFind the equation of the locus of a point which moves so that its distance from the x-axis is double of its distance from the y-axis.
View SolutionA body starts from the origin with an acceleration of 6ms−2 along the x - axis and 8ms−2 along the y - axis. Find its distance from the origin after 4s.
View SolutionFind the locus of a point which moves so that its distance from the x-axis is twice its distance from the y-axis.
View SolutionA point lies on positive direction of X-axis at a distance of 7 units from the Y-axis . What are its coordinates? What will be the coordinates, if it lies on negative direction of Y-axis at a distance of 7 units from X-axis ?
View SolutionA body starts from origin and moves along x - axis so that its position at any instant is x=4t2−12t where t is in second. What is the acceleration of particle?
View Solution