Two identical springs, each of force constant k are connected I (a) series (b) parallel and they support a mass M. Calculate the ratio of the frequency of oscillation of the mass in two systems.
1:1
1:2
2:1
4:1
The correct Answer is:C
When they are joined in series, the effective force constant is (K/2) and when they are joined in parallel, the force constant is 2K.
ω=√Km∴2πT=√Km∴T=2π√mK
∴T1T2=2π2π√mK/2×2Km=√4=2
∴T1=2T2
Topper's Solved these Questions
Similar Questions
Two identical spring of constant K are connected in series and parallel as shown in figure. A mass mis suspended from them. The ratio of their frequencies of vertical oscillations will be
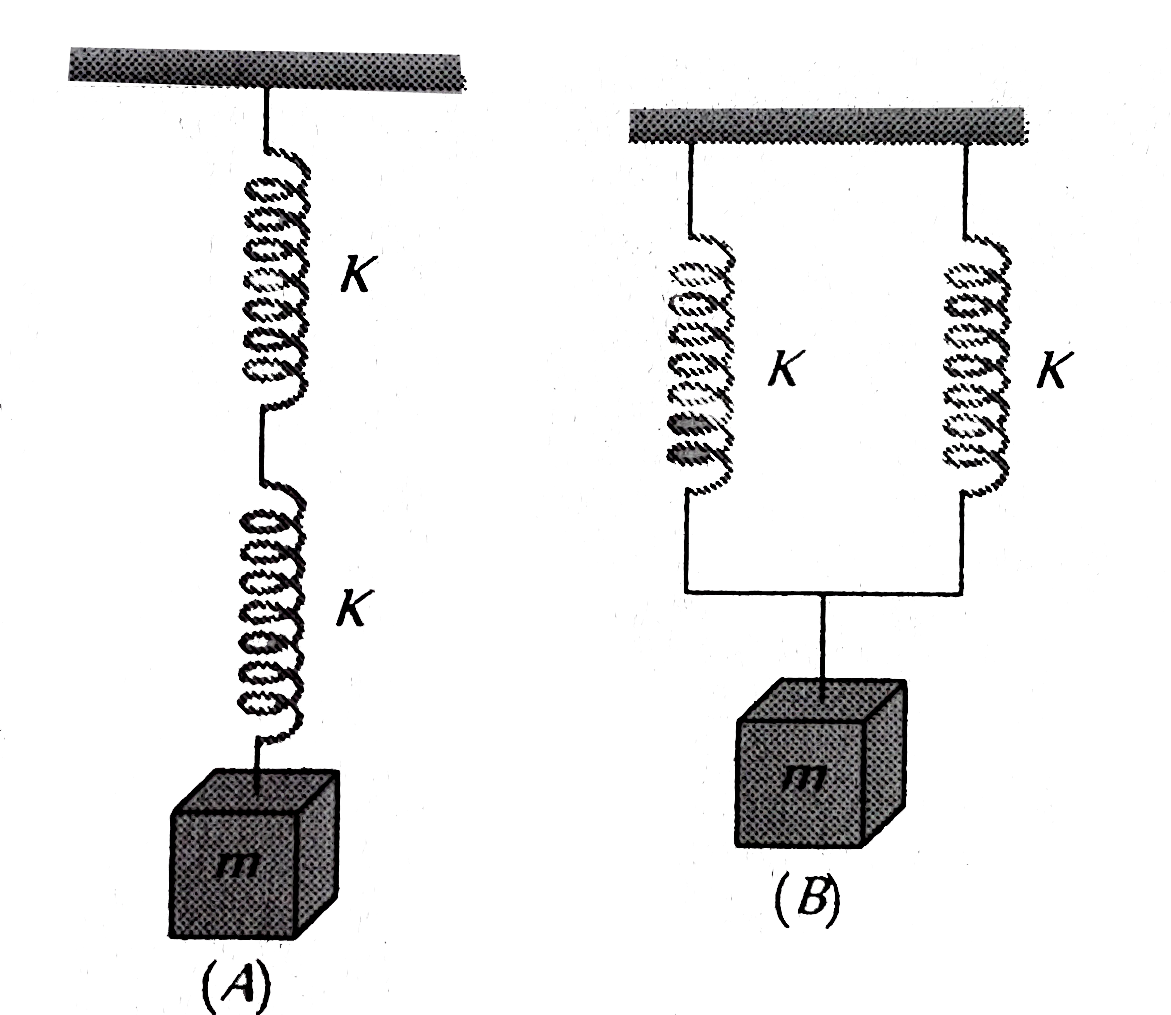
View SolutionTwo spring of spring constants k1 and k2 ar joined and are connected to a mass m as shown in the figure. Calculate the frequency of oscillation of mass m.

View Solution
Knowledge Check
Two identical springs of spring constant k each are connected in series and parallel as shown in figure. A mass M is suspended from them. The ratio of their frequencies of vertical oscillation will be
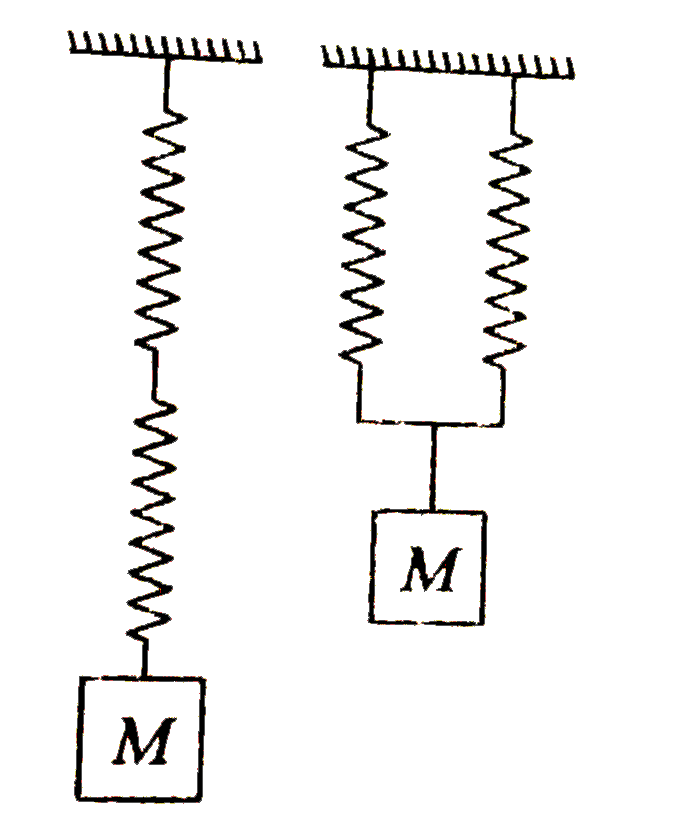 A1:2B2:1C4:1D1:4
A1:2B2:1C4:1D1:4Two spring of each force constant k is connected in series and parallel combination is provided with mass m. The ratio of time periods of these two combination is
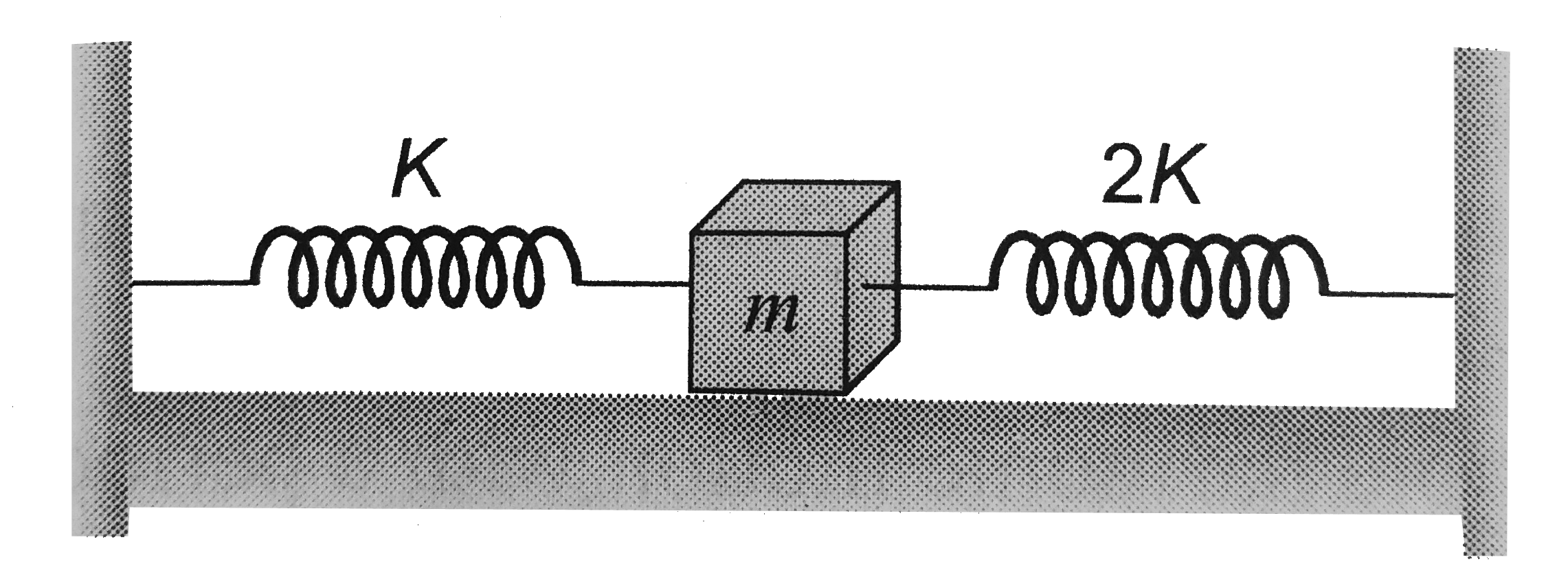
A2:1B1:√2C√2:0.5D√2:1Two springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is
 A12π√mkB12π√2kmC12π√3kmD12π√mk
A12π√mkB12π√2kmC12π√3kmD12π√mk
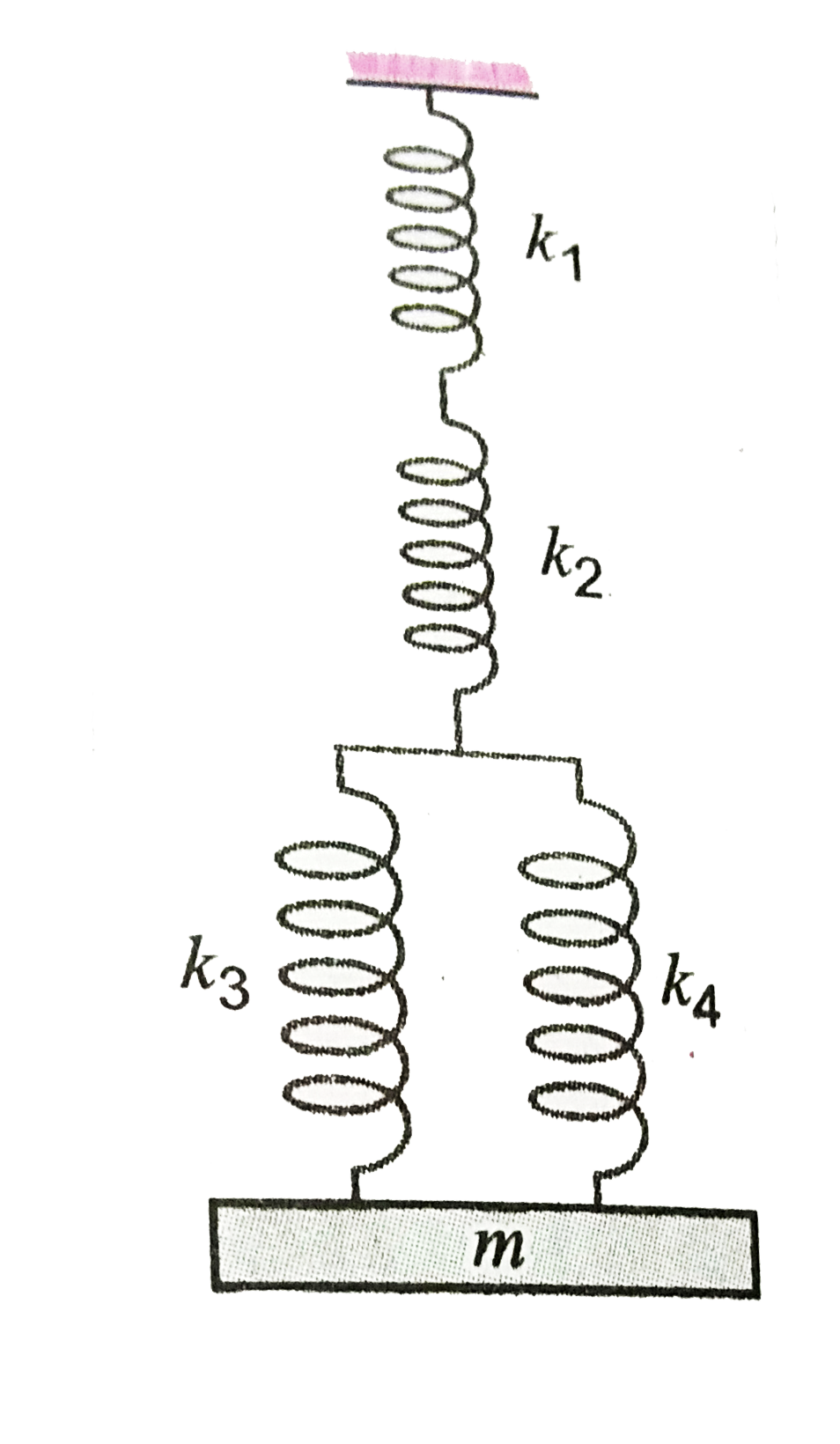
A system of springs with their spring constants are as shown in figure. What is the frequency of oscillations of the mass m ?
View SolutionTwo identical springs, each of spring factor k, may be connected in the following ways. Deduce the spring factor of the oscillation of the body in each case.
View SolutionTwo springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is

View SolutionTwo spring of force constants K and 2K are connected a mass m below The frequency of oscillation the mass is
View SolutionInfinite springs with force constants k,2k,4k,8k,….. respectively are connected in series to which mass 'm' is attched. The frequency of small oscillations is……..
View Solution
