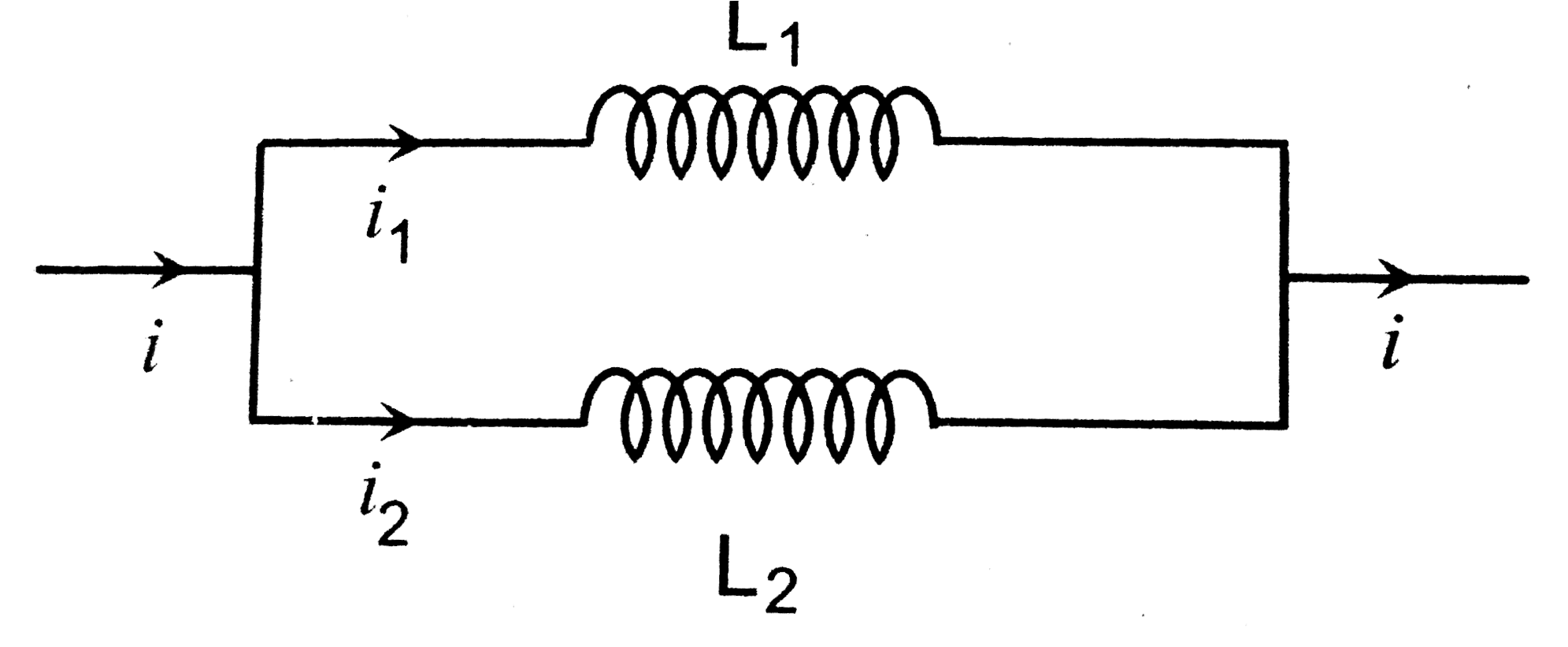
Two inductors L1 and L2 are connected in parallel and a time varying current flows as shown.
the ratio of current i1/i2
L2L1
L1L2
L22(L1+L2)2
L21(L1+L2)2
The correct Answer is:A
As the inductors are in parallel, induced emf across the two inductors is the same, i.e,
e1=e2
L1(di1dt)=L2(di2dt)
On integrating both sides, we get
L1∫di1dt=L2∫di2dt
L1i1=L2i2
⇒i1i2=L2L1
Topper's Solved these Questions
Similar Questions
In the circuit shown in figure ,find the ratio of currents i1/i2.

View SolutionInductors in parallel. Two inductors L1 and L2 are connected in parallel and separated by a large distance so that the magnetic field of one cannot affect the other. (a) Show that the equivalent inductance is given by
1Leq=1L1=1L2
(Hint: Review the derivations for resistors in parallel and capacitors in parallel. Which is similar here?) (b) What is the generalization of (a) for N inductors in parallel?
View Solution
Knowledge Check
Two inductors L1 and L2 are connected in parallel and a time varying current flows as shown.
the ratio of current i1/i2
 AL2L1BL1L2CL22(L1+L2)2DL21(L1+L2)2
AL2L1BL1L2CL22(L1+L2)2DL21(L1+L2)2In the circuit as shown in figure, the ratio of current i1/i2 is
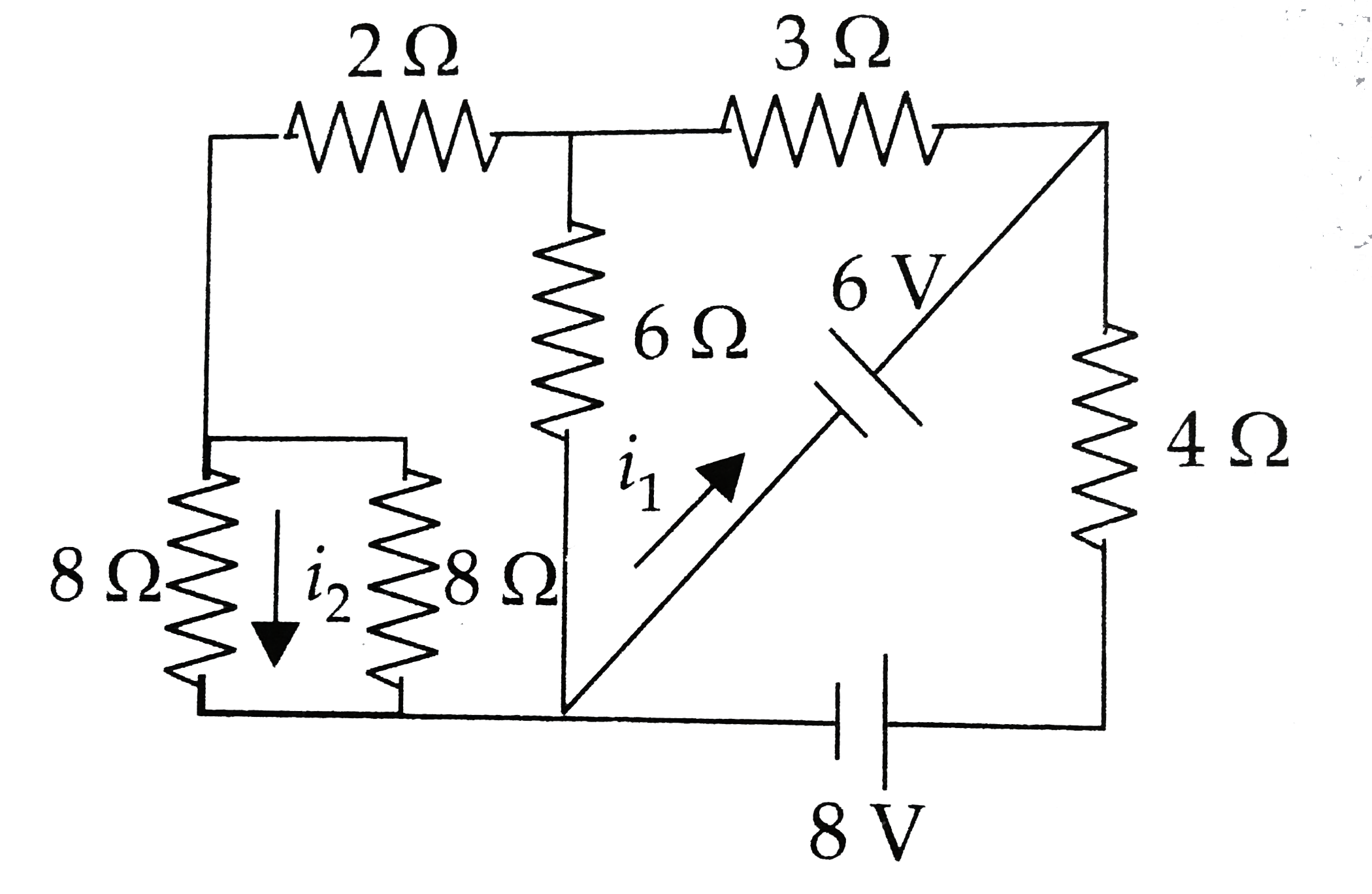 A4/3B1/2C2Dnone of these
A4/3B1/2C2Dnone of theseIn the circuit shown, the currents i1 and i2 are
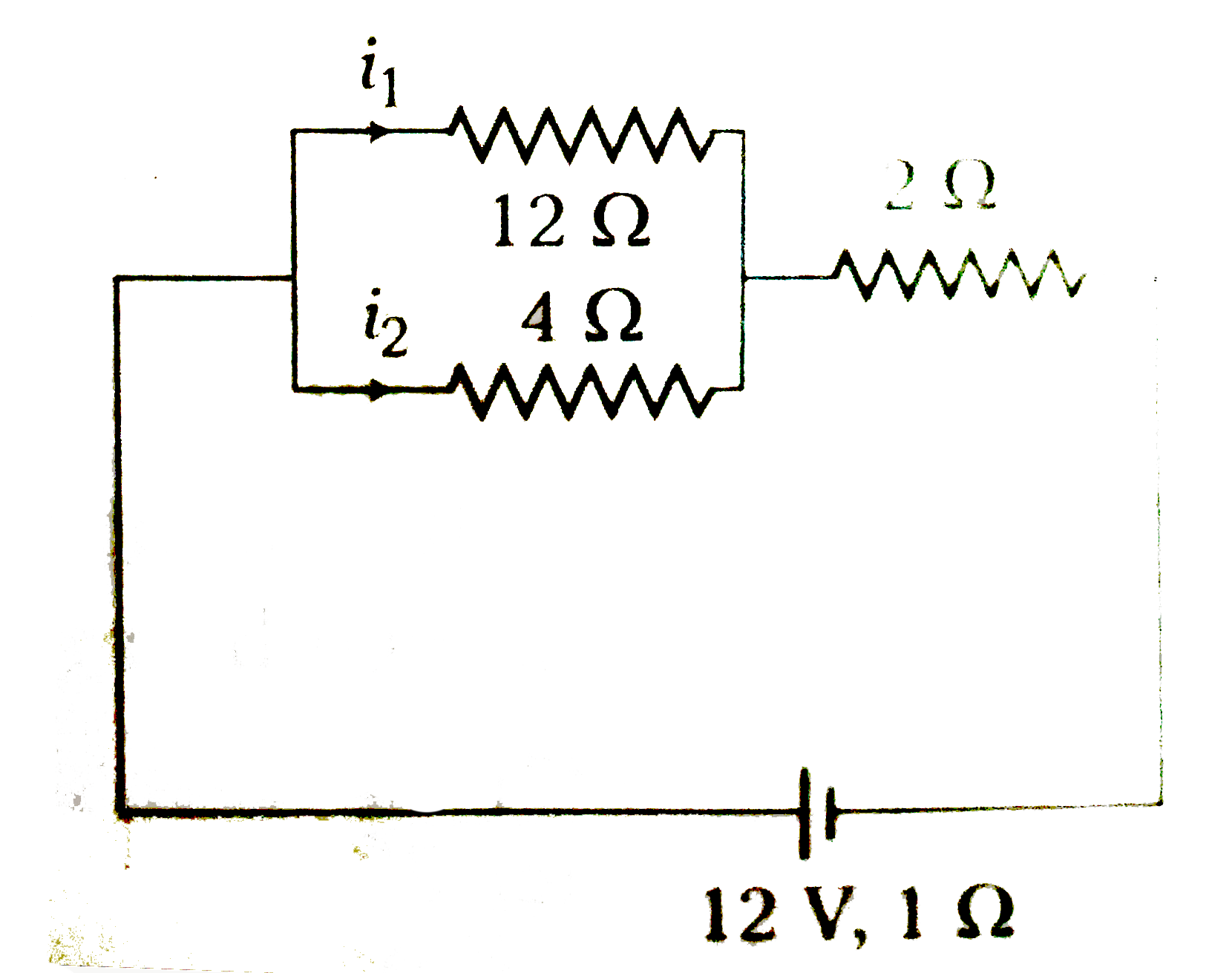 Ai1=1.5A,i2=0.5ABi1=0.5A,i2=1.5ACi1=1A.i2=3ADi1=3A,i2=1A
Ai1=1.5A,i2=0.5ABi1=0.5A,i2=1.5ACi1=1A.i2=3ADi1=3A,i2=1A
Two coils of self inductance L1 and L2 are connected in parallel and then connected to a call of emf ε and internal resistance - R. Find the steady state current in the coils.
View SolutionTwo inductors L1 and L2 are at a sufficient distance apart. Equivalent inductance when they are connected (i) in series (ii) in parallel are
View SolutionIf I1,I2,I3 and I4 are the respective r.m.s. values of the time varying currents as shown in the four cases I, II, III and IV. Then identify the correct relations.

View SolutionIn the circuit shown, the value of currents I1,I2andI3 are
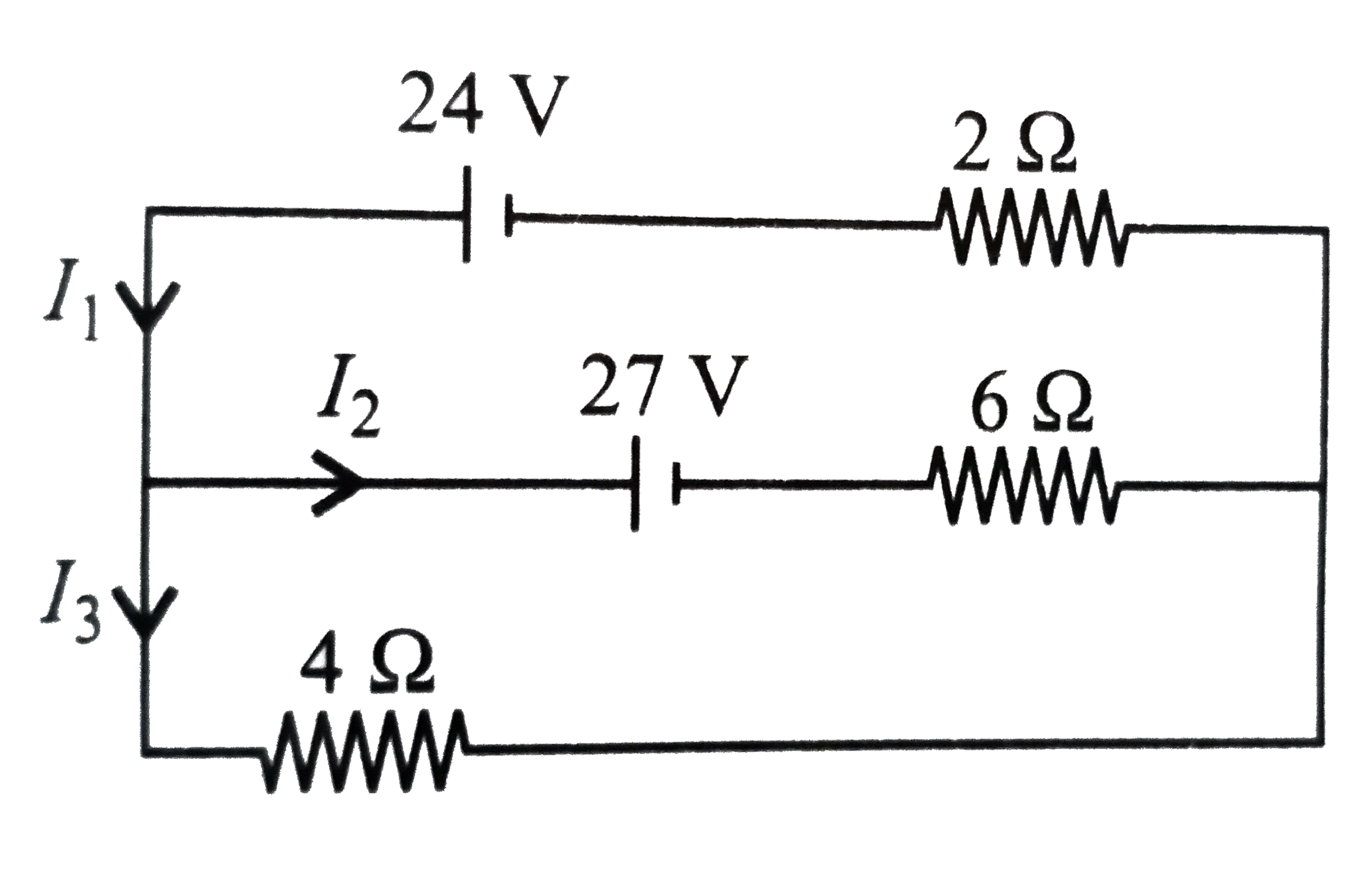
View SolutionTwo wires of different materials of resistivity p1andp2 , length l1andl2, and area of cross-section A1andA2 respectively are connected in parallel. The ratio of current density in the two wires,j1j2 , is given by:
View Solution
