Two infinitely long linear conductors are arranged perpendicular to each other and are in mutually perpendicular planes as shown in Fig. If I1=2A along the y-axis, I2=3A, along -ve z-axis and AP=AB=1cm, the value of magnetic field strength →B at P is

(3×10−5T)ˆj+(−4×10−5T)ˆk
(3×10−5T)ˆj+(4×10−5T)ˆk
(4×10−5T)ˆj+(−4×10−5T)ˆk
(−3×10−5T)ˆj+(4×10−5T)ˆk
The correct Answer is:B
(b) Magnetic field strength at P due to I1
→B1=μ0I2π(AP)ˆk=4π×10−7×22π×1×10−2ˆk=(4×10−5T)ˆk
Magnetic field strength at P due the I2
→B2=μ0I22π(BP)ˆj=4π×10−7×32π×2×10−2ˆj=(3×10−5T)ˆj
Hence, →B=(3×10−5T)ˆj+(4×10−5T)ˆk
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICSChapter:SOURCES OF MAGNETIC FIELDExercise:Exercise (multiple Currect )
Explore 5 Videos
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICSChapter:SOURCES OF MAGNETIC FIELDExercise:Exercise (assertion-reasioning )
Explore 2 Videos
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICSChapter:SOURCES OF MAGNETIC FIELDExercise:Exercise (subjective )
Explore 10 Videos
- SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSBook:CENGAGE PHYSICSChapter:SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSExercise:QUESTION BANK
Explore 12 Videos
- THERMAL PROPERTIES OF MATTERBook:CENGAGE PHYSICSChapter:THERMAL PROPERTIES OF MATTERExercise:Question Bank
Explore 40 Videos
Similar Questions
A circular loop of wire of radius R is bent about its diameter along two mutually perpendicular planes as shown in Fig. If the loop carries a current I, then determine its magnetic moment.
View SolutionTwo insulating infinite long conductors carrying currents I1(=2A) and I2(=4A) lie mutually perpendicular to each other in the same plane, as shown in figure. Find the magnetic field at the point P(a,b), where a=4cm, , b=3cm.
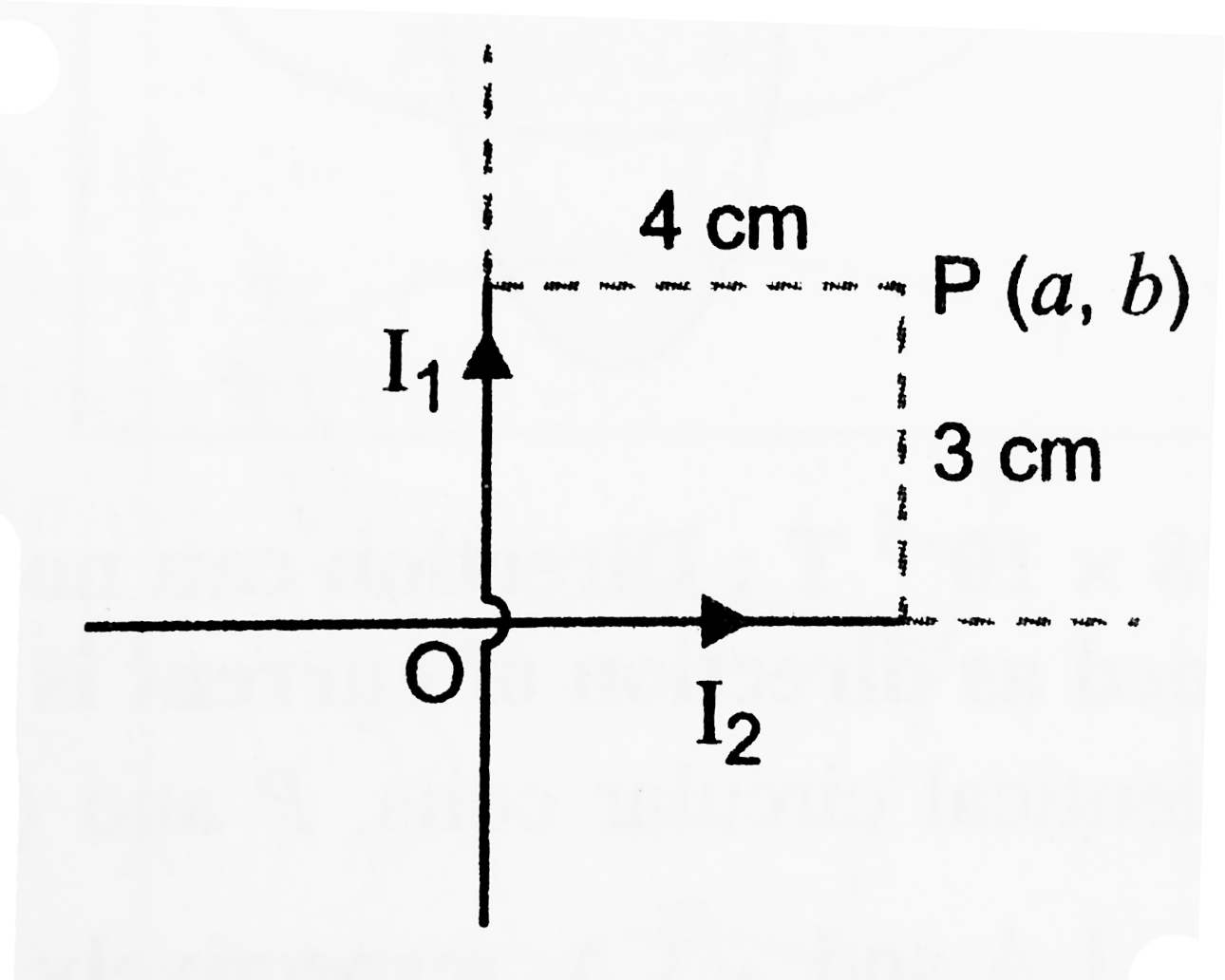
View Solution
Knowledge Check
Three infinitely long thin conductors are joined at the origin of coordinates and lie along the x-y- and z-axes. A current i flowing along the conductor lying along the x-axis divides equally into the othere two at the origin. The magnetic field at the point (0,-a,0) has magnitude
Aμ0i4πaB3μ0i4√2πaC√5μ0i8πaD√3μ0i2πaEquation of plane passing through (2,1,0), and perpendicular to the unit vector ˆk along the Z-axis is
Ax=2By=1Cx+y=3Dz=0Three long wires, each carrying current i are placed as shown. The middle wire is along Y-axis. The locus of point on the X-axis where magnetic field is zero is
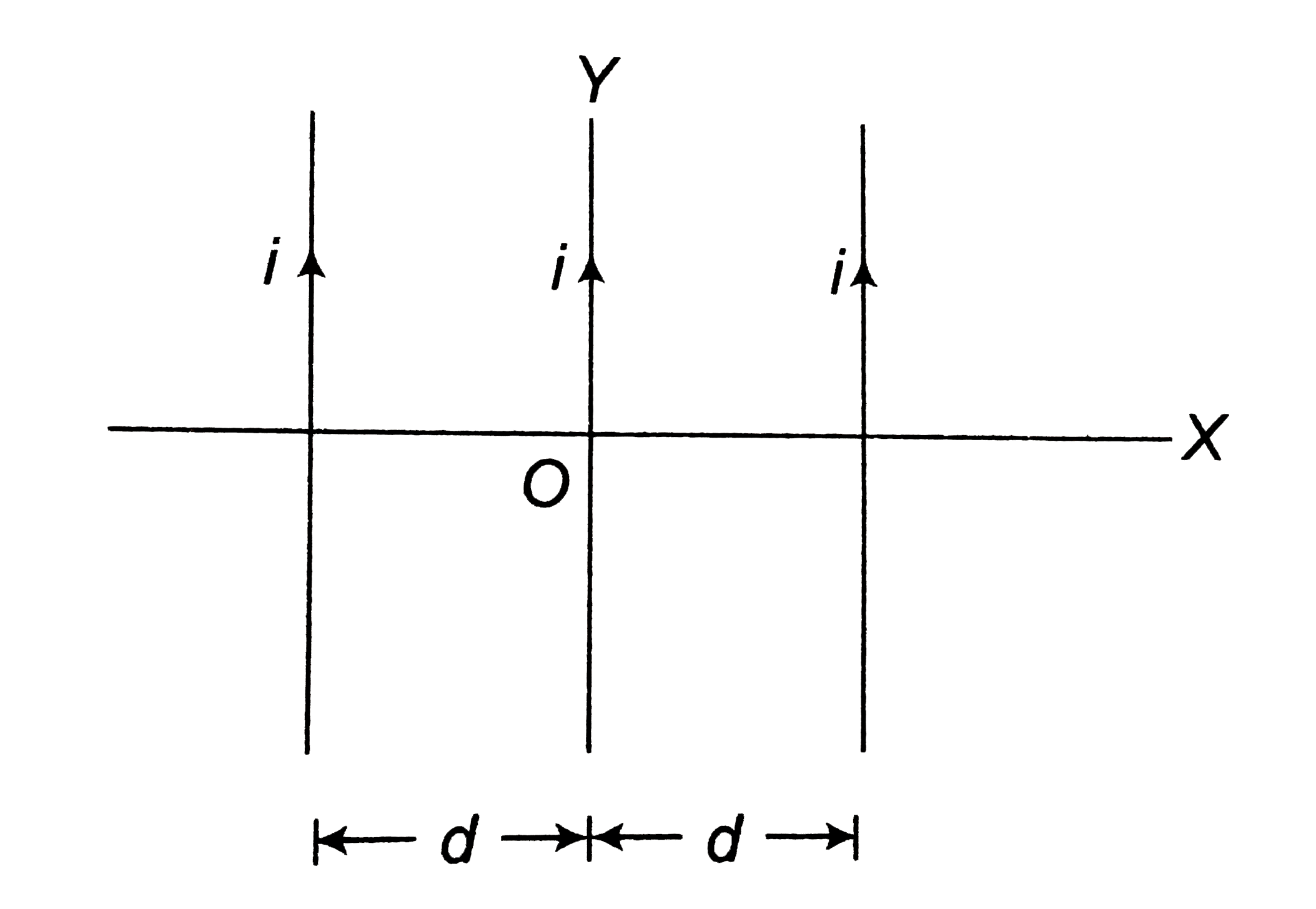 Ax=0Bx=d√3Cx=−d√3Dall
Ax=0Bx=d√3Cx=−d√3Dall
Calculate the magnitude of the magnetic field at point P as shown in Fig, in terms of R,I1andI2.

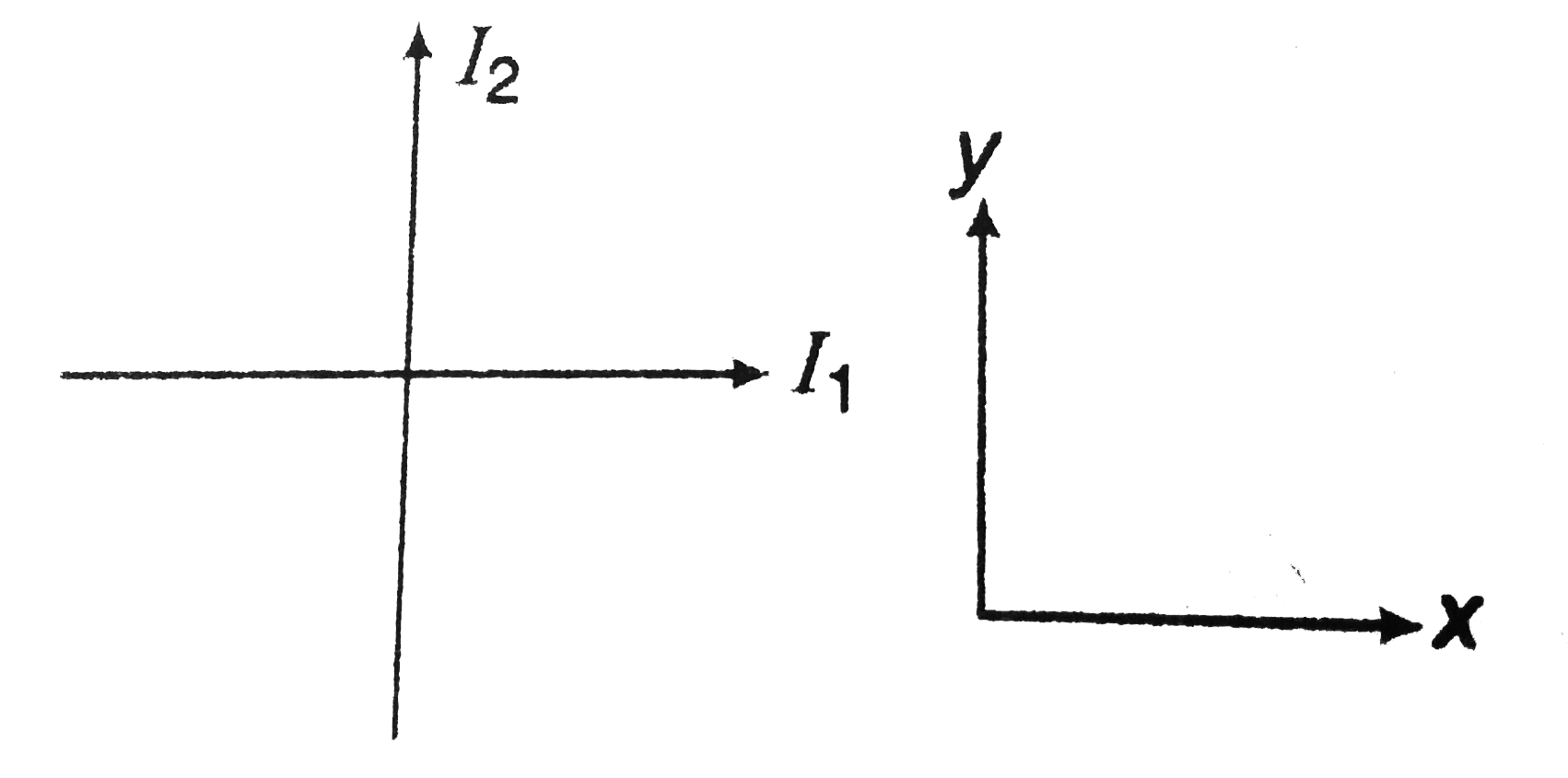
View SolutionElectric currents I1 and I2 are flowing in two mutually perpendicular conductors as shown in figure. Find the equation of locus of zero magnetic field points.

View SolutionTwo long mutually perpendicular conductors carrying currents I1 and I2 lie in one plane, Find the locus of points at which the magnetic induction is zero.
View SolutionThree infinitely long thein wires, each carrying curren i int eh same diecrtion, are the dxy plane of a gravilty free space. The central wire is along the y-axis while the other two are along x=±d
i find the locus of the points for which the magnetic field B is zero.
ii If the central wire is displaced along the z-direction by a smal amount and released, show that it will execute simple harmonic motion. If the linear mass density of the wires is λ, find the frequency of oscillation.
View SolutionTwo infinitely long wires each carrying current I along the same direction are made into the geometry as shown in the figure. The magnetic field at the point P is

View Solution