Two long current carrying wires A and B separated by 20 cm are carrying currents of 10 A and 20 A respectively in the opposite directions. Find the magnitude and direction of magnitic field at a point 10 em from both the wires.
To solve the problem of finding the magnitude and direction of the magnetic field at a point 10 cm from both wires A and B, we will follow these steps:
Step 1: Understand the Setup
We have two long current-carrying wires, A and B, separated by a distance of 20 cm. Wire A carries a current of 10 A, and wire B carries a current of 20 A in opposite directions. We need to find the magnetic field at a point that is 10 cm away from both wires.
Step 2: Use the Formula for Magnetic Field
The magnetic field (B) at a distance (D) from a long straight wire carrying current (I) is given by the formula:
B=μ04π⋅2ID
where μ0 (the permeability of free space) is approximately 4π×10−7T m/A.
Step 3: Calculate the Magnetic Field due to Wire A (B1)
For wire A:
- Current I1=10A
- Distance from point P to wire A D1=10cm=0.1m
Using the formula:
B1=μ04π⋅2I1D1=4π×10−74π⋅2×100.1
B1=10−7⋅200=2×10−5T
Step 4: Calculate the Magnetic Field due to Wire B (B2)
For wire B:
- Current I2=20A
- Distance from point P to wire B D2=10cm=0.1m
Using the formula:
B2=μ04π⋅2I2D2=4π×10−74π⋅2×200.1
B2=10−7⋅400=4×10−5T
Step 5: Determine the Direction of the Magnetic Fields
Using the right-hand thumb rule:
- For wire A (10 A), the magnetic field at point P (between the two wires) is directed downward.
- For wire B (20 A), the magnetic field at point P is also directed downward.
Step 6: Calculate the Net Magnetic Field
Since both magnetic fields are in the same direction (downward), we can add them:
Bnet=B1+B2=2×10−5+4×10−5=6×10−5T
Step 7: State the Final Answer
The magnitude of the magnetic field at the point 10 cm from both wires is:
Bnet=6×10−5T
The direction of the magnetic field is downward.
---
We have two long current-carrying wires, A and B, separated by a distance of 20 cm. Wire A carries a current of 10 A, and wire B carries a current of 20 A in opposite directions. We need to find the magnetic field at a point that is 10 cm away from both wires.
The magnetic field (B) at a distance (D) from a long straight wire carrying current (I) is given by the formula:
B=μ04π⋅2ID
where μ0 (the permeability of free space) is approximately 4π×10−7T m/A.
For wire A:
- Current I1=10A
- Distance from point P to wire A D1=10cm=0.1m
B1=μ04π⋅2I1D1=4π×10−74π⋅2×100.1
B1=10−7⋅200=2×10−5T
For wire B:
- Current I2=20A
- Distance from point P to wire B D2=10cm=0.1m
B2=μ04π⋅2I2D2=4π×10−74π⋅2×200.1
B2=10−7⋅400=4×10−5T
Using the right-hand thumb rule:
- For wire A (10 A), the magnetic field at point P (between the two wires) is directed downward.
- For wire B (20 A), the magnetic field at point P is also directed downward.
Since both magnetic fields are in the same direction (downward), we can add them:
Bnet=B1+B2=2×10−5+4×10−5=6×10−5T
The magnitude of the magnetic field at the point 10 cm from both wires is:
Bnet=6×10−5T
The direction of the magnetic field is downward.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBook:MODERN PUBLICATIONChapter:MOVING CHARGES AND MAGNETISMExercise:PRACTICE PROBLEMS
Explore 59 Videos
- MOVING CHARGES AND MAGNETISMBook:MODERN PUBLICATIONChapter:MOVING CHARGES AND MAGNETISMExercise:Conceptual Questions
Explore 29 Videos
- MAGNETISM AND MATTERBook:MODERN PUBLICATIONChapter:MAGNETISM AND MATTERExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 16 Videos
- NUCLEIBook:MODERN PUBLICATIONChapter:NUCLEIExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 15 Videos
Similar Questions
Two long parallel straight wires X and Y separated by a distance 5cm in air carry currents of 10A and 5A respectively in opposite directions. Calculate the magnitude and direction of force on a 20cm length of the wire Y. Figure

View SolutionFind the magnitude and direction of magnetic field at point P due to the current carrying wire as shown in

View Solution
Knowledge Check
Two long parallel wires are 30 cm apart carrying currents 10 A and 15 A respectively in the same direction. The force acting over a length of 5 m of the wires is
A5×10−4N, (attraction)B1×10−4N, (attraction)C5×10−4N, (repulsion)D1×10−4N, (repulsion)Two long parallel current carrying conductors 30 cm apart having current each of 10 A in opposite direction, then value of magentic field at a point of 10 cm between them, from any of the wire.
A1×10−5TB6×10−5TC1.5×10−5TD3×10−5TTwo long straight wires are arranged parallel to each other and are kept 10 cm apart in vacuum. They carry currents of 5A and 10A respectively in the same direction. What is the magnetic force on a lergth of 20 cm of either wire ?
A10−5NB2×10−5MC3×10−5ND4×10−5N
Figure shows two parallel wires separated by a distance of 4.0 cm and carrying equal currents of 10A along opposite directions. Find the magnitude of the magnetic field B at the points A1,A2,A3andA4.

View SolutionThere are two parallel current carrying wires X and Y as shown in figure. Find the magnitude and direction of the magnetic field at points, P, Q and R.
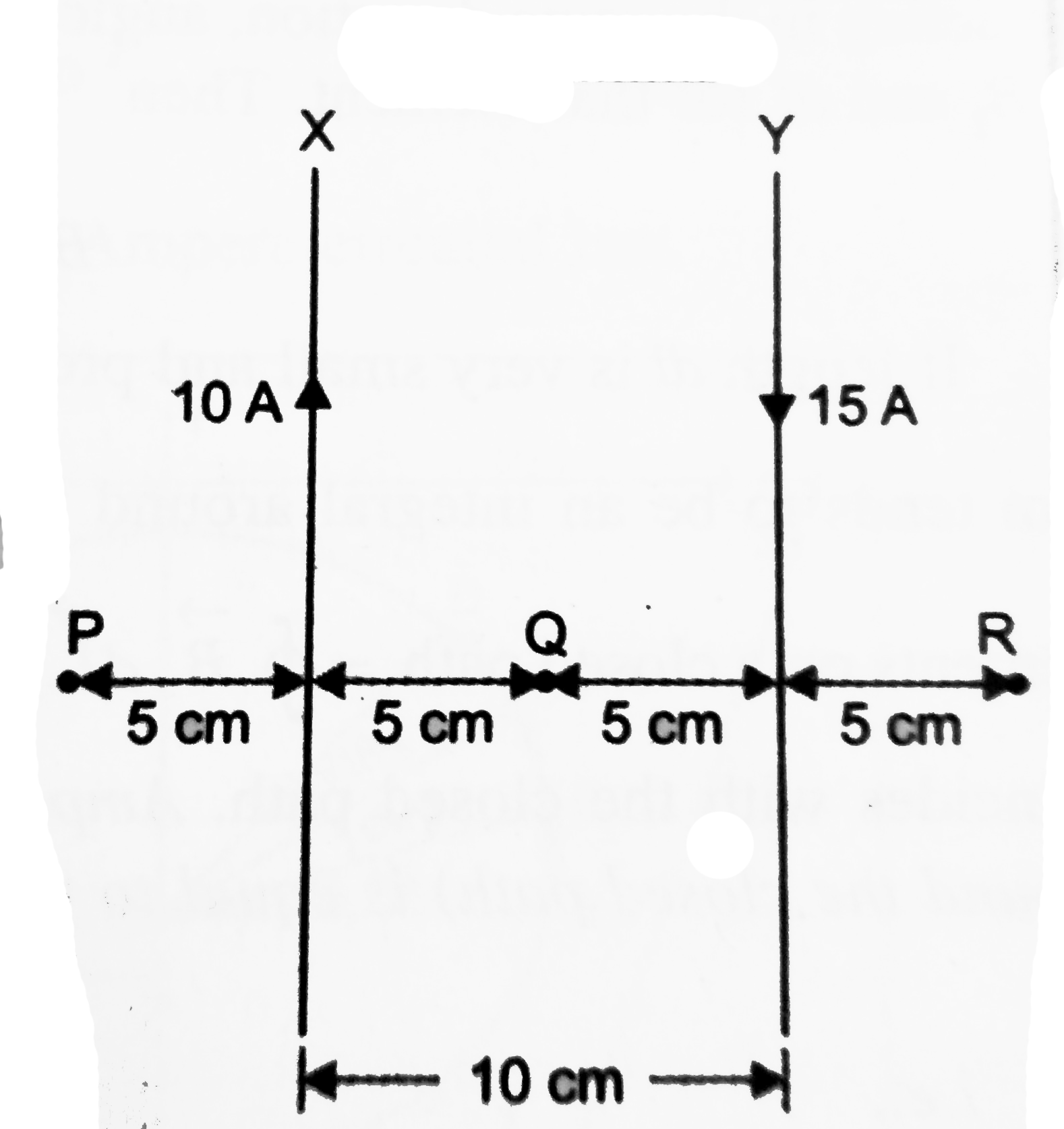
View SolutionFig shows two current-carrying wires 1 and 2. Find the magnitudes and directions of the magnetic field at points P,Q and R.

View SolutionTwo parallel wires carry equal currents of 10A along the same direction and are separated by a distance of 2.0 cm. Find the magnetic field at a point which is 2.0 cm away from each of these wires.
View SolutionTwo long parallel wires separated by 0.1m carry currents of 1A and 2A respectively in opposite directions. A third current carrying wire parallel to both of them is placed in the same plane such that it feels no net magnetic force. It is placed at a distance of
View Solution