Two long, parallel straight wires are separated by a distance of cm and carry current of 10 A and 8 A.
Find the magnitude of the attractive force exerted on 1 m length of one wire by the other wire.
To find the magnitude of the attractive force exerted on 1 m length of one wire by the other wire, we can follow these steps:
1. Identify the Given Data:
- Distance between the wires, D=0.2cm=0.2×10−2m=0.002m
- Current in the first wire, I1=10A
- Current in the second wire, I2=8A
- Length of the wire, L=1m
2. Use the Formula for the Magnetic Force Between Two Parallel Wires:
The formula for the force per unit length between two parallel wires carrying currents I1 and I2 separated by a distance D is given by:
F=μ0I1I22πDL
where μ0 is the permeability of free space, approximately μ0=4π×10−7T m/A.
3. Substitute the Values into the Formula:
F=(4π×10−7)×(10)×(8)2π×(0.002)×1
4. Simplify the Expression:
- The π terms cancel out:
F=(4×10−7)×(10)×(8)2×(0.002)
- Calculate the denominator:
2×0.002=0.004
- Now substitute:
F=(4×10−7)×800.004
5. Calculate the Force:
- First, calculate 4×80=320:
F=320×10−70.004
- Convert 0.004 to scientific notation:
0.004=4×10−3
- Now, substitute this back:
F=320×10−74×10−3=80×10−4=8×10−3N
6. Final Result:
The magnitude of the attractive force exerted on 1 m length of one wire by the other wire is:
F=8×10−3N
- Distance between the wires, D=0.2cm=0.2×10−2m=0.002m
- Current in the first wire, I1=10A
- Current in the second wire, I2=8A
- Length of the wire, L=1m
The formula for the force per unit length between two parallel wires carrying currents I1 and I2 separated by a distance D is given by:
F=μ0I1I22πDL
where μ0 is the permeability of free space, approximately μ0=4π×10−7T m/A.
F=(4π×10−7)×(10)×(8)2π×(0.002)×1
- The π terms cancel out:
F=(4×10−7)×(10)×(8)2×(0.002)
- Calculate the denominator:
2×0.002=0.004
- Now substitute:
F=(4×10−7)×800.004
- First, calculate 4×80=320:
F=320×10−70.004
- Convert 0.004 to scientific notation:
0.004=4×10−3
- Now, substitute this back:
F=320×10−74×10−3=80×10−4=8×10−3N
The magnitude of the attractive force exerted on 1 m length of one wire by the other wire is:
F=8×10−3N
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - COMPETITION FILE (A. MULTIPLE CHOICE QUESTIONS)38videos
MOVING CHARGES AND MAGNETISM
- BOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - COMPETITION FILE (B. MULTIPLE CHOICE QUESTIONS)79videos
MOVING CHARGES AND MAGNETISM
- BOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Revision Exercises (Long Answer Questions )12videos
MOVING CHARGES AND MAGNETISM
- BOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION16videos
MAGNETISM AND MATTER
- BOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION15videos
NUCLEI
Similar Questions
Two long parallel straight wires X and Y separated by a distance 5cm in air carry currents of 10A and 5A respectively in opposite directions. Calculate the magnitude and direction of force on a 20cm length of the wire Y. Figure
 View Solution
View SolutionTwo long, parallel wires are separated by a distance of 0.400m (as shown in Fig.) The current I1andI2 have the direction shown.
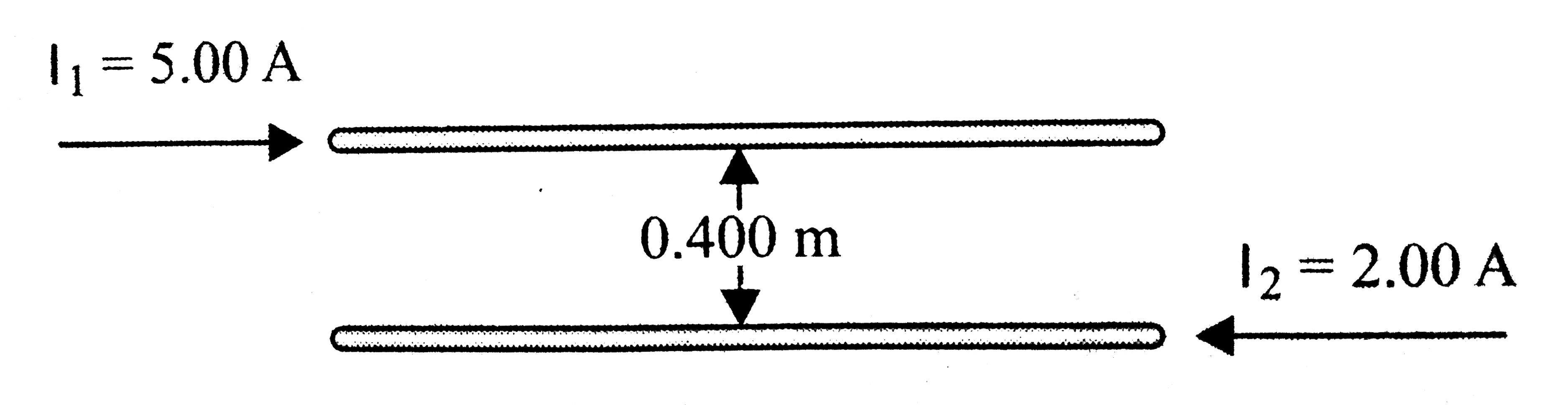
(a) Calculate the magnitude of the force exerted by each wire on a 1.20m length of the other. Is the force attractive or repulsive ?
(b) Each current is doubled, so that I1 becomes 10.0A and I2 becomes 4.00A. Now, what is the magnitude of the force that each wire exerts on a 1.20m length of the other?View Solution
Knowledge Check
- Question 1 - Select One
Two thin, long, parallel wires, separated by a distance 'd' carry a current of 'i' A in the same direction. They will
Arepel each other with a force of μ0i2/(2πd)Battract each other with a force of μ0i2/(2πd)Crepel each other with a force of μ0i2/(2πd2)Dattract each other with a force of μ0i2/(2πd2) - Question 2 - Select One
Two thin long paralel wires separated by a distance b are carrying a current 1 A each. The magnitude of the force per unit length exerted by one wire on the other is
Aμ0I2b2Bμ0I22πbCμ0I2πbDμ0I2πb2 - Question 3 - Select One
Two thin long parallel wires separated by a distance b are carrying a current I A each. The magnitude of the force per unit length exerted by one wire on the other is
Aμ0i2b2Bμ0i2πb2Cμ0i2πbDμ0i22πb
Two infinite, parallel wires are a distance 10 cm apart and carry equal current 20 A in the same direction. The magnetic force on a 1 cm long segment of one wire due to the other wire is ___________ ×10−6N. (Permeabilityi of vacuum μ0=4π×10−7N/A2)
View SolutionTwo thin long parallel wires seperated by a distance 'b' are carrying a current ' I' amp each . The magnitude of the force3 per unit length exerted by one wire on the other is
View SolutionTwo thin and parallel wires are placed at a distance b and I current is flowing through each of the wires. The magnitude of the force exerted on the unit length of wire due to another wire will be :
View SolutionTwo thin and parallel wires are placed at a distance b and I current is flowing through each of the wires. The magnitude of the force exerted on the unit length of wire due to another wire will be :
View SolutionTwo thin long parallel wires separated by a distance 'd' are carrying same current I. The magnitude of the force per unit length exerted by one wire on the other is
View Solution

