Two masses 8 kg 4 kg are suspended together by a massless spring of spring constant 1000Nm−1 . When the masses are in equilibrium 8 kg is removed without disturbing the system. The amplitude of oscillation is
0.5 m
0.08 m
0.4 m
0.04 m
The correct Answer is:B
To solve the problem step by step, we will follow these instructions:
Step 1: Understand the System
We have two masses, 8 kg and 4 kg, suspended together by a massless spring with a spring constant k=1000N/m. When both masses are attached, they will stretch the spring to a certain equilibrium position.
Step 2: Calculate the Total Mass
The total mass when both weights are attached is:
mtotal=8kg+4kg=12kg
Step 3: Find the Equilibrium Position
Using Hooke's Law, the extension x of the spring at equilibrium can be calculated using the formula:
kx=mg
where m is the total mass and g is the acceleration due to gravity (approximately 10m/s2).
Substituting the values:
1000x=12kg×10m/s2
1000x=120N
x=1201000=0.12m
Step 4: Remove the 8 kg Mass
Now, we remove the 8 kg mass from the system. The remaining mass is 4 kg.
Step 5: Calculate the New Equilibrium Position
Now we need to find the new equilibrium position with only the 4 kg mass:
kx1=mg
Substituting the values:
1000x1=4kg×10m/s2
1000x1=40N
x1=401000=0.04m
Step 6: Calculate the Amplitude of Oscillation
The amplitude of oscillation is the difference between the initial maximum displacement (with both masses) and the new maximum displacement (with only the 4 kg mass):
Amplitude=x−x1=0.12m−0.04m=0.08m
Final Answer
The amplitude of oscillation after removing the 8 kg mass is:
Amplitude=0.08m
We have two masses, 8 kg and 4 kg, suspended together by a massless spring with a spring constant k=1000N/m. When both masses are attached, they will stretch the spring to a certain equilibrium position.
The total mass when both weights are attached is:
mtotal=8kg+4kg=12kg
Using Hooke's Law, the extension x of the spring at equilibrium can be calculated using the formula:
kx=mg
where m is the total mass and g is the acceleration due to gravity (approximately 10m/s2).
1000x=12kg×10m/s2
1000x=120N
x=1201000=0.12m
Now, we remove the 8 kg mass from the system. The remaining mass is 4 kg.
Now we need to find the new equilibrium position with only the 4 kg mass:
kx1=mg
Substituting the values:
1000x1=4kg×10m/s2
1000x1=40N
x1=401000=0.04m
The amplitude of oscillation is the difference between the initial maximum displacement (with both masses) and the new maximum displacement (with only the 4 kg mass):
Amplitude=x−x1=0.12m−0.04m=0.08m
The amplitude of oscillation after removing the 8 kg mass is:
Amplitude=0.08m
Similar Questions
Two masses m1 and m2 are suspended together by a massless spring of constant k. When the masses are in equilibrium, m1 is removed without disturbing the system. The amplitude of oscillations is

View SolutionTwo masses m1 and m2 are suspended together by a massless spring of constant K. When the masses are in equilibrium, m1 is removed without disturbing the system. Then the angular frequency of oscillation of m2 is -
View Solution
Knowledge Check
Two masses m1=1kgandm2=0.5kg are suspended together by a massless spring of spring constant 12.5Nm−1. When masses are in equilibrium m1 is removed without disturbing the system. New amplitude of oscillation will be
A30cmB50cmC80cmD60cmTwo masses m 1 and m 2 are suspended together by a massless spring of constant K . When the masses are in equilibrium, m 1 is removed without disturbing the system. The amplitude of oscillations is
 Am1gKBm2gKC(m1+m2)gKD(m1−m2)gK
Am1gKBm2gKC(m1+m2)gKD(m1−m2)gKTwo masses M and m are suspended together by massless spring of force constant -k. When the masses are in equilibrium, M is removed without disturbing the system. The amplitude of oscillations.
AMgkBmgkC(M+m)gkD(M−m)gk
Two mass m1 and m2 are suspended from a massless spring of force constant k. When the masses are in equilibrium, m1 is removed without disturbing the system. Find the angular frequency and amplitude of oscillations.
View SolutionTwo masses m1=1.0kgandm2=0.5kg are suspended together by a massless spring of force constant, k=12.5Nm−1. When they are in equillibrium position, m1 is gently removed. Calculate the angular frequency and the amplitude of oscillation of m2. Given g=10ms−2.
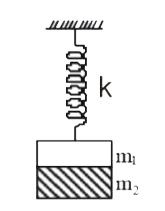
View SolutionTwo masses m1 and m2 are suspeded togther by a massless spring of spring constnat k (Fig). When the masses are in equilibrium, m1 is removed. Frequency and amplitude of oscillation of m2 are
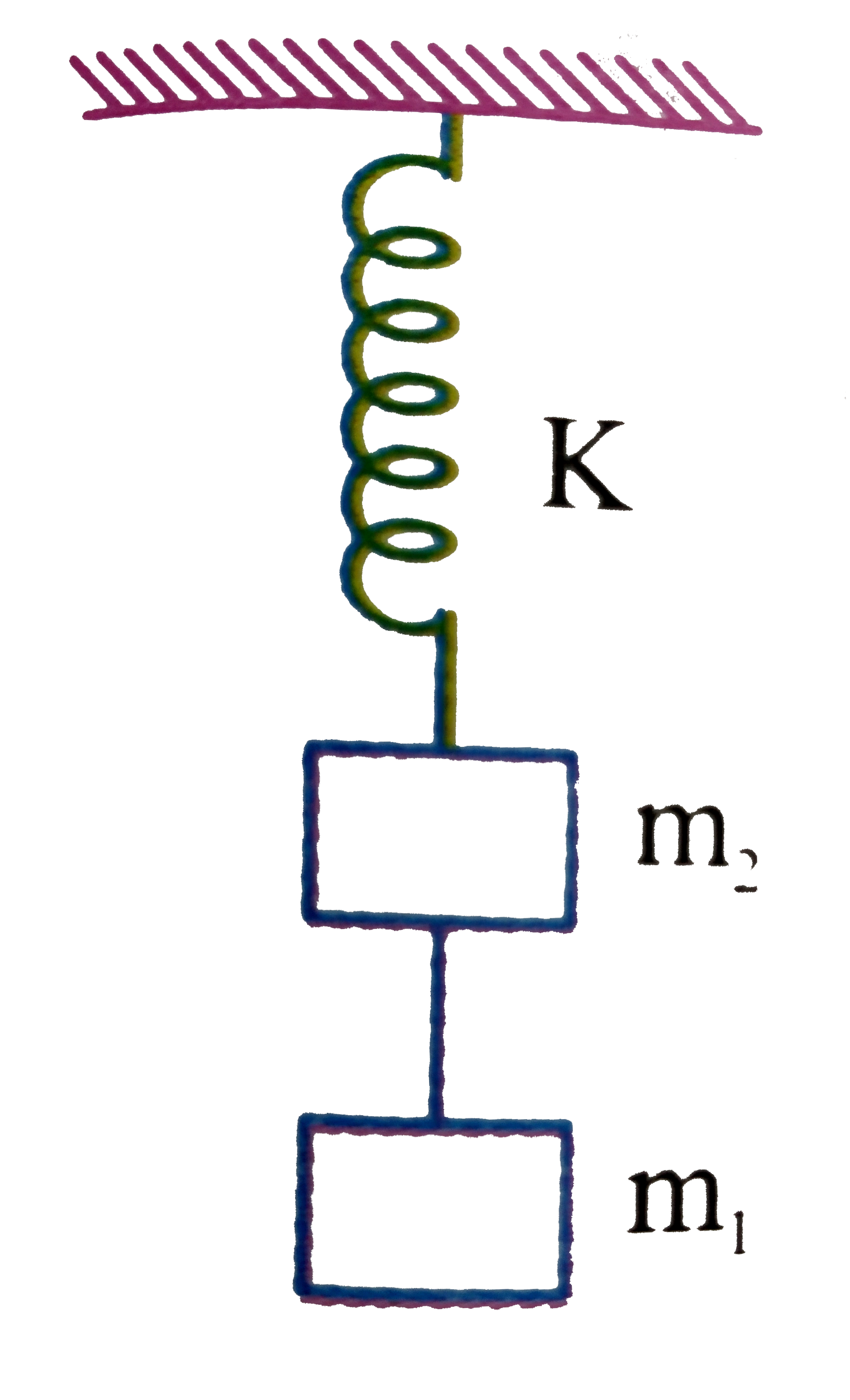
View SolutionTwo masses m1 and m2 are suspended w together by a light spring of spring constant k as shown in figure. When the system is in equilibrium, the mass m1 is removed without disturbing the system. As a result of this removal, mass m2 performs simple harmonic motion. For this situation mark the correct statement(s).
View SolutionTwo masses m1and m2 are suspended from a spring of spring constant 'k'. When the masses are in equilibrium, m1 is gently removed. The angular frequency and amplitude of oscillation of m2 will be respectively
View Solution
