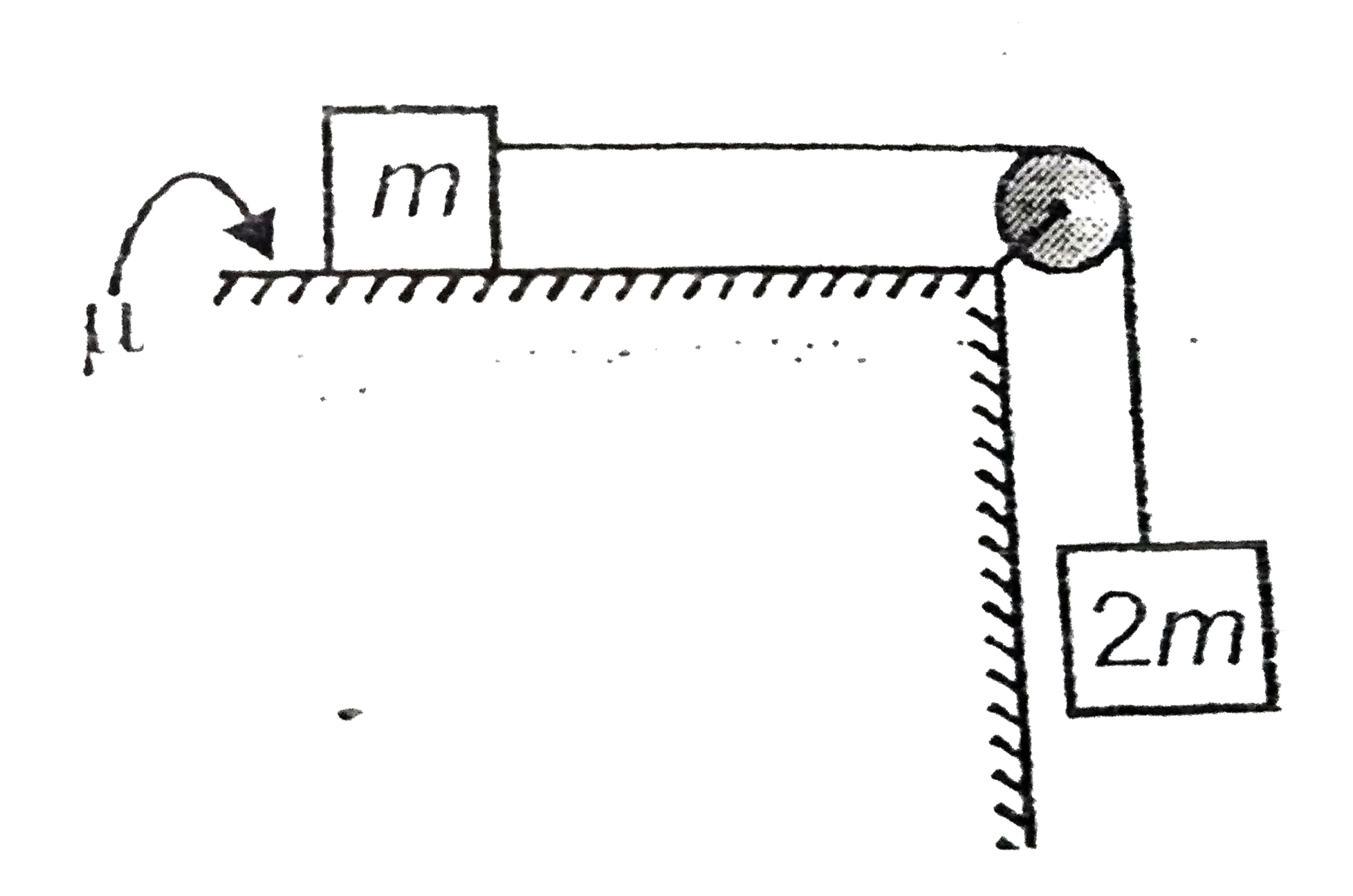
Two masses m1=10Kg and m2=5kg are connected by an ideal string as shown in the figure. The coefficient of friction between m1 and the surface is μ=0.2 Assuming that the system is released from rest calculate the velocity of blocks when m2hasdescendedby4m.(g=10 m//s^(2))
 .
.
The correct Answer is:D
vm1=vm2
dm1=hm2=4m
Using the equation,
Ei−Ef=
Work done against friction
0−[12×(10+5)(v2)−5×10×4]
=0.2×10×10×4
Solving we get,
v=4m/s
Similar Questions
Consider the system shown in the figure. Coefficient of friction between the block and table is μ=0.5. The system is released from rest. Find the work done by friction, when the speed of block is 10 m/s (m=1kg)
View SolutionTwo blocks of mass m1 and m2(m2>m1) are placed in contact with each other on an inclined plane as shown in figure . The coefficient of friction between m1 and surface is μ1 and between m2 and surface is μ2.



View Solution
Knowledge Check
Two blocks of masses M1=4 kg and M2=6kg are connected by a string of negligible mass passing over a frictionless pulley as shown in the figure below. The coefficient of friction between the block M1 and the horizontal surface is 0.4. when the system is released, the masses M1 and M2 start accelrating. What additional mass m should be placed over M1 so that the masses (M1+m) slide with a uniform speed?
 A12 kgB11 kgC10 kgDkg
A12 kgB11 kgC10 kgDkgTwo blocks A and B of mass 10 kg and 20 kg respectively are placed as shown in figure .Coefficient of friction between all the surface is 0.2 (g=10m/s2) Then,
 ATension in the string is 306 NBTension in the sr=tring is 132 NCaccelerration of block B is 2.6m/s2Dasseleration of block B is 4.7m/s2
ATension in the string is 306 NBTension in the sr=tring is 132 NCaccelerration of block B is 2.6m/s2Dasseleration of block B is 4.7m/s2Two moasses m1=5kgandm2=10kg, connected by an inextensible string over a frictionless pulley, are moving as shown in the figure. The coefficient of friction of horizontal surface is 0.15. The minimum weitght m that should be put on top of m2 to stop the motion is :-
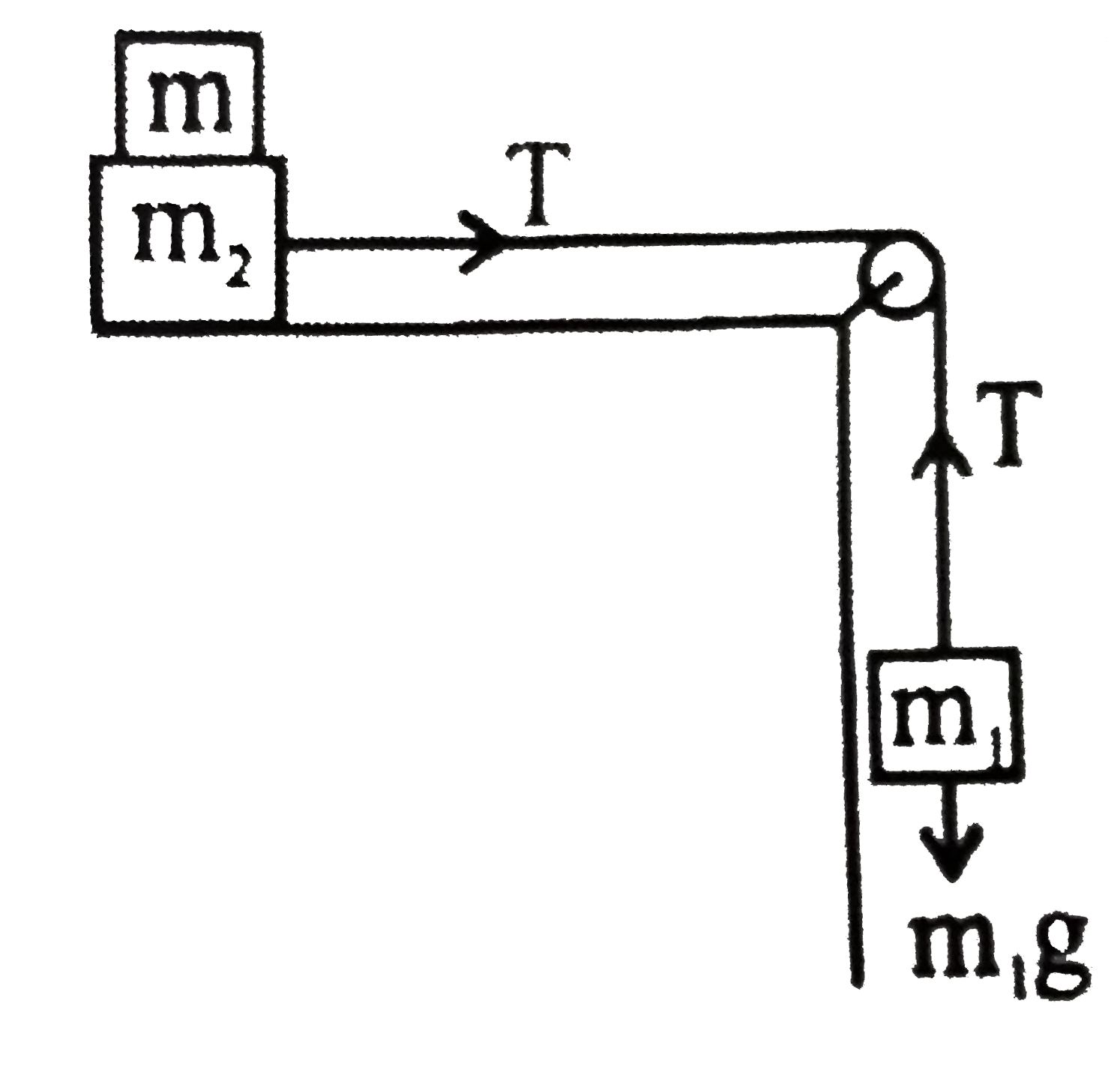 A27.3kgB43.3kgC10.3kgD18.3kg
A27.3kgB43.3kgC10.3kgD18.3kg
Two blocks A and B of mass 10 kg and 40 kg are connected by an ideal string as shown in the figure. Neglect the masses of the pulleys and effect of friction. (g = 10 m/s2) A B 45° Fixed 45°
View SolutionTwo blocks A and B of mass 10 kg and 40 kg are connected by an ideal string as shown in the figure. Neglect the masses of the pulleys and effect of friction. (g = 10 m/s2) А B 45° Fixed 45°
View SolutionTwo blocks of masses m1=1kgandm2=2kg are connected by a string and side down a plane inclined at an angle θ=45∘ with the horizontal. The coefficient of sliding friction between m1 and plane is μ1=0.4, and that between m2 and plane is μ2=0.2. Calculate the common acceleration of the two blocks and the tension in the string.

View SolutionTwo blocks of masses m1=10kg and m2=20kg are connected by a spring of stiffness k = 200 N/m. The coefficient of friction between the blocks and the fixed horizontal surface is μ=0.1. Find the minimum constant horizontal force F (in Newton) to be applied to m1 in order to slide the mass m2. (Take g=10m/s2)
View SolutionTwo block of masses m1 and m2 connected by a light spring rest on a horizontal plane. The coefficient of friction between the block and the surface is equal to μ. What minimum constant force has to be applied in the horizontal direction to the block of mass m1 in order to shift the other block?
View Solution
