Two masses m1andM2 are suspended together by a massless spring of constant k. When the masses are in equilibrium,m1is removed without disturbing the system. Then the angular frequency of oscillation ofm2 is
Let l1 and l2 be the extension produced by masses m1 and m2 respectively.
Then, (m1+m2)g=k(l1+l2)…(i)
After m1 is removed , m2g=kl2…(ii)
Eqs. (i) -(ii) gives m1g=kl1 or l1=m1gk
Now, angular frequency of m2,ω=2πT=2π√km2
Similar Questions
Two masses m1 and m2 are suspended together by a massless spring of constant k. When the masses are in equilibrium, m1 is removed without disturbing the system. The amplitude of oscillations is

View SolutionTwo mass m1 and m2 are suspended from a massless spring of force constant k. When the masses are in equilibrium, m1 is removed without disturbing the system. Find the angular frequency and amplitude of oscillations.
View Solution
Knowledge Check
Two masses m 1 and m 2 are suspended together by a massless spring of constant K . When the masses are in equilibrium, m 1 is removed without disturbing the system. The amplitude of oscillations is
 Am1gKBm2gKC(m1+m2)gKD(m1−m2)gK
Am1gKBm2gKC(m1+m2)gKD(m1−m2)gKTwo masses M and m are suspended together by massless spring of force constant -k. When the masses are in equilibrium, M is removed without disturbing the system. The amplitude of oscillations.
AMgkBmgkC(M+m)gkD(M−m)gkTwo masses m1=1kgandm2=0.5kg are suspended together by a massless spring of spring constant 12.5Nm−1. When masses are in equilibrium m1 is removed without disturbing the system. New amplitude of oscillation will be
A30cmB50cmC80cmD60cm
Two masses m1=1.0kgandm2=0.5kg are suspended together by a massless spring of force constant, k=12.5Nm−1. When they are in equillibrium position, m1 is gently removed. Calculate the angular frequency and the amplitude of oscillation of m2. Given g=10ms−2.
View SolutionTwo masses 8 kg 4 kg are suspended together by a massless spring of spring constant 1000Nm−1 . When the masses are in equilibrium 8 kg is removed without disturbing the system. The amplitude of oscillation is
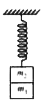
View SolutionTwo masses m1 and m2 are suspended w together by a light spring of spring constant k as shown in figure. When the system is in equilibrium, the mass m1 is removed without disturbing the system. As a result of this removal, mass m2 performs simple harmonic motion. For this situation mark the correct statement(s).
View SolutionTwo masses m1and m2 are suspended from a spring of spring constant 'k'. When the masses are in equilibrium, m1 is gently removed. The angular frequency and amplitude of oscillation of m2 will be respectively
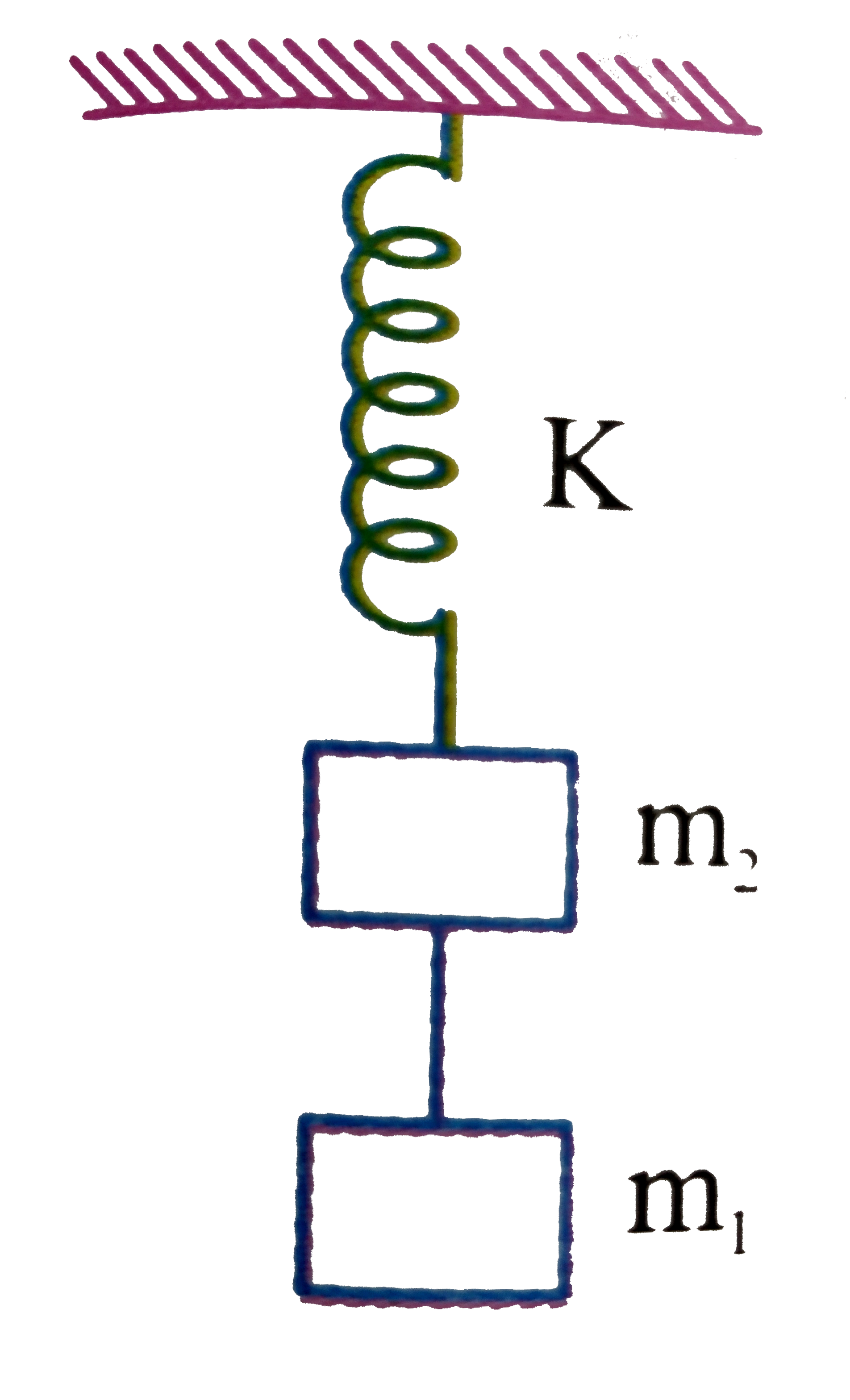
View SolutionTwo masses m1 and m2 are suspeded togther by a massless spring of spring constnat k (Fig). When the masses are in equilibrium, m1 is removed. Frequency and amplitude of oscillation of m2 are
View Solution
