Two masses of 500 gram and 600 grams are attached to the 10 cm and 80 cm marks respectively of a light metre scale. The moment of inertia of this system about an axis passing through the centre of the scale will be
The correct Answer is:A
To find the moment of inertia of the system about an axis passing through the center of the scale, we can follow these steps:
Step 1: Identify the masses and their positions
We have two masses:
- Mass m1=500g=0.5kg at the 10 cm mark (0.1 m)
- Mass m2=600g=0.6kg at the 80 cm mark (0.8 m)
Step 2: Determine the position of the axis
The axis of rotation is at the center of the meter scale, which is at the 50 cm mark (0.5 m).
Step 3: Calculate the distances from the axis
- For mass m1:
r1=0.5m−0.1m=0.4m
- For mass m2:
r2=0.8m−0.5m=0.3m
Step 4: Use the formula for moment of inertia
The moment of inertia I about the axis is given by the formula:
I=m1⋅r21+m2⋅r22
Step 5: Substitute the values into the formula
Substituting the values we have:
I=(0.5kg)⋅(0.4m)2+(0.6kg)⋅(0.3m)2
Calculating each term:
- First term:
0.5⋅(0.4)2=0.5⋅0.16=0.08kg m2
- Second term:
0.6⋅(0.3)2=0.6⋅0.09=0.054kg m2
Step 6: Add the contributions to find the total moment of inertia
I=0.08+0.054=0.134kg m2
Final Answer
The moment of inertia of the system about the axis passing through the center of the scale is:
0.134kg m2
---
We have two masses:
- Mass m1=500g=0.5kg at the 10 cm mark (0.1 m)
- Mass m2=600g=0.6kg at the 80 cm mark (0.8 m)
The axis of rotation is at the center of the meter scale, which is at the 50 cm mark (0.5 m).
- For mass m1:
r1=0.5m−0.1m=0.4m
- For mass m2:
r2=0.8m−0.5m=0.3m
The moment of inertia I about the axis is given by the formula:
I=m1⋅r21+m2⋅r22
Substituting the values we have:
I=(0.5kg)⋅(0.4m)2+(0.6kg)⋅(0.3m)2
- First term:
0.5⋅(0.4)2=0.5⋅0.16=0.08kg m2
0.6⋅(0.3)2=0.6⋅0.09=0.054kg m2
I=0.08+0.054=0.134kg m2
The moment of inertia of the system about the axis passing through the center of the scale is:
0.134kg m2
Topper's Solved these Questions
Similar Questions
Two masses of 3kg and 5kg are placed at 20cm and 70cm marks respectively on a light wooden meter scale. The M.I. of the system about an axis passing through 100 cm mark and perpendicular to the meter scale is
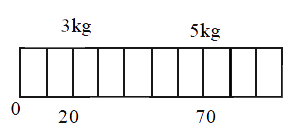
View SolutionTwo masses of 3kg and 5kg are placed at 20 cm and 70cm marks respectively on a light wooden meter scale. The M.I. of the system about an axis passign through 100cm mark and perpendicular to the meter scale is
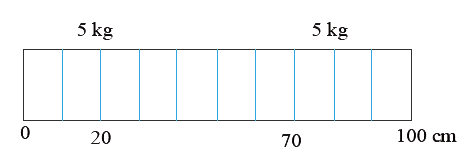
View Solution
Knowledge Check
If two masses of 200 g and 300 g are attached to the 20 cm and 70 cm marks on a light metre rod respectively, then the M.I. of the system about an axis passing through 50 cm mark will be
A0.15kgm2B0.03kgm2C0.3kgm2DzeroFive particles of mass 2 kg each are attached to the rim of a circular disc of radius 0.1 m and negligible mass. Moment of inertia of the system about the axis passing through the centre of the disc and perpendicular to its plane is
A1kg−m2B0.1kg−m2C2kg−m2D0.2kg−m2Five particles of mass 2 kg each are attached to the rim of a circular disc of radius 0.1 m and negligible mass. Moment of inertia of the system about the axis passing through the centre of the disc and perpendicular to its plane is
A1kgm2B0.1kgm2C2kgm2D0.2kgm2
Two masses of 3 kg and 5 kg are placed at 30 cm and 70 cm marks respectively on a light wooden meter scale, as shown in Fig. 8.51. what will the moment of inertia of the system about an axis through (i) 0 cm mark and (ii) 100 cm mark, and perpendicular to the meter scale?

View SolutionFive particles of mass 2 kg are attached to the rim of a circular disc of radius 0.1 m & negligible mass. Moment of inertia of the system about an axis passing through the centre of the disc & perpendicular to its plane is
View SolutionTwo masses m1 and m2 are attached to the ends of a light rod of length l.The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is (m1=m and m2 =2m)
View SolutionTwo masses m1andm2 are placed at a distance r from each other. Find out the moment of inertia of system about an axis passing through their centre of mass.
View SolutionTwo identical circular plates each of mass M and radius R are attached to each other with their planes ⊥r to each other. The moment of inertia of system about an axis passing through their centres and the point of contact is
View Solution
