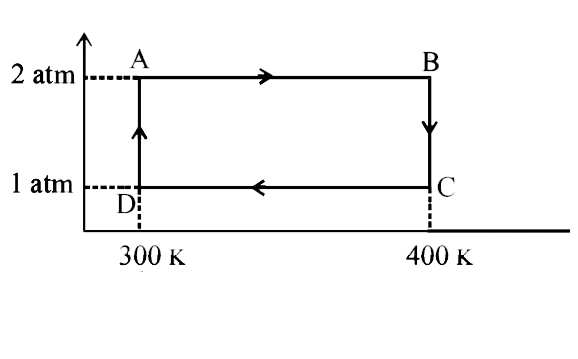
Two moles of helium gas undergo a cyclic process as shown in Fig. 19.2.14. Assuming the gas to be ideal, calculate the following quantitites in this process
(a) the net change in heat energy
(b) the net work done
(c) the net change in internal energy.
To solve the problem step by step, we will calculate the three quantities: the net change in heat energy (Q), the net work done (W), and the net change in internal energy (ΔU) for the cyclic process of 2 moles of helium gas.
Step 1: Calculate the Net Work Done (W)
1. Identify the Process: The process consists of three segments: AB, BC, and CA. We will calculate the work done in each segment.
2. Work Done in Segment AB (W_AB):
- For an isochoric process (constant volume), the work done is zero.
- Therefore, WAB=0.
3. Work Done in Segment BC (W_BC):
- For an isothermal expansion, the work done can be calculated using the formula:
WBC=NRTln(PBPC)
- Given values: N=2 moles, R=8.32J/(mol K), TB=400K, PB=2PC (assumed).
- Substitute values:
WBC=2×8.32×400×ln(2)≈2×8.32×400×0.693≈4.61kJ
4. Work Done in Segment CA (W_CA):
- For an isochoric process (constant volume), the work done is again zero.
- Therefore, WCA=0.
5. Total Work Done:
Wnet=WAB+WBC+WCA=0+4.61kJ+0=4.61kJ
Step 2: Calculate the Net Change in Heat Energy (Q)
1. Using the First Law of Thermodynamics:
Q=ΔU+W
- Since the process is cyclic, the net change in internal energy (ΔU) is zero.
- Therefore, Q=W.
2. Substituting the Work Done:
Q=4.61kJ
Step 3: Calculate the Net Change in Internal Energy (ΔU)
1. For a Cyclic Process:
- The net change in internal energy for a cyclic process is always zero.
ΔU=0
Summary of Results
- (a) The net change in heat energy Q=4.61kJ
- (b) The net work done Wnet=4.61kJ
- (c) The net change in internal energy ΔU=0
2. Work Done in Segment AB (W_AB):
- For an isochoric process (constant volume), the work done is zero.
- Therefore, WAB=0.
- For an isothermal expansion, the work done can be calculated using the formula:
WBC=NRTln(PBPC)
- Given values: N=2 moles, R=8.32J/(mol K), TB=400K, PB=2PC (assumed).
- Substitute values:
WBC=2×8.32×400×ln(2)≈2×8.32×400×0.693≈4.61kJ
- For an isochoric process (constant volume), the work done is again zero.
- Therefore, WCA=0.
Wnet=WAB+WBC+WCA=0+4.61kJ+0=4.61kJ
Q=ΔU+W
- Since the process is cyclic, the net change in internal energy (ΔU) is zero.
- Therefore, Q=W.
Q=4.61kJ
- The net change in internal energy for a cyclic process is always zero.
ΔU=0
- (a) The net change in heat energy Q=4.61kJ
- (b) The net work done Wnet=4.61kJ
- (c) The net change in internal energy ΔU=0
Topper's Solved these Questions
- INTERNAL ENERGY BOOK - ICSECHAPTER - INTERNAL ENERGY EXERCISE - SELECTED PROBLEMS (FROM HEAT ENGINES)
21 Videos
- INTERNAL ENERGY BOOK - ICSECHAPTER - INTERNAL ENERGY EXERCISE - SELECTED PROBLEMS (FROM ISOTHERMAL AND ADIABATIC PROCESSES )
10 Videos
- GRAVITATIONBOOK - ICSECHAPTER - GRAVITATIONEXERCISE - FROM THE HUBBLE TELESCOP
2 Videos
- MOTION IN FLUIDS BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - SELECTED PROBLEMS (FROM POISEUILLE.S FORMULA)
19 Videos
Similar Questions
Two moles of helium gas undergo a cyclic process as shown in Fig. Assuming the gas to be ideal, calculate the following quantities in this process
(a) The net change in the heat energy
(b) The net work done
(c) The net change in internal energy
View SolutionTwo moles of helium gas undergo a cyclic process as shown in Fig. Assuming the gas to be ideal, calculate the following quantities in this process

(a) The net change in the heat energy
(b) The net work done
(c) The net change in internal energy
View Solution
Knowledge Check
Two moles of Helium gas undergo a reversible cyclic process as shown in figure. Assuming gas to be ideal, what is the net work involved in the cyclic process ?
 A200R ln2B100R ln2C300R ln2D400R ln2
A200R ln2B100R ln2C300R ln2D400R ln2Two moles of Helium gas undergo a reversible cyclic process as shown in figure. Assuming gas to be ideal, what is the net work involved in the cyclic process ?
 A200 Rln2B100 Rln2C300 Rln2D400 Rln2
A200 Rln2B100 Rln2C300 Rln2D400 Rln2
Two moles of helium gas undergo a cyclic process as shown in Fig. Assuming the gas to be ideal, calculate the following quantities in this process

(a) The net change in the heat energy
(b) The net work done
(c) The net change in internal energy
View SolutionTwo moles of Helium gas undergo a reversible cyclic process as shown in figure. Assuming gas to be ideal, what is the net work involved in the cyclic process ?

View SolutionA sample of helium is undergoing a cyclic process ABCA as shown. In which of the following processes heat is a absorbed by the gas?

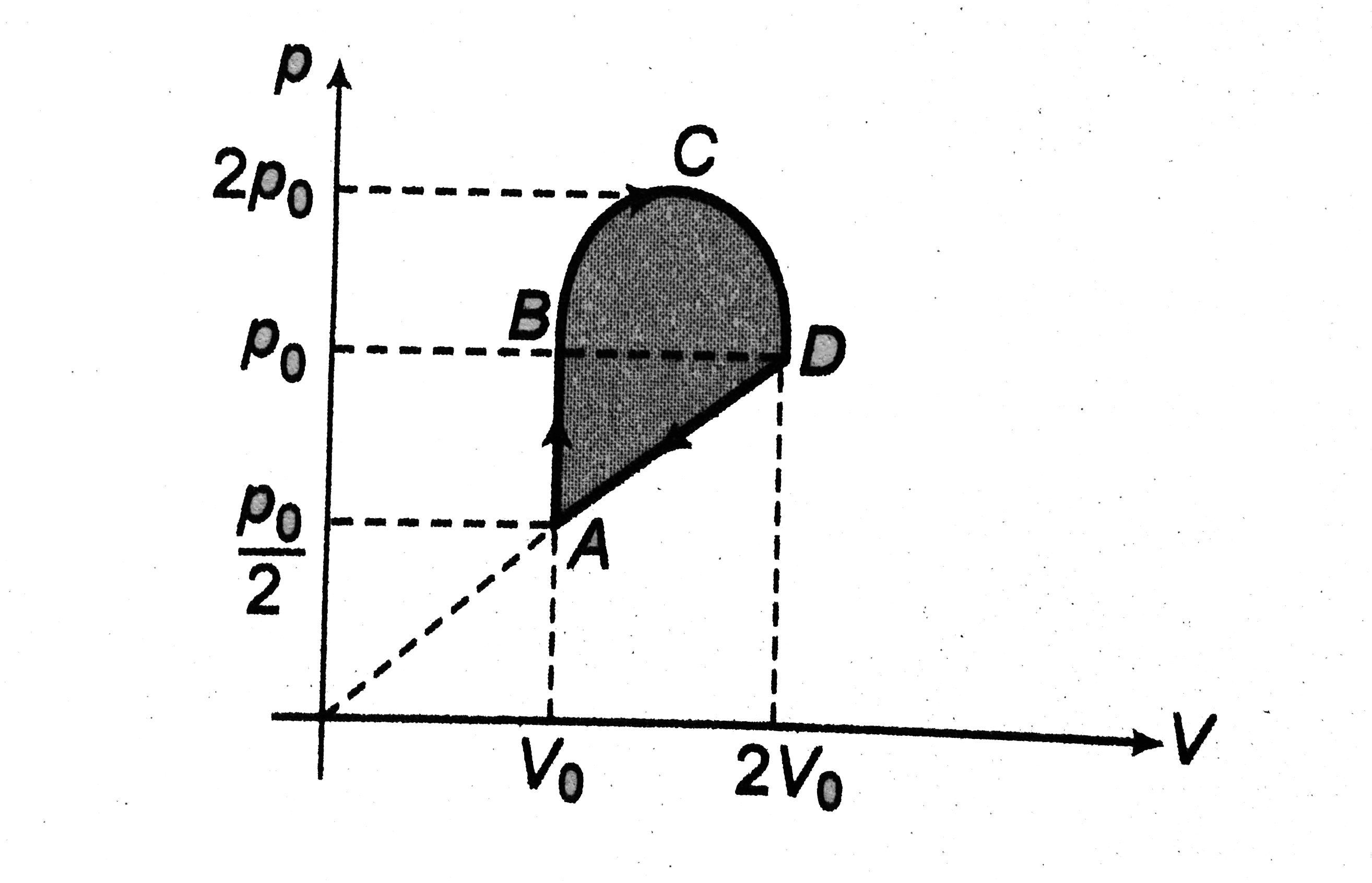
View SolutionTwo moles of a monatomic ideal gas undergo a cyclic process ABCDA as shown in figure. BCD is a semicircle. Find the efficiency of the cycle.
View SolutionTwo moles of an ideal gas are undergone a cyclic process 1-2-3-1. If net heat exchange in the process is 300J, the work done by the gas in the process 2-3 is

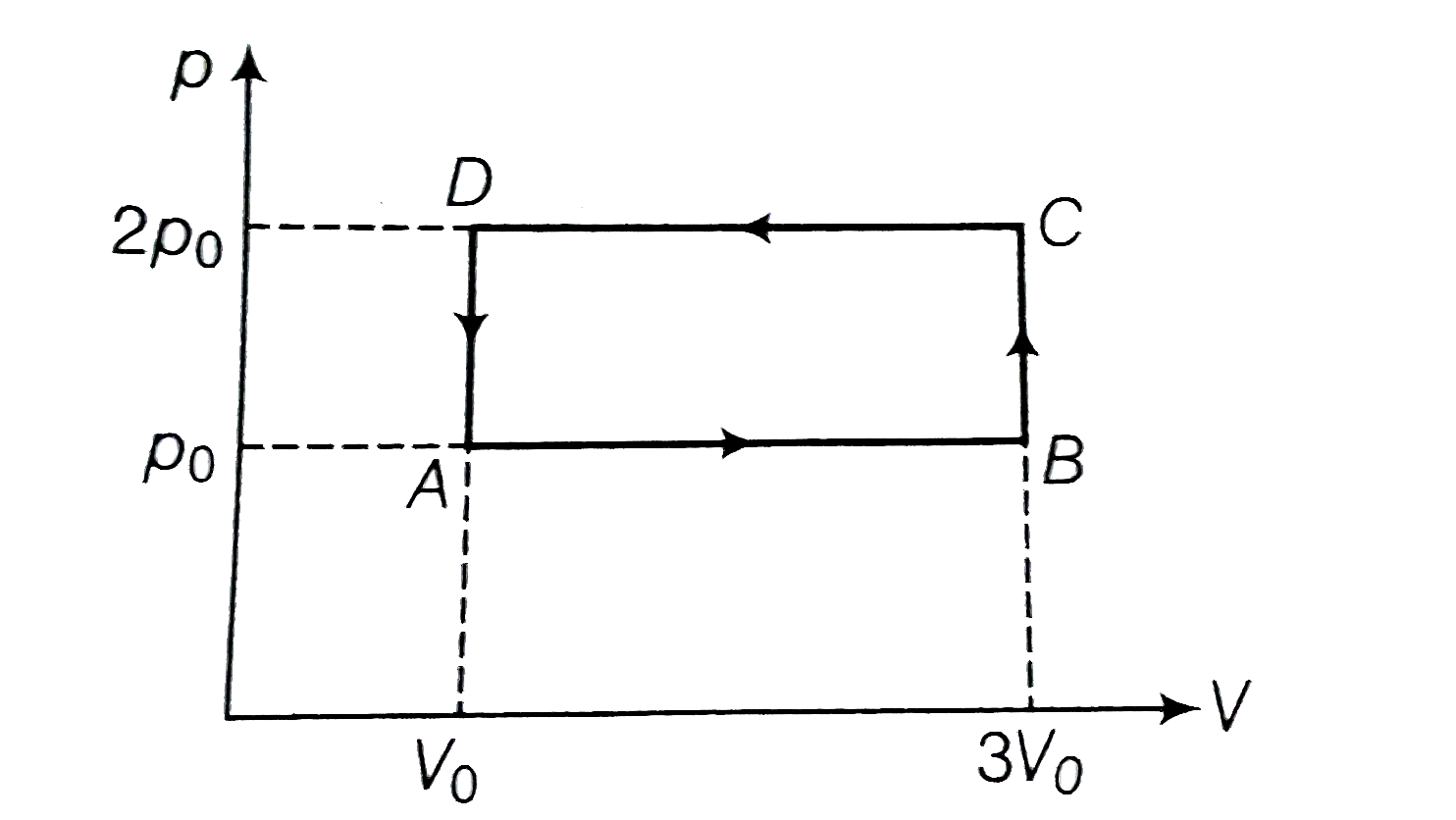
View SolutionAn ideal gas undergoes cyclic process ABCDA as shown in givend p−V diagram. The amount of work done by the gas is
View Solution