Two narrow cylindrical pipes AandB have the same length . Pipe A is open at both ends and is filled with a monoatomic gas of molar mass MA. Pipe B is open at one end and closed at the other end and is filled with a diatomic gas of molar mass MB. Both gases are at the same temperature .
a. If the frequency to the second harmonic of the fundamental mode in pipe A is equal to the frequency of the third harmonic of the fundamental mode in pipe B, determine the value of MA/MB.
b. Now the open end of pipe B is also closed ( so that pipe B is closed at both ends ). Find the ratio of the fundamental frequency in pipe A to that in pipe B.
a. If L is the length of each pipe AandB , then fundamental frequency of pipe A ( open at both ends )
nA=vA2L (i)
Fundamental frequency of pipe B ( closed at one end)
nB=vB4L (ii)
Given 2nA=3nB
2(vA2L)=3(vB4L)
⇒vAvB=34
But vA=√γARTAMA,vB=√γBRTBMB
Given TA=TB
For monoatomic get
γA=53
For diatomic get
γB=75
∴vAvB=√{γAγB)MBMA
√(5/3)(7/5)MBMA
=√2521MBMA
(i) From Eqs.(iii) and (iv)
√2521MBMA=34
(ii) MAMB=(43)2×2521=400189
b. When pipe B is closed at both ends , fundamental frequency of pipe B becomes
nB=vB2L (v)
Using Eqs. (i) ,(iii) and (v) , we get
iii. nAnB=vAvB=34
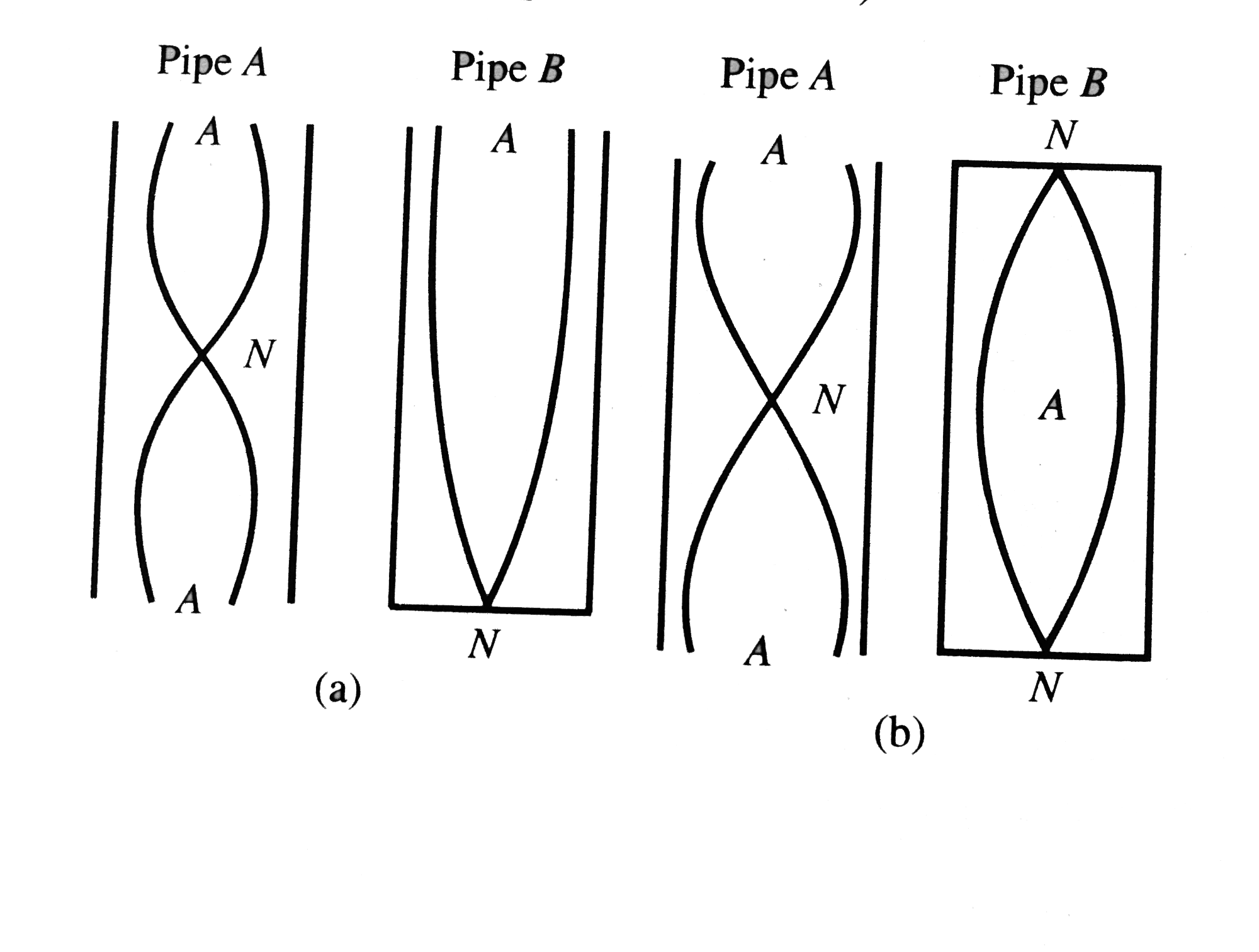
Similar Questions
Two narrow cylindrical pipes AandB have the same length. Pipe A is open at both ends and is filled with a monoatomic gas of molar mass MA. Pipe B is open at one end and closed at the other end, and is filled with a diatomic gas of molar mass MB. Both gases are at the same temperature.
(a) If the frequency of the second harmonic of the fundamental mode in pipe A is equal to the frequency of the third harmonic of the fundamental mode in pipe B, determine the value of MB/MB.
(b) Now the open end of pipe B is also closed (so that the pipe is closed at both ends). Find the ratio of the fundamental frequency in pipe A to that in pipe B.
View SolutionTwo narrow cylindrical pipes AandB have the same length. Pipe A is open at both ends and is filled with a monoatomic gas of molar mass MA. Pipe B is open at one end and closed at the other end, and is filled with a distomic gas of molar mass MB. Both gases are at the same tempreture.
(a) If the frequency of the second harmonic of the fundamental mode in pipe A is equal to the frequency of the third harmonic of the fundamental mode in pipe B, determine the value of MB/MB.
(b) Now the open end of pipe B is also closed (so that the pipe is closed at both ends). Find the ratio of the fundamental frequency in pipe A to that in pipe B.
View Solution
Knowledge Check
A pipe open at both ends gives frequencies which are
Aonly even multiples of fundamental frequency.Bonly odd multiples of fundamental frequency.Call integral multiples of fundamental frequency.Dall fractional multiple of fundamental frequency.What is the shortest length of a pipe open at one end and closed to other end resonates with the fundamental frequency n ?
A21Bv/2nC41Dv/4nThe fundamental frequency of a pipe closed at one end is 100Hz. If close end is open the fundamental frequency of same pipe wil be
A100 HzB200 HzC50 HzD400 Hz
Show that an organ pipe of length 2l open at both ends has the same fundamental frequency as another pipe of length I closed at one end.
View SolutionThe fundamental frequency of a pipe closed at one end is 100Hz. If close end is open the fundamental frequency of same pipe wil be
View SolutionIf the fundamental frequency of a pipe closed at one is 512HZ . The frequency of a pipe of the same dimension but open at both ends will be
View SolutionPipe A is 0.50 m long and open at both ends. Pipe B is open at one end and closed at the other end. Determine the length of pipe B so that it has the same fundamental frequency as A.
View SolutionIf the fundamental frequency of a pipe closed at one is 512HZ . The frequency of a pipe of the same dimension but open at both ends will be
View Solution
