Two optical media have a plane boundary between them. Suppose $θ_{1 c r}$ is the critical angle of incidence of a beam and $θ_{1}$ is the angle of incidence at which the refracted beam is perpendicular to the reflected one (the beam is assumed to come from an optically denser medium). Find the relective index of these media if ${sin θ}_{1 c r} / {sin θ}_{1} = η = 1.28$ .

Video Solution

Text Solution

Verified by Experts

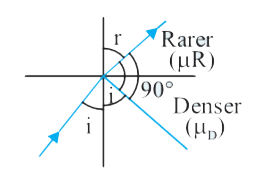
Let two optical mediums of $R . I . n_{1}$ an d $n_{2}$ respectively be such that $n_{1} > n_{2}$ . In the case when angle of incidence is $θ_{1 c r}$ (Fig.) from the law of refraction
$n_{1} {sin θ}_{1 c r} = n_{2}$ (1)
In the case, when the angle o fincidence is $θ_{1}$ , from the law of refraction at the interface o fmediums $1$ and $2$ .
$n_{2} {sin θ}_{1} = n_{2} {sin θ}_{2}$
But in accordance with the problem $θ_{2} = (π / 2 - θ_{1})$
so, $n_{1} {sin θ}_{1} = n_{2} {cos θ}_{1} (2)$
Dividing Eqn (1) and (2)
$\frac{{sin θ}_{1 c r}}{{sin θ}_{1}} = \frac{1}{{cos θ}_{1}}$
or, $η = \frac{1}{{cos θ}_{1}}$ , so ${cos θ}_{1} = \frac{1}{η}$ and ${sin θ}_{1} = \frac{\sqrt{η^{2} - 1}}{η}$ (3)
But $\frac{n_{1}}{n_{2}} = \frac{{cos θ}_{1}}{{sin θ}_{1}}$
So, $\frac{n_{1}}{n_{2}} = \frac{1}{η} \frac{η}{\sqrt{η^{2} - 1}}$ (Using 3)
Thus $\frac{n_{1}}{n_{2}} = \frac{1}{\sqrt{η^{2} - 1}}$

If $θ_{1}$ and $θ_{2}$ are the angles of incidence and reflection respectively, then correct relation between them is
A $θ_{1} = \frac{π}{2} + θ_{2}$
B $θ_{1} > θ_{2}$
C $θ_{1} < θ_{2}$
D $θ_{1} = θ_{2}$
Light from a denser medium 1 passes to a rarer medium 2. When the angle of incidence is $θ$ the partially reflected and refracted rays are mutually perpendicular. The critical angle will be

A ${sin}^{- 1} (cot θ)$
B ${sin}^{- 1} (tan θ)$
C ${sin}^{- 1} (cos θ)$
D ${sin}^{- 1} (sec θ)$
A beam of light travelling in water strikes a glass plate, which is also immersed in water. When the angle of incidence is $51^{\circ}$ , the reflected beam is found to be plane polarised . What is the refractive index of glass if the refractive index of water is $\frac{4}{3}$ ? $[{tan 51}^{\circ} = 1.235]$
A $1.646$
B $1.325$
C $2.123$
D $1.987$