Question

Two paarticles $1$ and $2$ are projected simultaneusly with velocities $v_1$ and $v_2$, respectively. Particle $1$ is projectected vertically up from the top of a cliff of heitht $h$ and particle $2$ is projected vertically up from the bottom of the cliff. If the bodies meet (a) above the top of the cliff, (b) between the top and bottom of the the cliff, and (c ) below the bottom of the cliff, find the time of meeting of the particles.
.

Explanation

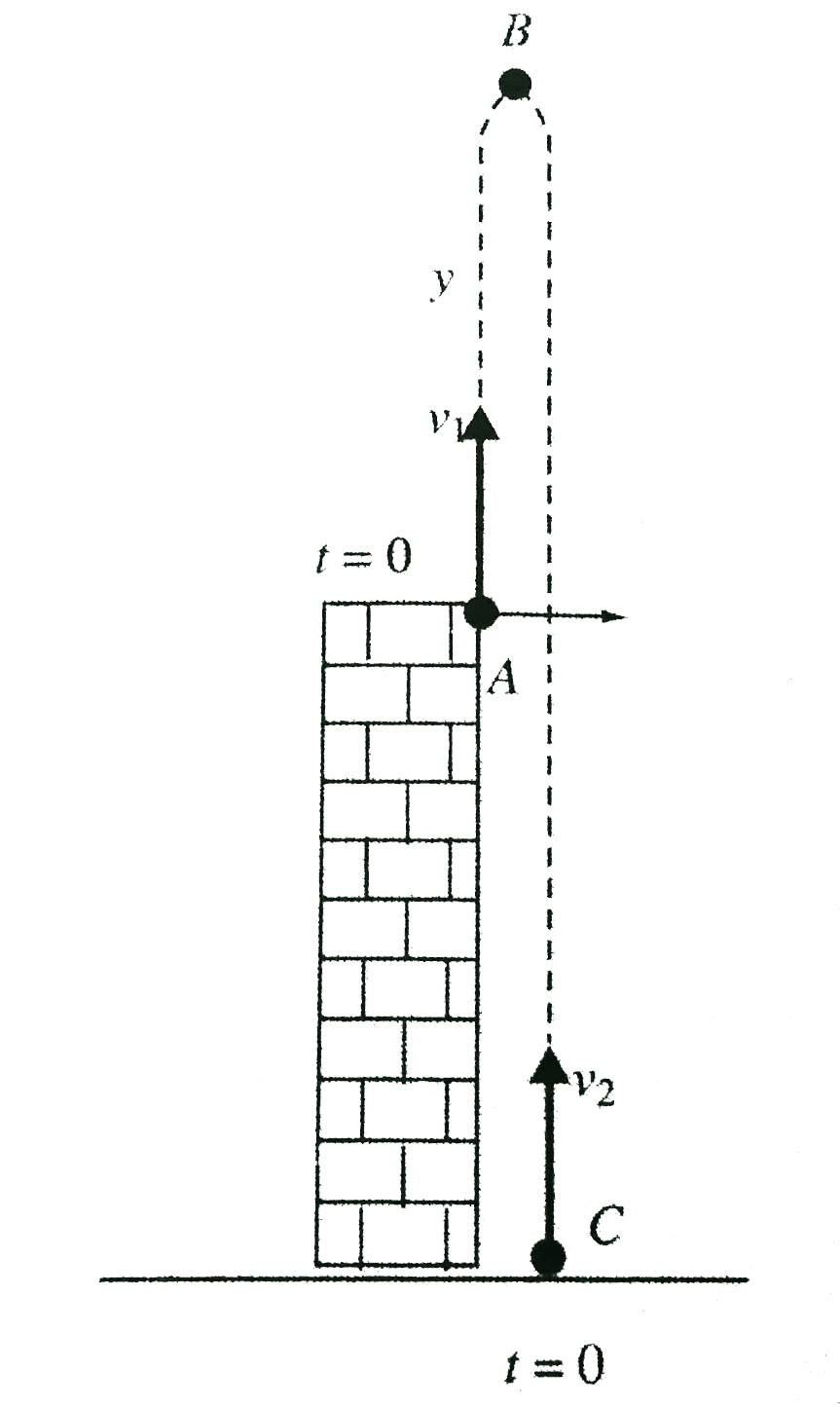
The point of collision above the top of the cliff. Let the particle meet after time`t`.
For first particle, `s=s_(1),v_(0)=v_(1),a=-g`.
Then, `s_(1)=v_(1)t-(1)/(2) g t^(2)` (ii)
For second particle, `s=s_(2),v_(0)=v_(2),a=-g`.
Referring to.
`s_(2)-s_(1)=h` (iii)
Substituting `s_(1)` from (i), `s_(2)` from (ii) in (iii), we have
`t=(h)/((v_(2)-v_(1)))`
.
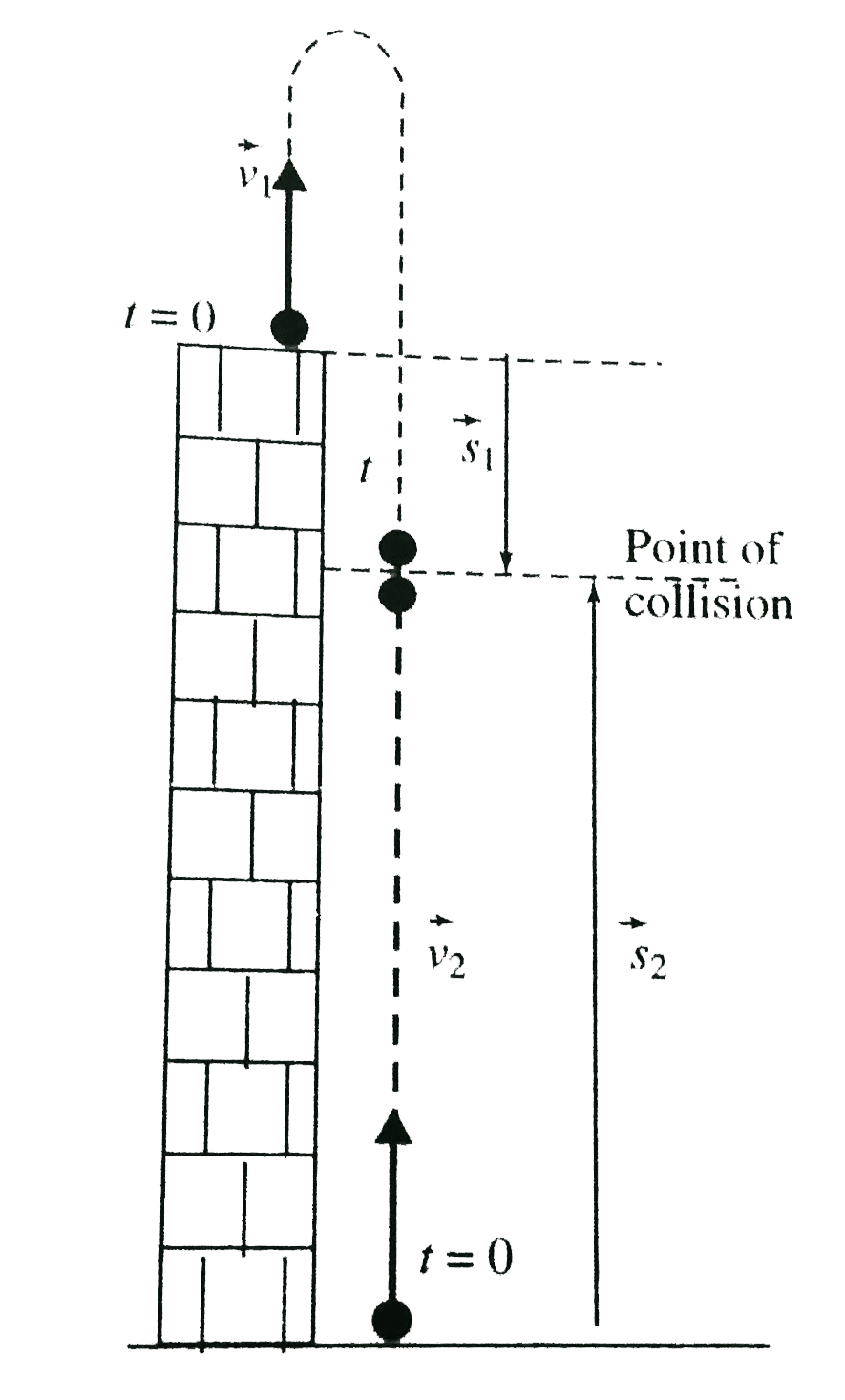
b. The point of collision of the paricle in between the top an battom of the cliff.
.
For the first particle, `s=-s_(1), v_(0)=v_(1)` and `a=-g`
Position-time relation for first particle,
`s_(1)=v_(1)t-(1)/(2) g t^(2)`
This gives `=(1)/(2)g t^(2)-v_(1)t` (i)
Similarly, for the second particle, `s=2_(2),v_(0)=v_(2)`, and `a=-g`.
Then `S_(2)=v_(2)t-(1)/(2)g t^(2)` (ii)
Referring to Find , `s_(1)+s_(2)=h`, (iii)
`t=(h)/((v_(2)-v_(1)))`
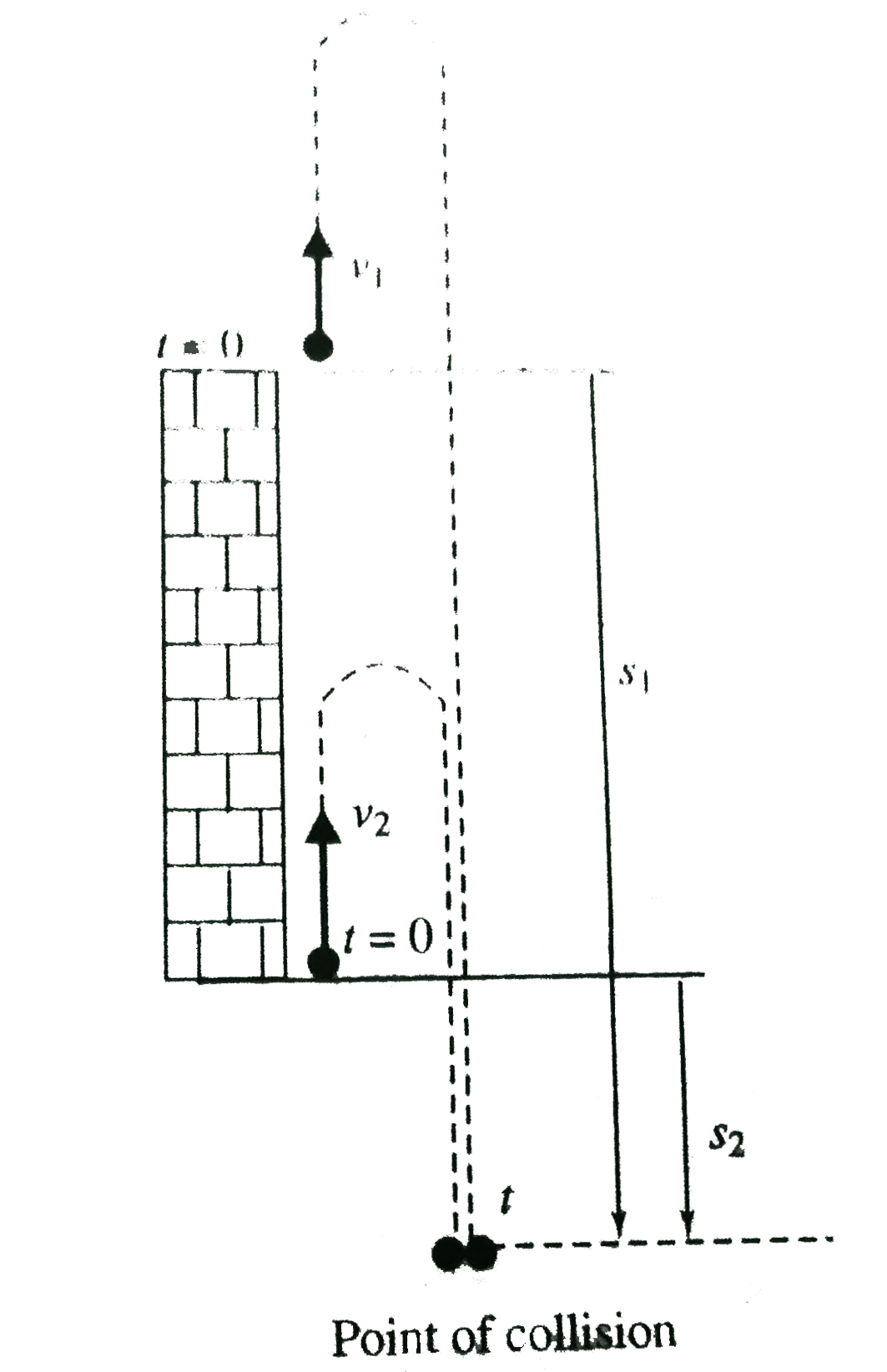
c. The point collision of the particles below the bottom of the cliff (let us assume a ditch at the base of base of the Cliff).
.
For article `1, s=-s_(1), v_(0)=v_(1)`, and `a=-g`.
Position-time relation for first particl
`-s_(1)=v_(1)t-(1)/(2)g t^(2)`
This gives `S_(1)=(1)/(2) g t^(2)-v_(1)t` (i)
Similarly, For particle (2), `=-s_(2),v_(0)=v_(2)`, and `a=-g`.
We have ` s_(2)=(1)/(2)g t^(2)-v_(2)t` (ii)
Substituting `s_(1)` from (i), `s_(2)` From (ii) in (iii), we have
`t=(h)/(v_(2)-v_(1))`.