Two parallel straight lines are inclined to the horizon at an angle . A particle is projected from a point mid way between them so as to graze one of the lines and strikes the other at right angle. Show that if is the angle between the direction of projection and either of lines, then .
Video Solution
Text Solution
A to B :
A to C : -h
And
Multiplying both sides by , we get
=.
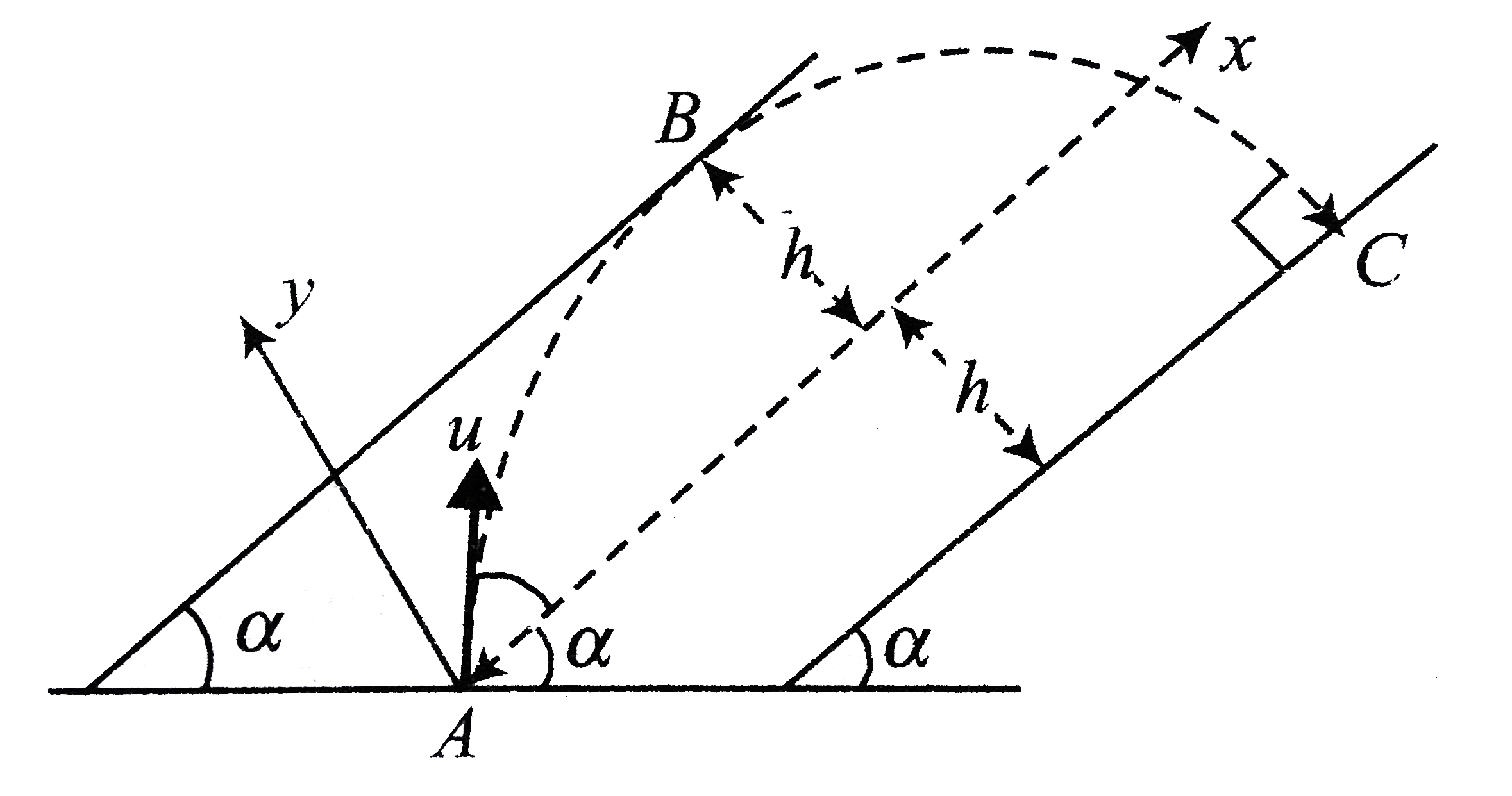 .
.
|
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Single Correct
76 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Multiple Correct
11 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.4
11 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
Knowledge Check
If θ is the angle between two regression lines with correlation coefficient γ, then :
Asinθ≥1−γ2Bsinθ≤1−γ2Csinθ≤γ2+1Dsinθ≤γ2−1If θ is the angle between two regression lines with correlation coefficient γ, then :
Asinθ≥1−γ2Bsinθ≤1−γ2Csinθ≤γ2+1Dsinθ≤γ2−1A particle is projected from a point A with velocity √2u an angle of 45∘ with horizontal as shown in figure. It strikes the plane BC at right angles. The velocity of the particle at the time of collision is
 A√3u2Bu2C2u√3Du
A√3u2Bu2C2u√3Du
The angle between the pair of straight lines y2sin2θ−xysinθ+x2(cos2θ−1)=0 is
View SolutionIf the angle between the two lines y2+kxy−x2tan2θ=0 is 2θ then k=
View SolutionA particle is projected from a point P with a velocity v at an angle θ with horizontal. At a certain point Q it moves at right angles to its initial direction. Then
View SolutionA particle is projected from the ground with an initial speed of v at an angle θ with horizontal. The average velocity of the particle between its point of projection and highest point of trajectroy is :
View SolutionA particle is projected with a velocity u from the foot of an inclined plane whose inclination to the horizon is β. It strikes. the plane at right angles if
View Solution
