two particals are thrown vertically upward with the same initial velocity of 50m/s but 2s apart. How long after the first one thrown, will they meet?
Let the particles meet t second after the projection of the first and at height h. The second particle will take time (t-2) second
Ist particle: h=50t−12gt2…(i)
IInd particle: h=50(t−2)−12g(t−2)2…(ii)
Equating (i) and (ii), we get
50t−12gt2=50(t−2)−12g(t−2)2
100=12g[t2−(t−2)2]
20=(2t−2)(2)⇒t=6s
h=50t−12gt2
=50×6−12×10(6)2=300−180=120m
Topper's Solved these Questions
Similar Questions
Two bodies are thrown verically upward, with the same initially velocity of 98m/s, but the second one is thrown 4 sec. after first is thrown. If after 4n seconds after the first particle is thrown, both of them meet then value of n is ?
View SolutionMatching type Question : For a body thrown vertically upwards with initial velocity u
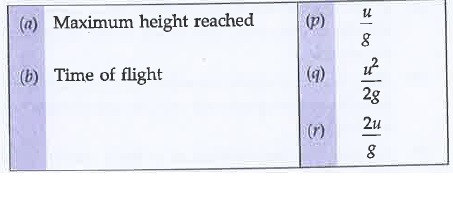 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A ball thrown vertically upwards with an initial velocity of 1.4m/s. The total displcement of the ball is
A22.4cmBzeroC44.8mD33.6m - Question 2 - Select One
Two stones are thrown vertically upwards with the same velocity of 49m/s. If they are thrown one after the other with a time lapse of 3 second, height at which they collide is
A58.8 mB111.5 mC117.6 mD122.5 m - Question 3 - Select One
A particle is thrown vertically upwards with a velocity of 490 cm/s. It will return to this position after
A1 sB0.5 sC2 sDnone of these
Two bodies are projected vertically upwards from one point with the same initial velocity v0. The second body is projected t0s after the first. How long after will the bodies meet?
View SolutionA ball is dropped from the top of a tower of height 100 m and another ball is thrown vertically upward at the same instant with a velocity of 10 m/s. Find the time after which the ball will be at same level.
View SolutionA ball is thrown vertically upward with a velocity of 20 m/s. Calculate the maximum height attain by the ball.
View SolutionA particle is thrown vertically upwards with a velocity of 490 cm/s. It will return to this position after
View SolutionA ball thrown vertically upwards with an initial velocity of 1.4 m/s returns in 2s. The total dispalcement of the ball is
View Solution

