Two particle each of mass M are fixed at positions (0, a) and (0,−a). Another particle of mass M/2 is thrown from origin along + z axis so that it is just able to reach a point (0,0,2√3a). Find the soeed with which it was projrcted.
The correct Answer is:⎡⎢⎣2 ⎷GMa((√13−1√13))⎤⎥⎦
Step by step video, text & image solution for Two particle each of mass M are fixed at positions (0, a) and (0, -a). Another particle of mass M//2 is thrown from origin along + z axis so that it is just able to reach a point (0, 0, 2sqrt(3)a). Find the soeed with which it was projrcted. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GRAVITATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GRAVITATIONEXERCISE - Discussion Qns
31 Videos
- GRAVITATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GRAVITATIONEXERCISE - Concetual MCQ
39 Videos
- GRAVITATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GRAVITATIONEXERCISE - Unsolved Numerical
94 Videos
- FLUID MECHANICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - FLUID MECHANICSEXERCISE - Unsolved Numerical Problems
86 Videos
- KINEMATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Unsolved Numerical Pro.
83 Videos
Similar Questions
Two particle of mass 1 kg and 2 kg are located at x = 0 and x = 3 m. Find the position of their centre of mass.

View SolutionA particle of mass m is thrown horizontally from the top of a tower and anoher particle of mass 2m is thrown vertically upward. The acceleration of centre of mass is
View Solution
Knowledge Check
Two small particles P and Q each of mass m are fixed along x-axis at points (a,0) and (-a,0). A third particle R is kept at origin. Then
Aif particle R is displaced along x-axis it will start oscillating.Boscillations of R along x-axis are simple harmonic in natureCif R is displaced of R along y-axis, it starts oscillatingDoscillations along y-axis may be simple harmonic in nature.Two particles of masses 1kg and 2kg are located at x=0 and x=3m. Find the position of their centre of mass.
A2m from 1 kgB2m from 2 kgC1m from 1 kgDnone of theseA particle of mass m is suspended from a string of length l fixed to the point O. What velocity should be imparted to the particle in its lowermost position so that the string is just able to reach the horizontal diameter of the circle?
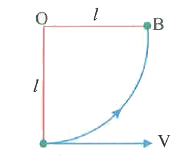 Av=√2glBv=√3glCv=√glDv=2gl
Av=√2glBv=√3glCv=√glDv=2gl
Two equal positive charges , Q , are fixed at points (0,d) and (0,−d) on the y-axis. A charged particle having charge −q and mass m is released from rest at point (d,0) on the x-axis . Discuss the motion of charged particle.
View SolutionTwo point charges each 50μC are fixed on y-axis at y=+4m and y=−4m. Another charged particle having charge −50μC and mass 20g is moving along the positive x-axis. When it is at x=−3m , its speed is 20m/sec. Find the speed of charged particle when it reaches to origin. Also , find distance of charged particle from origin , when its kinetic energy becomes zero.
View SolutionA number of particles each of mass 0.75kg are placed at distances 1m, 2m, 4m, 8m etc. from origin along positive X axis. the intensity of gravitational field at the origin will be -
View SolutionComprehension # 5
One particle of mass 1kg is moving along positive x-axis with velocity 3m/s. Another particle of mass 2kg is moving along y-axis with 6m/s. At time t=0,1kg mass is at (3m,0) and 2kg at (0,9m),x−y plane is the horizontal plane. (Surface is smooth for question 1 and rough for question 2 and 3)
The centre of mass of the two particles is moving in a straight line which equation is :-
View SolutionComprehension # 5
One particle of mass 1kg is moving along positive x-axis with velocity 3m/s. Another particle of mass 2kg is moving along y-axis with 6m/s. At time t=0,1kg mass is at (3m,0) and 2kg at (0,9m),x−y plane is the horizontal plane. (Surface is smooth for question 1 and rough for question 2 and 3)
Co-ordinates of centre of mass where it will stop finally are :-
View Solution
