Two particle of equal mass are projected simultaneously from the roof of a tower of height 20 m with same speed 20m//s, one horizontally and the other vertically upwards. Choose the correct alternative (s).
The acceleration of center of mass is g//2 downwards
The acceleration of centre of mass is g downwords
Maximum height of centre of mass centre of mass from the ground is 25 m
Maximum height of centre of mass from the ground is 40 m
To solve the problem, we need to analyze the motion of two particles projected from the top of a tower of height 20 m. One particle is projected horizontally with a speed of 20 m/s, and the other is projected vertically upwards with the same speed.
1. Identify the Initial Conditions:
- Height of the tower (h) = 20 m
- Speed of projection (u) = 20 m/s
- Mass of both particles (m1 = m2) = m (equal mass)
2. Determine the Acceleration of the Center of Mass:
- Both particles experience the same gravitational acceleration (g = 9.81 m/s² downward).
- The acceleration of the center of mass (ACM) can be calculated using:
ACM=m1a1+m2a2m1+m2
- Since both particles have the same mass and are subject to the same gravitational acceleration:
ACM=m⋅g+m⋅gm+m=2mg2m=g
- Therefore, the acceleration of the center of mass is g downward.
3. Calculate the Initial Height of the Center of Mass:
- Initially, both particles are at a height of 20 m.
- The center of mass (CM) is at:
hCM,initial=h1+h22=20+202=20 m
4. Determine the Maximum Height of the Center of Mass:
- For the particle projected vertically upwards, we need to find the maximum height it reaches.
- The vertical component of the center of mass velocity (V_y) is given by:
Vy,CM=m1⋅Vy1+m2⋅Vy2m1+m2
- Here, Vy1=20 m/s (upward) and Vy2=0 m/s (horizontal):
Vy,CM=m⋅20+m⋅0m+m=20m2m=10 m/s
5. Using the Kinematic Equation to Find Maximum Height:
- At maximum height, the final vertical velocity (V_y) is 0. Using the equation:
V2y=V2y,CM−2gh
- Setting Vy=0:
0=(10)2−2gh⟹100=2gh⟹h=1002g
- Substituting g≈10 m/s2:
h=10020=5 m
6. Calculate the Total Maximum Height of the Center of Mass:
- The center of mass rises 5 m above its initial height of 20 m:
hCM,max=hCM,initial+h=20+5=25 m
Conclusion:
- The maximum height of the center of mass from the ground is 25 m.
- The acceleration of the center of mass is g (downward).
- Height of the tower (h) = 20 m
- Speed of projection (u) = 20 m/s
- Mass of both particles (m1 = m2) = m (equal mass)
- Both particles experience the same gravitational acceleration (g = 9.81 m/s² downward).
- The acceleration of the center of mass (ACM) can be calculated using:
ACM=m1a1+m2a2m1+m2
- Since both particles have the same mass and are subject to the same gravitational acceleration:
ACM=m⋅g+m⋅gm+m=2mg2m=g
- Therefore, the acceleration of the center of mass is g downward.
- Initially, both particles are at a height of 20 m.
- The center of mass (CM) is at:
hCM,initial=h1+h22=20+202=20 m
- For the particle projected vertically upwards, we need to find the maximum height it reaches.
- The vertical component of the center of mass velocity (V_y) is given by:
Vy,CM=m1⋅Vy1+m2⋅Vy2m1+m2
- Here, Vy1=20 m/s (upward) and Vy2=0 m/s (horizontal):
Vy,CM=m⋅20+m⋅0m+m=20m2m=10 m/s
- At maximum height, the final vertical velocity (V_y) is 0. Using the equation:
V2y=V2y,CM−2gh
- Setting Vy=0:
0=(10)2−2gh⟹100=2gh⟹h=1002g
- Substituting g≈10 m/s2:
h=10020=5 m
- The center of mass rises 5 m above its initial height of 20 m:
hCM,max=hCM,initial+h=20+5=25 m
- The maximum height of the center of mass from the ground is 25 m.
- The acceleration of the center of mass is g (downward).
Similar Questions
A particle of mass 50 g is projected horizontally from the top of a tower of height 50 m with a velocity 20m/s. If g=10m/s2, then find the :-
View SolutionTwo particles are projected simultaneously from two towers of different heights,one is horizontal with speed 10 m/s and the other at an angle 45° below the horizontal with speed v as shown in figure. The velocity v for which particles collides in air is

View SolutionTwo particles of equal mass are projected simultaneously with speeds 20m/s end 10√3m/s as shown in figure. Find the maximum height reached by the centre of mass of the particles
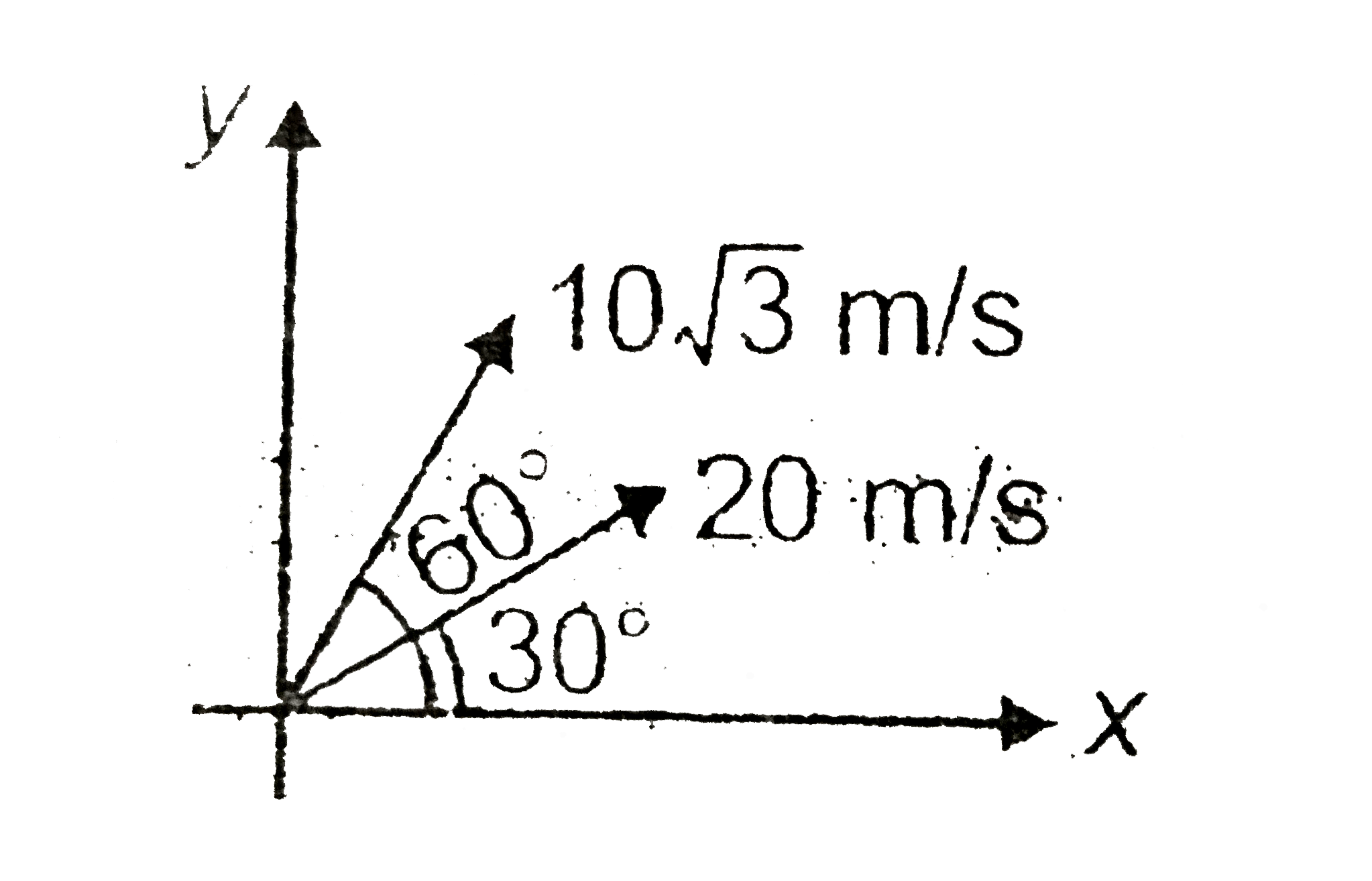
View SolutionTwo particles are projected with speed 4m/s and 3m/s simultaneously from same point as shown in the figure. Then:

View SolutionTwo particles are projected simultaneously from the same point, with the same speed, in the same vertical plane, and at different angles with the horizontal in a uniform gravitational field acting vertically downwards. A frame of reference is fixed to one particle. The position vector of the other particle , as observed from this frame, is →r. Which of the following statement is correct?
View SolutionTwo balls of equal mass are projected from a tower simultaneously with equal speeds. One at angle θ above the horizontal and the other at the same angle θ below the horizontal. The path of the center of mass of the two balls is
View SolutionA particle is projected upwards from the roof of a tower 60 m high with velocity 20m/s. Find
(a) the average speed and
(b) average velocity of the particle upto an instant when it strikes the ground. Take g=10m/s2
View SolutionTwo balls of equal mass are projected upwards simultaneously, one from the ground with initial velocity 50ms−1 and the other from a 40m tower with initial velocity of 30ms−1. The maximum height attained by their COM will be a) 80 m b) 60 m c) 100 m d) 120 m
View SolutionTwo particles A and B are projected simultaneously from two towers of heights 10 m and 20m respectively. Particle A is projected with an initial speed of 10√2m/s at an angle of 45∘ with horizontal, while particle B is projected horizontally with speed 10m/s. If they collide in air, what is the distance d between the towers?
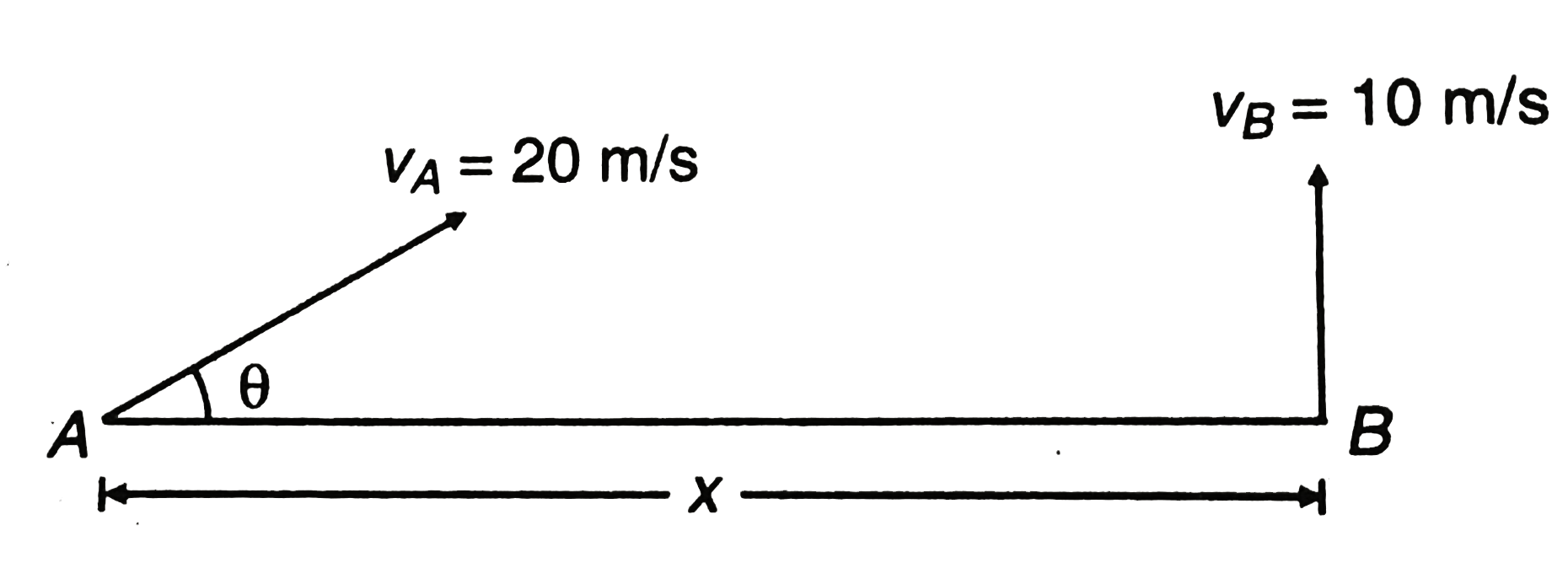
View SolutionTwo balls are projected simultaneously with the same speed from the top of a tower-one upwards and the other downwards.If they reach the ground in 6s and 2s ,the height of the tower is
View Solution
