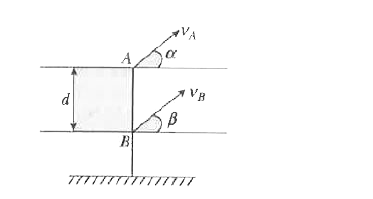
Two particles A and B are thrown simultaneously from two different floors of tower having distance d between them. Velocities of particle A is vA at angle α from horizontal while velocities of particle B is vB at an angle β from horizontal. If two particles collide in mid-air, then vAvB.
cosβcosα
sinαsinβ
tanαtanβ
cotαcotβ
The correct Answer is:A
Step by step video, text & image solution for Two particles A and B are thrown simultaneously from two different floors of tower having distance d between them. Velocities of particle A is v_(A) at angle alpha from horizontal while velocities of particle B is v_(B) at an angle beta from horizontal. If two particles collide in mid-air, then v_(A)/v_(B). by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)3videos
MOTION IN TWO AND THREE DIMENSIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (LINKED COMPREHENSION)14videos
MOTION IN TWO AND THREE DIMENSIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PROBLEMS50videos
MOTION IN TWO AND THREE DIMENSIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( Integer Type )3videos
MOTION ALONG A STRAIGHT LINE
- BOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Practice Questions57videos
OSCILLATIONS
Similar Questions
Two particles A and B are thrown simultaneously from two different floors of tower having distance d between them.Velocitiy of particle A is vA at angle α from horizontal while velocity of particle B is vB at an angle β from horizontal.If two particles collide in mid-air,then find vAvB.
View SolutionA particle is thrown with speed u at an angle α with horizontal from the ground. After how much time, the velocity of particle will make an angle β with horizontal.
View Solution
Knowledge Check
- Question 1 - Select One
Two particles are projected simultaneously from the top of the towers as shown. Find the distance between the towers if they collide in mid air during their flight.
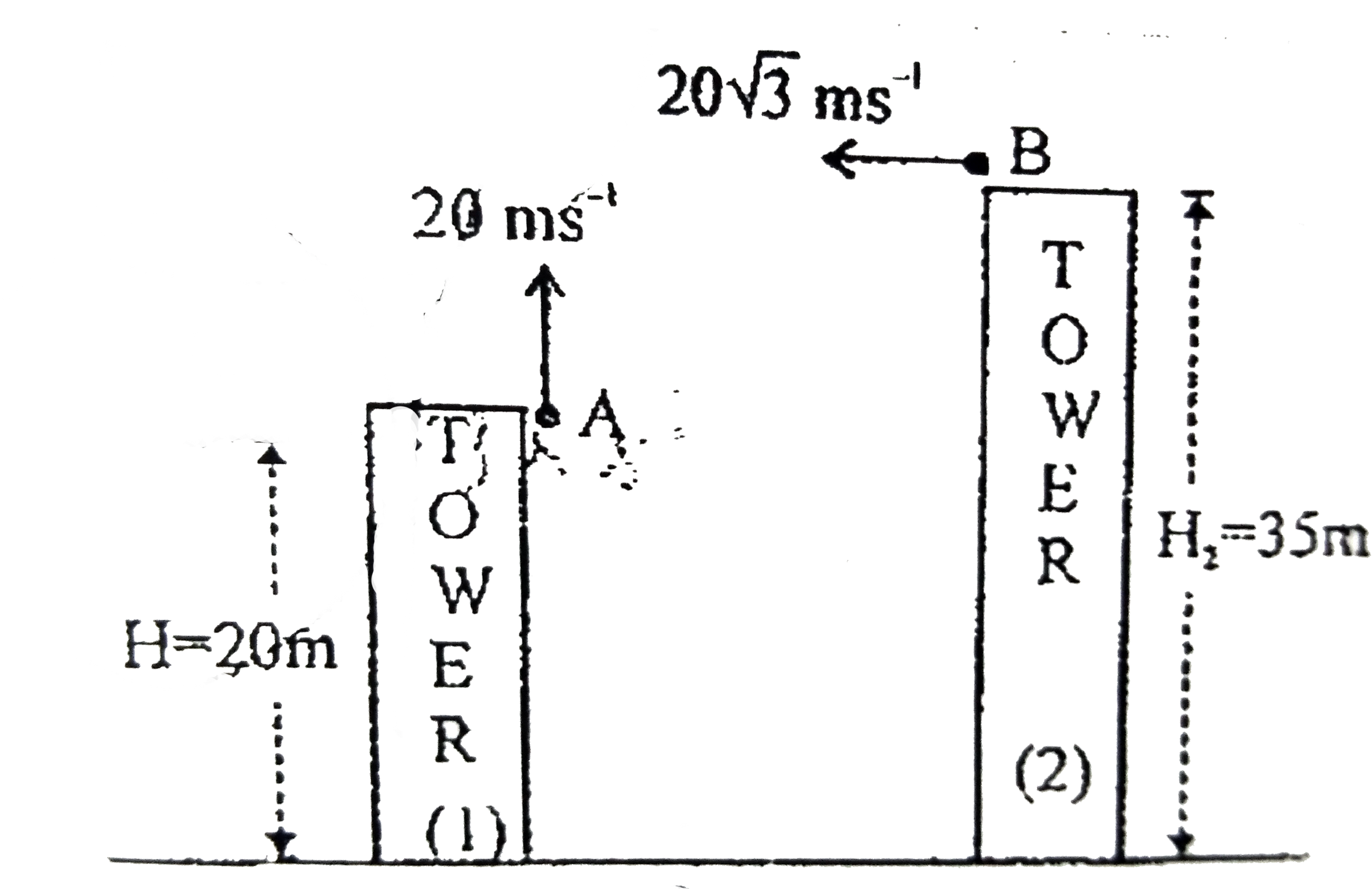 A15mB20mC15√3mD5√3m
A15mB20mC15√3mD5√3m - Question 2 - Select One or More
Two particles of different masses are thrown simultaneously in air. Centre of mass of two balls while both are in mid air.
AMove in a straight line independent of initial velocities of particlesBMove in straight line when both the particles are thrown along same vertical lineCHave acceleration equal to gDHave acceleration depending on initial velocities of particles - Question 3 - Select One
A particle is thrown with a speed u at an angle θ with the horizontal. When the particle makes an angle ϕ with the horizontal. Its speed changes to v :
Av=ucosθBv=ucosθ.cosϕCv=ucosθ.secϕDv=usecθ.cosϕ
Two particles are simultaneously projected in the same vertical plane from the same point with velocities u and v at angles αandβ with horizontal. Find the time that elapses when their velocities are parallel.
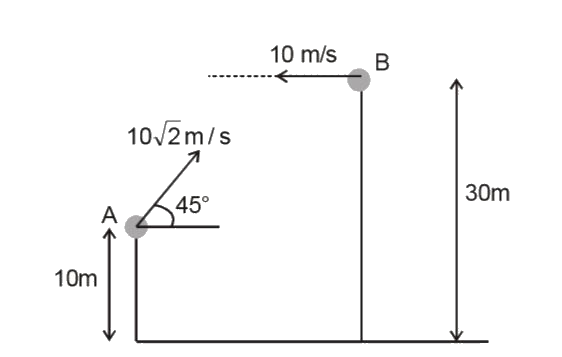
View SolutionTwo particles A and B are projected simultaneously from two towers of heights 10 m and 20m respectively. Particle A is projected with an initial speed of 10√2m/s at an angle of 45∘ with horizontal, while particle B is projected horizontally with speed 10m/s. If they collide in air, what is the distance d between the towers?
 View Solution
View SolutionA particle is thrown with speed u of an angle theta with the horizontal when the particle makes an angle phi with the horizontal its speed changes to v
View SolutionTwo projectiles are projected simultaneously from two towers as shwon in figure. If the projectiles collide in the air, then find the distance "s" between the towers.
 View Solution
View SolutionTwo projectiles are thrown simultaneously in the same plane from the same point. If their velocities are v1 and v2 at angles θ1 and θ2 respectively from the horizontal, then ansewer the following questions
The trajectory of particle 1 with respect to particle 2 wil beView Solution

