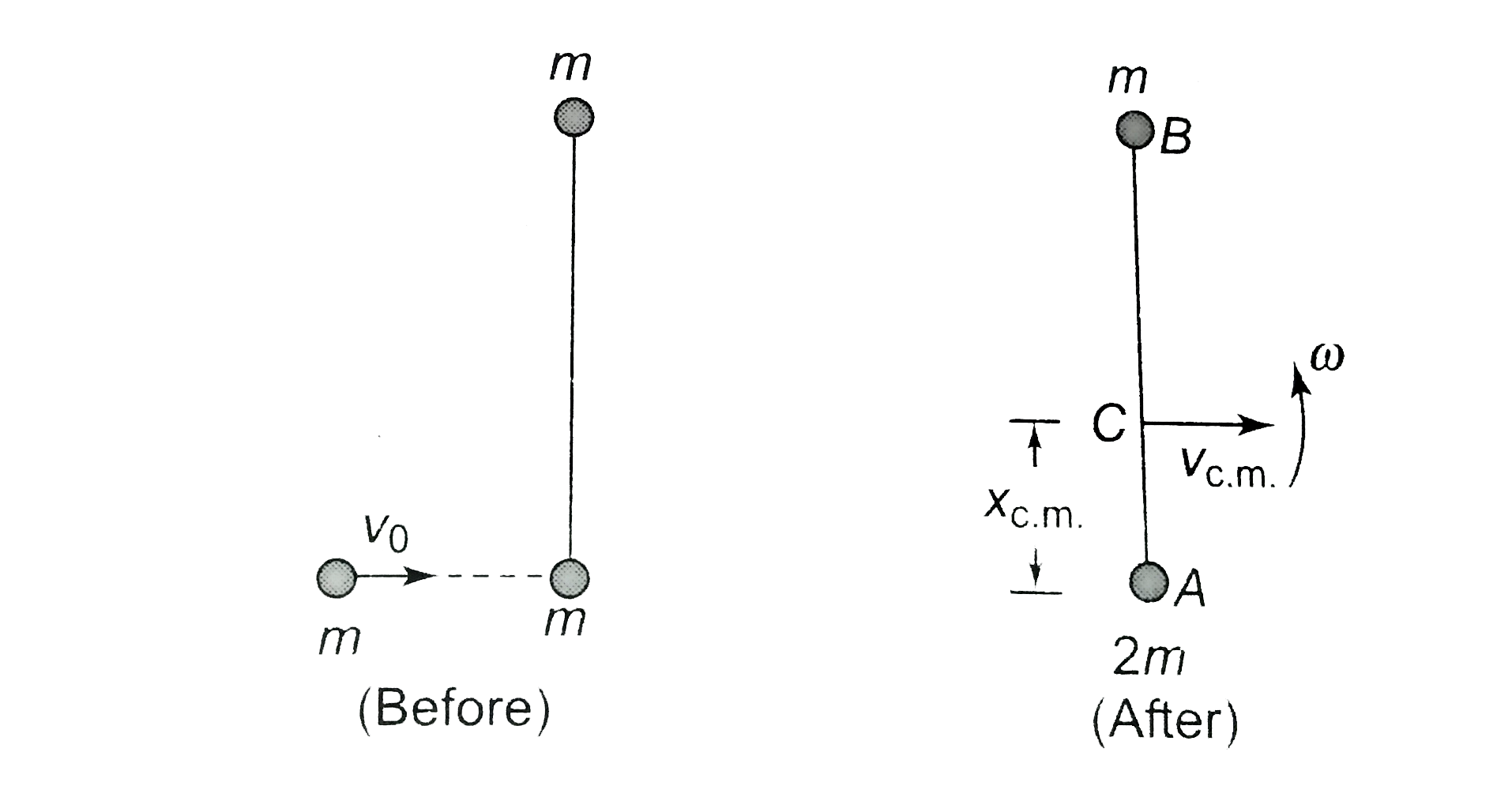
Two particles A and B, each of mass m, are connected by a light rod of length L lying on a smooth horizontal surface. A particle of mass m moving with speed v0 strikes to the end of rod and sticks to A as shown . Find
(a) the velocity of the center of mass,
(b) the angular velocity about the center of mass of system (A+B+ particle) and
(c) the linear speeds of A and B immediately after collision.

When the particle sticks to A, the location of center of mass
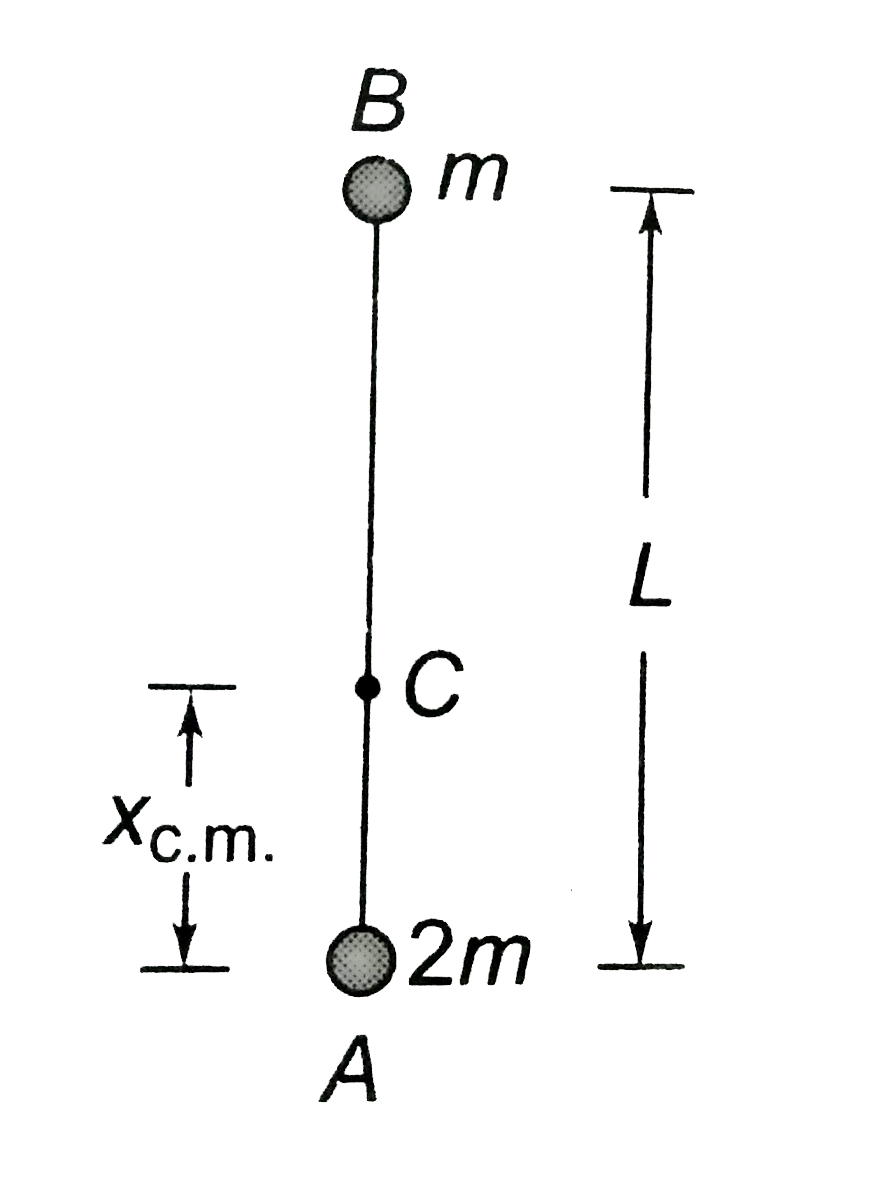
xc.m.=2m×0+m×L2m+m=L3
Conservation of linear momentum
mv0=(2m+m)vc.m.⇒vc.m.=v03
Conservation of angular momentum about C
mv0xc.m.=Icω
mv0L3=[2mx2c.m.+m(L−xc.m.)2]ω
=[2m(L3)2+m(2L3)2]ω
=23mL2ω⇒ω=v02L
linear speed of
A:vA=vc.m.+xc.m.ω=v03+L3×v02L=v02
B:vB=vc.m.−(L−xc.m.)ω=v03−2L3×v02L=0
Topper's Solved these Questions
Similar Questions
A uniform rod of mass M and length L lies on a frictionless horizontal plane. A particle of same mass M moving with speed v0 perpendicular to the length of the rod strikes the end of the rod and sticks to it. Find the velocity of the center of mass and the angular velocity about the center of mass of (rod + particle) system.
View SolutionA uniform rod of mass M and length L lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance L/6 from the center and stops after the collision. Find
(a) the velocity of center of mass of rod and
(b) the angular velocity of the rod about its center just after collision.View Solution
Knowledge Check
- Question 1 - Select One
A uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the centre of mass C and the angular, velocity of the system about the centre of mass after the collision.A2mvM+m,3Mv(M+2m)LBMvM+m,6Mv(M+4m)LC2mvM+m,3Mv(M+4m)LDmvM+m,6Mv(M+4m)L - Question 2 - Select One
A uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision. Find the velocity of the centre of mass C of the system constituting 'the rod plus the particle'.
A2MvM−mB2mvM+mCMvM+mDmvM+m - Question 3 - Select One
A uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the rod with respect to C before the collisionAMvM+mBmvM+mC2mvM+mD2MvM+m
A rod of mass M and length L is kept on a frictionless horizontal floor. A particle of mass m moving perpendicular to the rod with a speed v strikes at the end of the rod and sticks there. Calculate angular velocity acquired by the combined system.
View SolutionA uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a4 from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.
View SolutionA uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the angular momentum of the particle and of then about the centre of mass C before the collision.View SolutionA uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the particle with respect to C before the collisionView Solution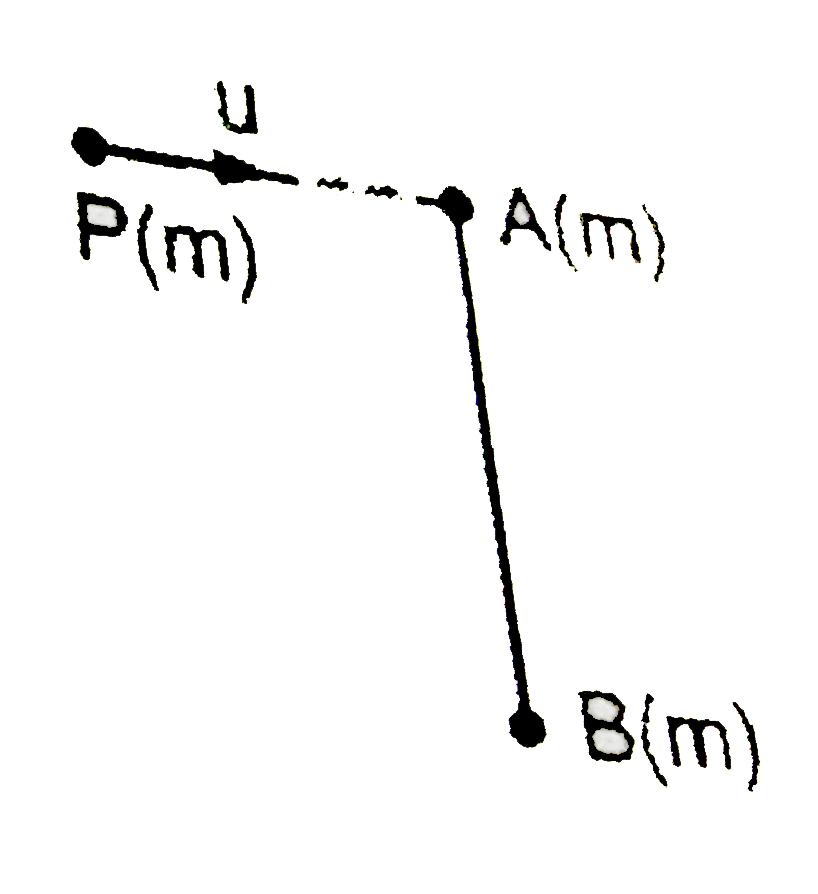
Two particle A and B, of mass m each, are joined by a rigid massless rod of length l. A particle P mass m, moving with a speed u normal to AB, strikes A and sticks to it. The centre of mass of the 'A+B+P' system is C.View Solution

