Two particles start simulataneously from the same point and moves along two straight lines inclined at angle α, one with uniform velocity v0 and other from the rest with uniform acceleration, a0. After how much time their relative velocity is minimum and what is it equal to?
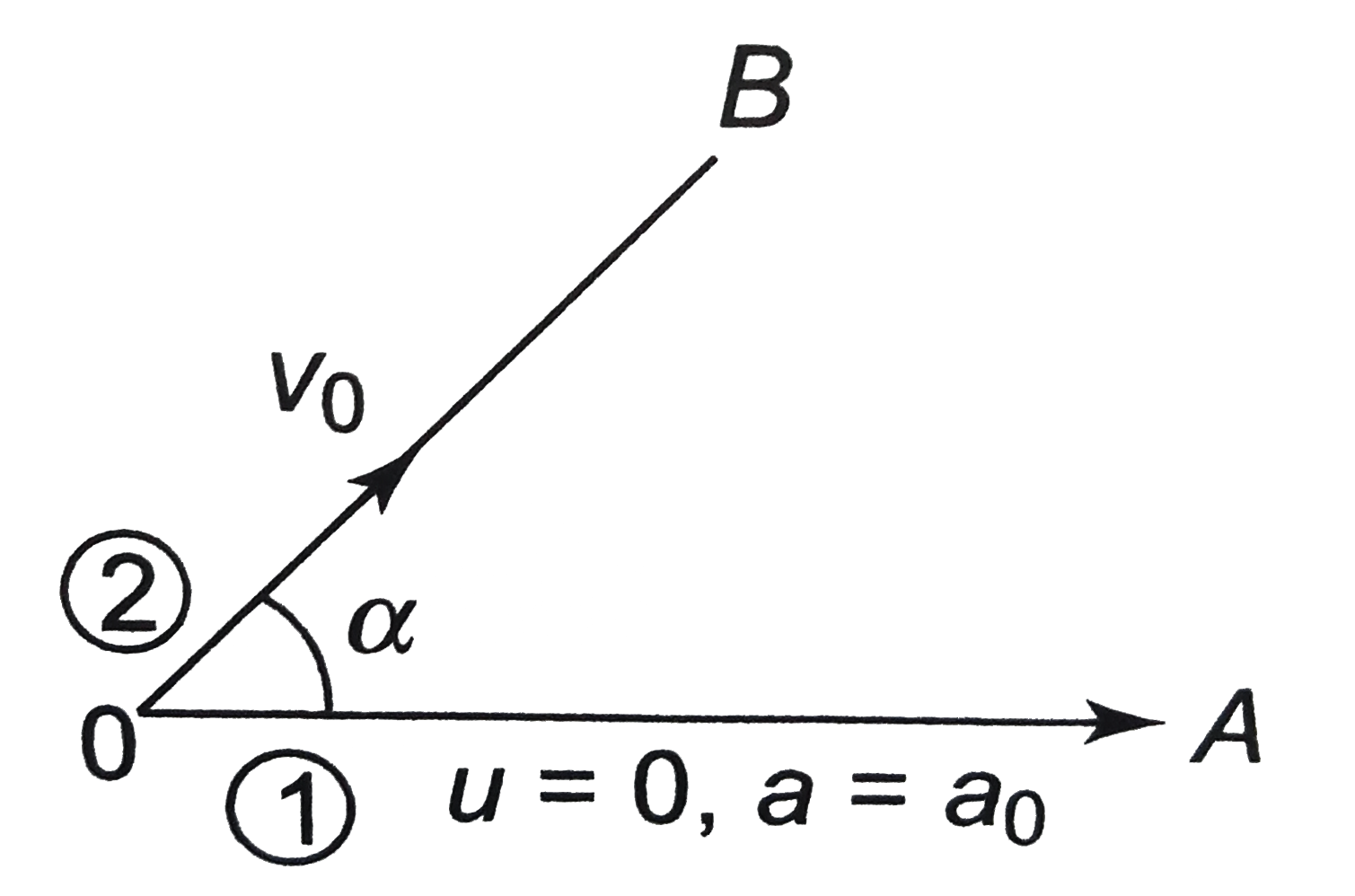
After time t,v1=u+at=a0t=v1/g
v2=v0=v2/g
v1/2=resultant of (velocity of 1 and velocity of 2 in opposite direction)

(v1/2)2=v20+(a0t)2+2(v0)(a0t)cos(180−α)
For (v1/2) to be minimum
d(v1/2)dt or d(v21/2)dt=0
⇒(2a0t)a0−2v0a0cosα=0
t=v0cosαa0
(v1/2)min=√v20+(v0cosα)2+2v0(v0cosα)(−cosα)
=v0sinα
Relative velocity is minimum after time v0cosαa0 and equal to v0sinα.
Topper's Solved these Questions
Similar Questions
Two cacar starts together from the asme point and move along two straight lines inclined at an angle θ, one moving with velocity (u) and the other from rest with a uniform acceleration (a). Show that the least relative velocity between then is usinθ and it occurs after a time t=(ucosθ)/a.
View SolutionTwo particles starts simultaneously from a point O and move along line OP and OQ, one with a uniform velocity 10m/s and other from rest with a constant acceleration 5m/s2 repectively. Line OP makes an angle 37∘ with the line OQ. Find the time at which they appear to ecah other moving at minimum speed?
View Solution
Knowledge Check
Two particles start simultaneously from a point with equal velocities v each along two straight inclined at 60∘. Find their relative velocity
AVB2VCV2D3VTwo particles start simultaneously from the same point and move along two straight lines. One with uniform velocity v and other with a uniform acceleration a. if α is the angle between the lines of motion of two particles then the least value of relative velocity will be at time given by
AvasinαBvacosαCvatanαDvacotαTwo particles start moving simultaneously from points (0, 0) and (1, 0) respectively in the OXY plane with uniform velocities v1 and v2 as shown in the figure. It is found that they collide. Then
 Av1=v2√2Bv1=v2Cv2=√2v1Dv2=v1√32
Av1=v2√2Bv1=v2Cv2=√2v1Dv2=v1√32
A person travelling on a straight line moves with a uniform velocity v1 for some time and with uniform velocity v2 for the next equal time. The average velocity v is given by
View SolutionA particle starting from rest moves along a straight line with constant acceleration for this velocity displacement graph will have the form-
View SolutionA particle starts from rest at t=0 and moves in a straight line with an acceleration as shown below. The velocity of the particle at t=3 s is

View SolutionA particle starts from rest at t=0 and moves in a straight line with an acceleration as shown below. The velocity of the particle at t=3 s is

View SolutionTwo particles start moving from the same point along the same straight line. The first moves with constant velocity v and the second with constant acceleration a. During the time that elapses before the sound catches the first, the greatest distance between the particle is.
View Solution
