Two plates $1$ and $2$ move with velocities $- v$ and $2 v$ respectively. If the sphere does not slide relative to the plates, assuming the masses of each body as $m$ , find the kinetic energy of the system (plates+sphere).

Video Solution

Text Solution

Verified by Experts

Top point of sphere in having velocity $v (\leftarrow)$ and bottom point in moving with $2 v (\to)$
We can find position of $I R C$
$\frac{y}{v} = \frac{2 R - y}{2 v} = y = \frac{2}{3} R$

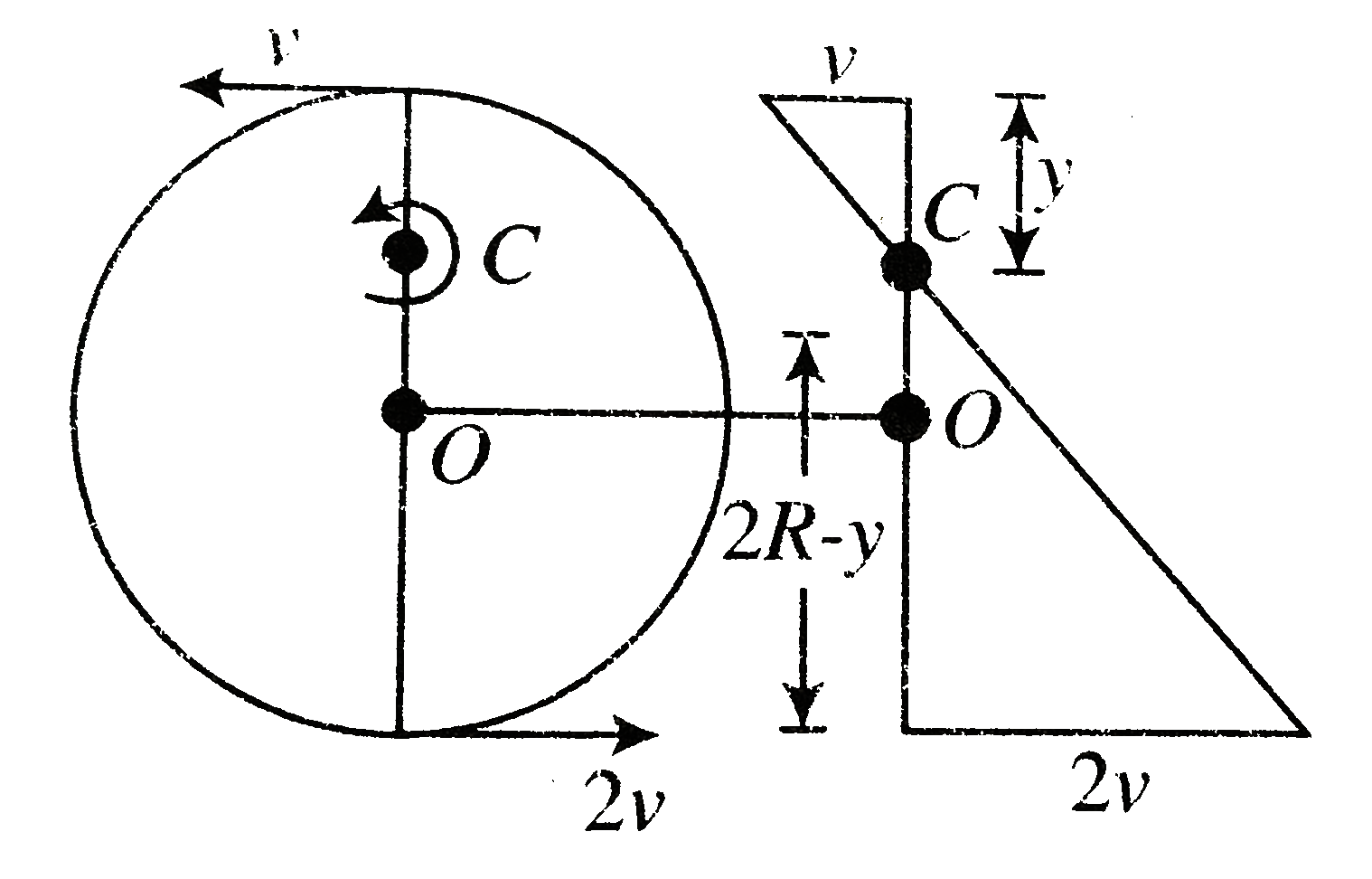
Hence we can assure the sphere will have pure rotation about $C (I C R)$
Hence the motion sphere can be considered as pure rotation about $C$ .
The angular velocityi of shere $ω = \frac{v}{y} = \frac{3 v}{2 R}$
The kinetic energy of sphere $k_{rotation} = \frac{1}{2} I_{C} ω^{2}$
$\Rightarrow k_{rotatioal} = \frac{1}{2} [\frac{2}{5} m R^{2} + m {(O C)}^{2}] ω^{2}$
$O C = R - \frac{2}{3} R = \frac{R}{3}$
$K_{rotational} = \frac{1}{2} (\frac{23}{45} m R^{2}) ω^{2} = \frac{23}{90} m ω^{2} R^{2}$
$= \frac{23}{90} m {(\frac{3 v}{2 R})}^{2} R^{2} = \frac{23}{40} m v^{2}$
Hence total kinetic energy
$K_{total} = \frac{1}{2} m v^{2} + \frac{1}{2} m {(2 v)}^{2} + \frac{23}{40} m v^{2} = \frac{123}{40} m v^{2}$

Updated on:21/07/2023

Two identical particles move towards each other with velocity 2v and v respectively. The velocity of centre of mass is
A $v$
B $\frac{v}{3}$
C $\frac{v}{2}$
Dzero.
Two identical particles move towards each other with velocity 2v and v respectively. The velocity of centre of mass is
AV
B $V / 3$
C $V / 2$
DZero
Two identical particles move towards each other with velocity 2v and v, respectively. The velocity of the centre of mass is:
Av
B $v / 3$
C $v / 2$
Dzero