Two point charges each 50μC are fixed on y-axis at y=+4m and y=−4m. Another charged particle having charge −50μC and mass 20g is moving along the positive x-axis. When it is at x=−3m , its speed is 20m/sec. Find the speed of charged particle when it reaches to origin. Also , find distance of charged particle from origin , when its kinetic energy becomes zero.
Let the speed of particle at origin be v. Applying energy conservation between A and O , we get
KA+UA=Ko+Uo
KA+(−Q)VA=Ko+(−Q)Vo
12mv2A+(−Q)14π∈0.2Q√32+42=12mv2o
+(−Q)14π∈0(14−15)
=2(50×10−6)2×9×109×120
12×20×10−3(v2o−202)=2.25
⇒v2o−400=225⇒v2o=625
vo=25m/sec
Applying energy conservation between A and B , we have
KA+UA=KB+UB
KA+(−Q)VA=0+(−Q)VB
12mv2A+(−Q)14π∈0.2Q5=(−Q)14π∈0.1√42+x2
12mv2A=14π∈02Q2[15−1√42+x2
12×20×10−3×(20)2=9×109×2×(50×10−6)2[15−1√42+x2]
4=45(15−1√16+x2)
⇒1√16+x2=15−445=545=19
x=√65m
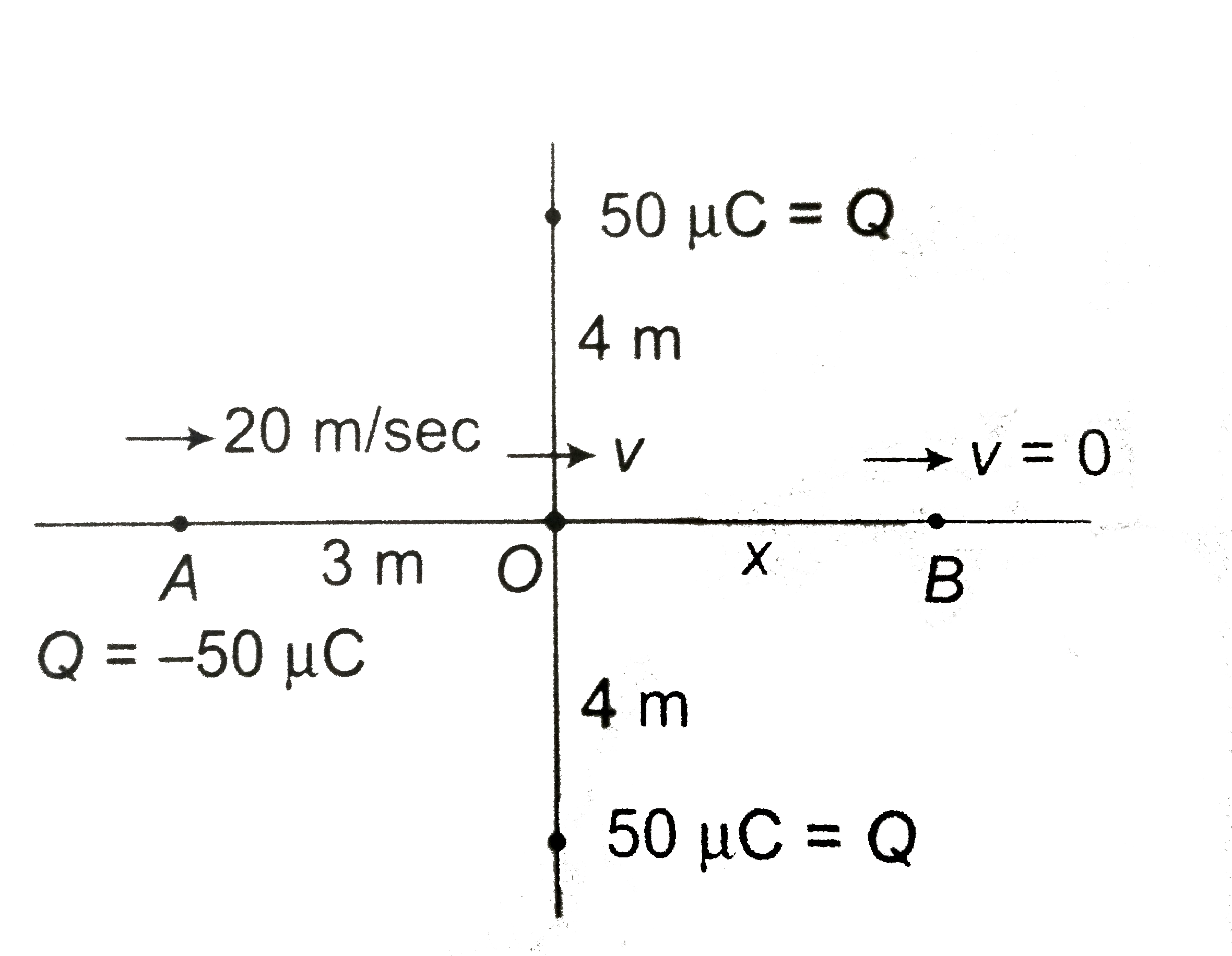
Topper's Solved these Questions
Similar Questions
Two equal positive charges , Q , are fixed at points (0,d) and (0,−d) on the y-axis. A charged particle having charge −q and mass m is released from rest at point (d,0) on the x-axis . Discuss the motion of charged particle.
View SolutionA particle having mass 2 kg is moving along straight line 3x+4y=5 with speed 8m/s . Find angular momentum of the particle about origin, x and y are in meters.
View Solution
Knowledge Check
Two charged particles having charges 1and−1μC and of mass 50g each are held at rest while their separation is 2m. Now the charges are released. Find the speed of the particles when their separation is 1m.
A15ms−1B35ms−1C310ms−1D27ms−1Two charged particles having charge 1μC and −μC and of mass 50gm each are held ar rest while their separtion is 2m. Find the relative velocity of the particles when their separation is 0.5m.
A15m/sB√35m/sC3√35m/sD3√310m/sConsider two positive point charges, each of magnitude q, placed on the y-axis at the points (0, a) and (0, -a). A positively charged particle of charge q' and mass m is displaced slightly from the origin in the direction of the positive x-axis.
Speed of charge q' at infinity isA√qq'πε0mB√q'πε0amC√qq'ε0amD√qq'πε0am
A charged particle of charge 1 mC and mass 2g is moving with a speed of 5m/s in a uniform magnetic field of 0.5 tesla. Find the maximum acceleration of the charged particle
View SolutionTwo point charge (Q each) are placed at (0,y) and (0,-y). A point charge q of the same polarity can move along X-axis. Then :
View SolutionConsider two positive point charges, each of magnitude q, placed on the y-axis at the points (0, a) and (0, -a). A positively charged particle of charge q' and mass m is displaced slightly from the origin in the direction of the positive x-axis.
At the origin, charge q' will be in
View SolutionTwo point charges (Q each are placed at (0,y) and (0-y) A point charge q of the sme polarity can move along the x-axis. Then
View SolutionA charged particle (charge q, mass m) has velocity v0 at origin in +x direction. In space there is a uniform magnetic field B in -z direction. Find the y coordinate of particle when is crosses y axis.
View Solution
