Two point charges +q and −q are held fixed at (−d,o) and (d,0) respectively of a x-y coordinate system. Then
(a) The electric field E at all points on the x-axis has the same direction
(b) Electric field at all points on y-axis is along x-axis
(c) Work has to be done in bringing a test charge from ∞ to the origin
(d) The dipole moment is 2qd along the x-axis
The correct Answer is:B
To solve the problem involving two point charges +q and −q located at coordinates (−d,0) and (d,0) respectively, we will analyze the dipole moment, electric field, and work done in bringing a test charge from infinity to the origin.
1. Identify the Charges and Their Positions:
- The positive charge +q is located at (−d,0).
- The negative charge −q is located at (d,0).
2. Calculate the Dipole Moment:
- The dipole moment →p is given by the formula:
→p=q⋅→d
- The distance →d between the charges is 2d (from −d to d).
- Therefore, the dipole moment is:
→p=q⋅(2d)^i=2qd^i
- The direction of the dipole moment is from the negative charge to the positive charge, which is along the negative x-axis.
3. Determine the Electric Field Along the X-Axis:
- The electric field →E at any point on the x-axis due to the charges can be calculated using the principle of superposition.
- For a point P on the x-axis, the electric field due to +q is directed away from the charge, while the field due to −q is directed towards the charge.
- The net electric field will depend on the position of point P relative to the charges.
4. Analyze the Electric Field on the Y-Axis:
- At any point on the y-axis, the electric field contributions from both charges will have components that result in a net electric field along the x-axis.
- This means that at all points on the y-axis, the resultant electric field will be directed along the x-axis.
5. Calculate Work Done in Bringing a Test Charge from Infinity to the Origin:
- The work done W in bringing a test charge q0 from infinity to a point in an electric field is given by:
W=q0(V∞−V0)
- The potential V at a point due to a point charge is given by:
V=kqr
- At the origin (0,0), the contributions from both charges cancel each other out, resulting in a net potential of zero:
V0=0
- At infinity, the potential is also zero:
V∞=0
- Therefore, the work done is:
W=q0(0−0)=0
Conclusion:
- The dipole moment is directed along the negative x-axis.
- The electric field at all points on the y-axis is directed along the x-axis.
- The work done in bringing a test charge from infinity to the origin is zero.
- The positive charge +q is located at (−d,0).
- The negative charge −q is located at (d,0).
- The dipole moment →p is given by the formula:
→p=q⋅→d
- The distance →d between the charges is 2d (from −d to d).
- Therefore, the dipole moment is:
→p=q⋅(2d)^i=2qd^i
- The direction of the dipole moment is from the negative charge to the positive charge, which is along the negative x-axis.
- The electric field →E at any point on the x-axis due to the charges can be calculated using the principle of superposition.
- For a point P on the x-axis, the electric field due to +q is directed away from the charge, while the field due to −q is directed towards the charge.
- The net electric field will depend on the position of point P relative to the charges.
- At any point on the y-axis, the electric field contributions from both charges will have components that result in a net electric field along the x-axis.
- This means that at all points on the y-axis, the resultant electric field will be directed along the x-axis.
- The work done W in bringing a test charge q0 from infinity to a point in an electric field is given by:
W=q0(V∞−V0)
- The potential V at a point due to a point charge is given by:
V=kqr
- At the origin (0,0), the contributions from both charges cancel each other out, resulting in a net potential of zero:
V0=0
- At infinity, the potential is also zero:
V∞=0
- Therefore, the work done is:
W=q0(0−0)=0
- The dipole moment is directed along the negative x-axis.
- The electric field at all points on the y-axis is directed along the x-axis.
- The work done in bringing a test charge from infinity to the origin is zero.
Topper's Solved these Questions
- BOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ELECTROSTATICSEXERCISE - Subjective Problems2videos
ELECTROSTATICS
- BOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ELECTROSTATICSEXERCISE - Comprehension Based Questions2videos
ELECTROSTATICS
- BOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTEXERCISE - JEE Main And Advanced107videos
ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENT
- BOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MODERN PHYSICSEXERCISE - MCQ (One Correct Answer1videos
MODERN PHYSICS
Similar Questions
Two point charges of magnitude +qand−q are placed at (−d/2,0,0)and(d/2,0,0) are respectively. Find the equation of the euipotential surface where the potential is zero.
View Solution" Two point charges "+2q" and "-q" are placed on "x" -axis at "(0,0,0)" and "(3,0,0)" respectively,How many points of zero electric potential are there in the plane "X=5?
View Solution
Knowledge Check
- Question 1 - Select One
Two point charges+q nd -q are held fixed at (−a,0) and (a,0) respectively of a x-y coordinate system then
Athe electric field E at all point on the axis has the same direction.BE at all points on the y-axis is along ˆiCpositive work is done in bringing a test charge from infinity to the originDAll of the above - Question 2 - Select One
A two point charges 4q and -q are fixed on the x - axis x=−d2andx=d2 , respectively. If a third point charge 'q' is taken from the origin to x = d along the semicircle as shown in the figure, the energy of the charge will
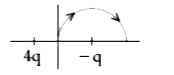 Aincrease by 2q23πε0dBdecrease by 4q23πε0dCincrease by 3q24πε0dDdecrease by q24πε0d
Aincrease by 2q23πε0dBdecrease by 4q23πε0dCincrease by 3q24πε0dDdecrease by q24πε0d - Question 3 - Select One
There are four point charges +q,−q,+q and −q are placed at the corners A,B,C and D respectively of a square of side a. The potential energy of the system is 14πε0 times
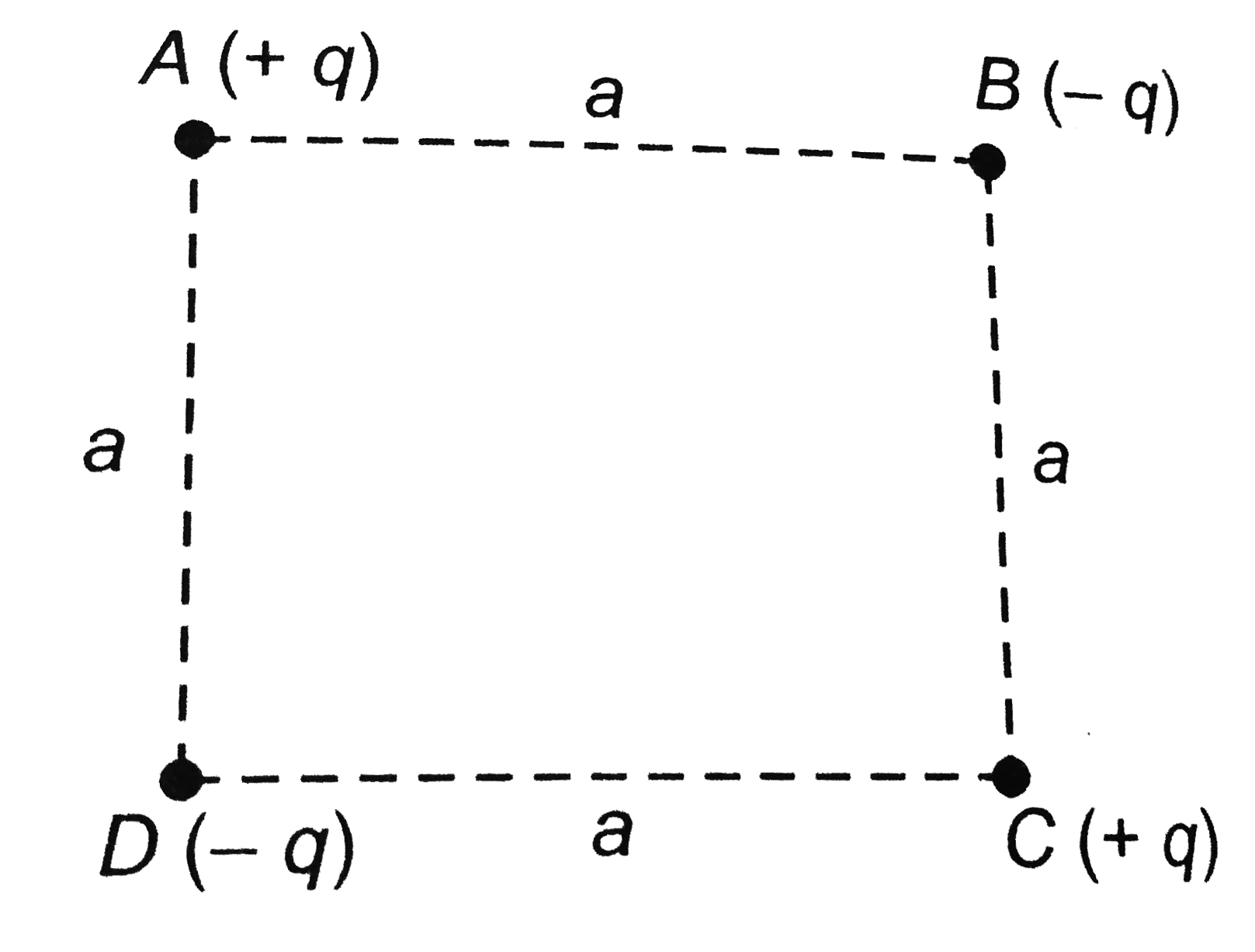 Aq2a(−4+√2)Bq22a(−4+√2)C4q2aD−4√2q2a
Aq2a(−4+√2)Bq22a(−4+√2)C4q2aD−4√2q2a
Two charges q1andq2 are placed at (0,0,d) and (0,0,-d) respectively. Find locus of points where the potential is zero.
View SolutionTwo charges q1andq2 are placed at (0,0,d) and (0,0,-d) respectively. Find locus of points where the potential is zero.
View SolutionTwo charges q1andq2 are placed at (0,0d)and(0,0−d) respectively. Find locus of points where the potential is zero.
View SolutionTwo point charges +8q and −2q are located at x=0 and x=L respectively. The location of a point on the x axis at which the net electric field due to these two point charges is zero is
View SolutionTwo point charges q and –q are at positions (0,0,d) and (0,0, –d) respectively . What is the electric field at (a,0,0 ) ?
View Solution

