Two point masses of 0.3 kg and 0.7kg are fixed at the ends of a rod of length 1.4 m and of negligible mass. The rod is set rotating about an axis perpendicular to its length with a uniform angular speed. The point on the rod through which the axis should pass in order that the work required for rotation of the rod is minimum, is located at a distance of
0,42 m from mass of 0.3 kg
0.70 m form mass of 0.7 kg
0.98 m form mass of 0.3 kg
0.98 m from mass of 0.7 kg
The correct Answer is:C
To solve the problem, we need to find the position along the rod where the axis of rotation should be placed to minimize the work required for rotation. We have two point masses, m1=0.3kg and m2=0.7kg, located at the ends of a rod of length L=1.4m.
1. Define the Position of the Axis:
Let the distance from the 0.3kg mass to the axis of rotation be x. Consequently, the distance from the 0.7kg mass to the axis will be L−x=1.4−x.
2. Kinetic Energy Calculation:
The kinetic energy KE of the system when rotating about the axis can be expressed as:
KE=12m1ω2r21+12m2ω2r22
where r1=x and r2=1.4−x. Thus,
KE=12(0.3)ω2x2+12(0.7)ω2(1.4−x)2
3. Simplifying the Kinetic Energy Expression:
Factor out ω22:
KE=ω22(0.3x2+0.7(1.4−x)2)
Expanding the second term:
KE=ω22(0.3x2+0.7(1.96−2.8x+x2))
=ω22(0.3x2+1.372−1.96x+0.7x2)
=ω22((0.3+0.7)x2−1.96x+1.372)
=ω22(x2−1.96x+1.372)
4. Finding the Minimum Work:
To minimize the kinetic energy, we take the derivative of KE with respect to x and set it to zero:
d(KE)dx=ω22(2x−1.96)=0
Solving for x:
2x−1.96=0⟹2x=1.96⟹x=0.98m
5. Conclusion:
The axis of rotation should be placed at a distance of 0.98m from the 0.3kg mass.
Final Answer:
The point on the rod through which the axis should pass in order that the work required for rotation of the rod is minimum, is located at a distance of 0.98 m from the 0.3kg mass.
Let the distance from the 0.3kg mass to the axis of rotation be x. Consequently, the distance from the 0.7kg mass to the axis will be L−x=1.4−x.
The kinetic energy KE of the system when rotating about the axis can be expressed as:
KE=12m1ω2r21+12m2ω2r22
where r1=x and r2=1.4−x. Thus,
KE=12(0.3)ω2x2+12(0.7)ω2(1.4−x)2
Factor out ω22:
KE=ω22(0.3x2+0.7(1.4−x)2)
Expanding the second term:
KE=ω22(0.3x2+0.7(1.96−2.8x+x2))
=ω22(0.3x2+1.372−1.96x+0.7x2)
=ω22((0.3+0.7)x2−1.96x+1.372)
=ω22(x2−1.96x+1.372)
To minimize the kinetic energy, we take the derivative of KE with respect to x and set it to zero:
d(KE)dx=ω22(2x−1.96)=0
Solving for x:
2x−1.96=0⟹2x=1.96⟹x=0.98m
The axis of rotation should be placed at a distance of 0.98m from the 0.3kg mass.
The point on the rod through which the axis should pass in order that the work required for rotation of the rod is minimum, is located at a distance of 0.98 m from the 0.3kg mass.
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ROTATIONAL MOTIONEXERCISE - MCQs with one correct answer
1 Videos
- MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MOTIONEXERCISE - JEE Main And Advanced
63 Videos
- SIMPLE HARMONIC MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - JEE Main And Advanced
69 Videos
Similar Questions
Point masses m1 and m2 are placed at the ends of a rigid rod of length L and negligible mass. The rod is to be set rotating about an axis perpendicular to its length. Locate a point on the rod through which the axis of rotation should pass in order that the work required to set the rod rotating with angular velocity ω0 is minimum.
View SolutionFind radius of gyration of a rod of length l and mass m about an axis perpendicular its length through one end.
View Solution
Knowledge Check
Two point masses A of mass M and B of mass of 4M are fixed at the ends of a rod of length l and of negligible mass. The rod is set rotation about an axis perpendicular to its length with a uniform angular speed. The work required for rotating the rod will be minimum when the distance of axis of rotation from the mass A is at
A25lB85lC45lDl5Point masses m1andm2 are placed at the opposite ends of a rigid rod of length L, and negligible mass. The rod is to be set rotating about an axis perpendicualr to it. The position of point P on this rod through which the axis should pass so that the work required to set the rod rotating with angular velocity ω0 is minimum, is given by :
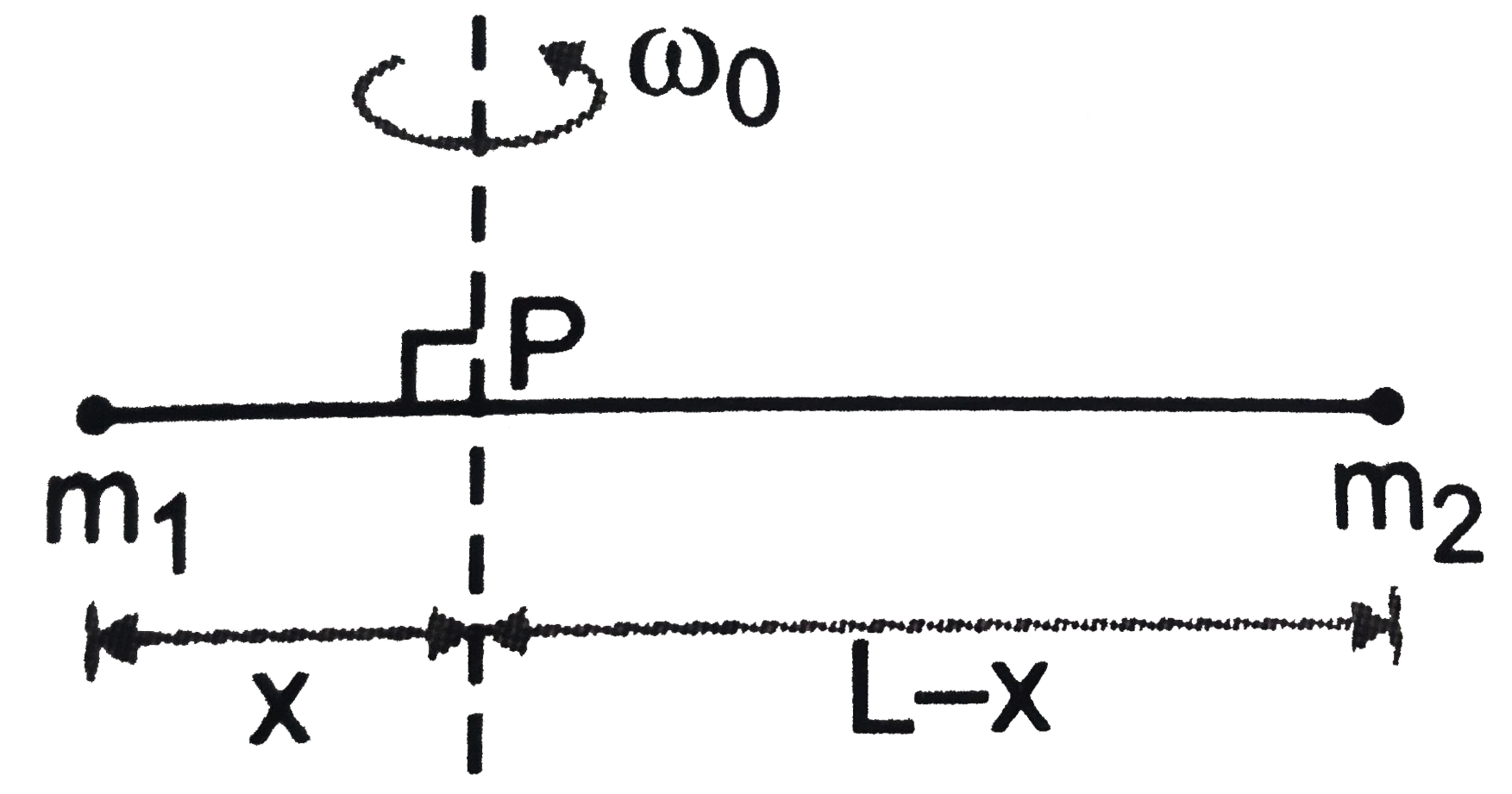 Ax=m2Lm1+m2Bx=m1Lm1+m2Cx=m1m2LDx=m2m1L
Ax=m2Lm1+m2Bx=m1Lm1+m2Cx=m1m2LDx=m2m1LTwo small spheres of mass 5kg and 15kg are joined by a rod of length 0.5m and of negligible mass. The M.I. of the system about an axis passing through centre of rod and normal to it is
A10kgm2B1.25kgm2C20kgm2D8kgm2
The radius of gyration of a uniform rod of mass m and length l about an axis perpendicular to its length and at distance l4 from its one end will be
View SolutionTwo point size bodies of masses 2kg,3kg are fixed at two ends of a light rod of length 1m. The moment of inertia of two bodies about an axis perpendicular to the length of rod and passing through centre of mass of two bodies is
View SolutionThe radius of gyration of an uniform rod of length L about an axis passing through its centre of mass and perpendicular to its length is.
View SolutionThe radius of gyration of a uniform rod of length l about an axis passing through one of its ends and perpendicular to its length is
View SolutionTwo bodies of mass 1 kg and 2 kg are attached to the ends of a 2 metre long weight less rod . This system is rotating about an axis passing through middle point of rod . Calculate M. I of system .
View Solution
