Two points charges , each Q , are fixed at separation 2d. A charged particle having charge q and mass m is placed between them.
(a) Now this charged particle is slightly displaced along the line joining the charges , slow that it will execute simple harmonic motion and find the time period of oscillation.
(b) If charge q is negative and it is displaced slightly perpendicular to the line joining the charges , repeat the part (a).
(a) Let the charged particle be displaced slightly towards right by distance x(x<<d).
(QatA,q):F1=14π∈0Qq(d−x)2 , towards left
(QatB,q):F2=14π∈0Qq(d+x)2 , towards right
F1>F2,Fnet=F1−F2 , will bring it towards O.
Restoring force F=−(F1−F2)
[negative sign shows that net force is towards origin]
=−14π∈0[1(d−x)2−1(d+x)2]
=−Qq4π∈0[4xd(d2−x2)2]
Since x<<d,x2 is negligible
=−Qqxπ∈0d3
Acceleration of charged particle is given as
a=Fm=−Qqπ∈0md3x ....(i)
aα−x
Acceleration α - (displacement) (Case of S.H.M.)
a=−ω2x .....(ii)
Comparing (i) and (ii) , we get
ω=√Qqπ∈0md3
Time period T=2πω=2π√π∈0md3Qq
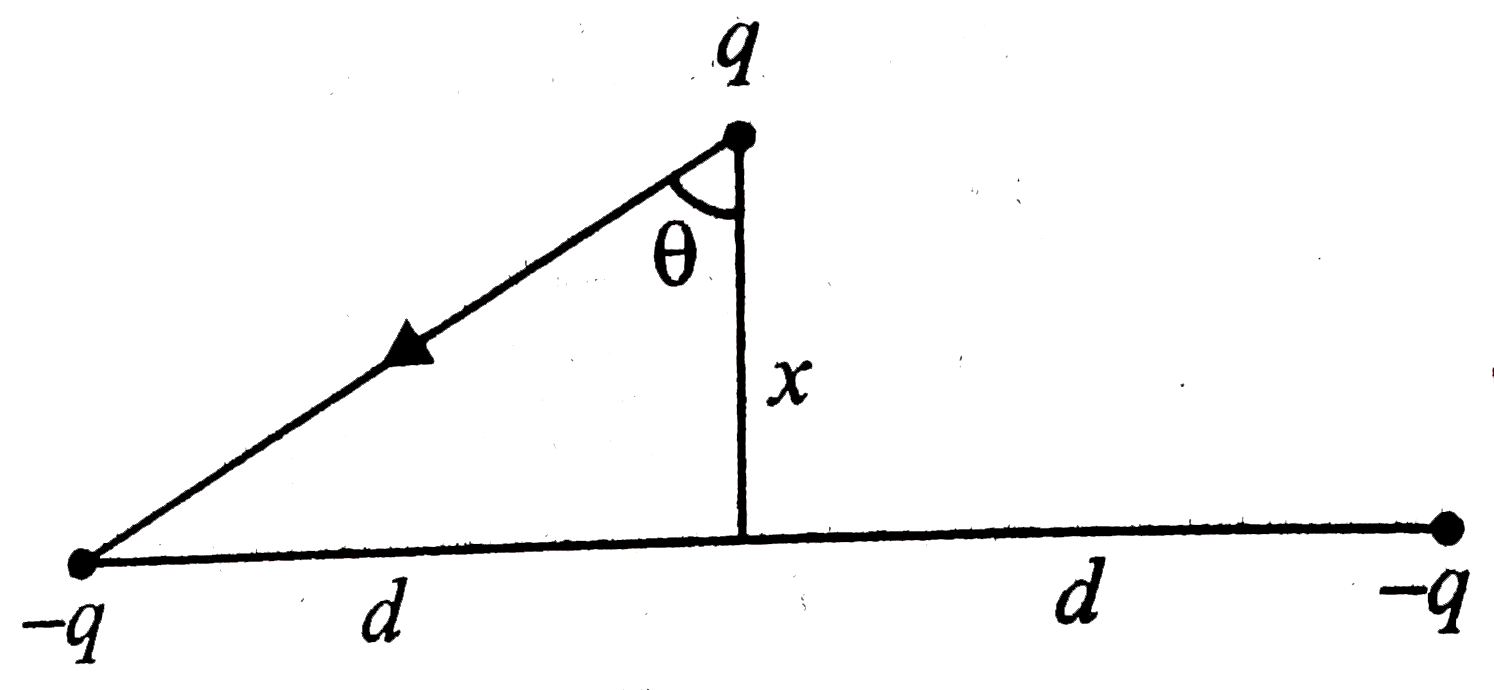
(b) Force on −q, by each QisF0, as shown
Restoring force is given as
F=−2F0cosθ
=−214π∈0.Qq(d2+x2).x(d2+x2)1/2
=−Qq2π∈0x(d2+x2)3/2
As x<<d,x2 is negligible
=−Qq2π∈0d3x
a=Fm=−Qq2π∈0md3x
aα−x (Case of S.H.M)
T=2π√2π∈0md3Qq
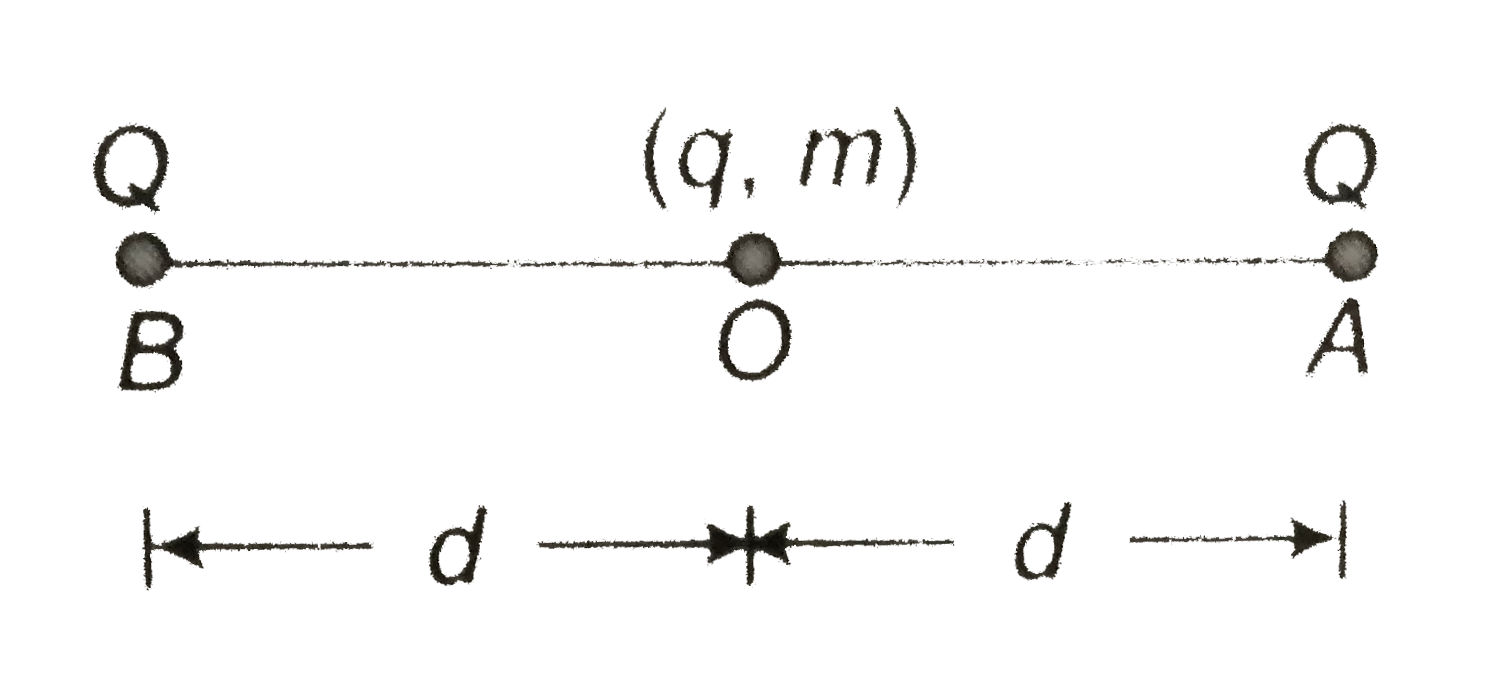
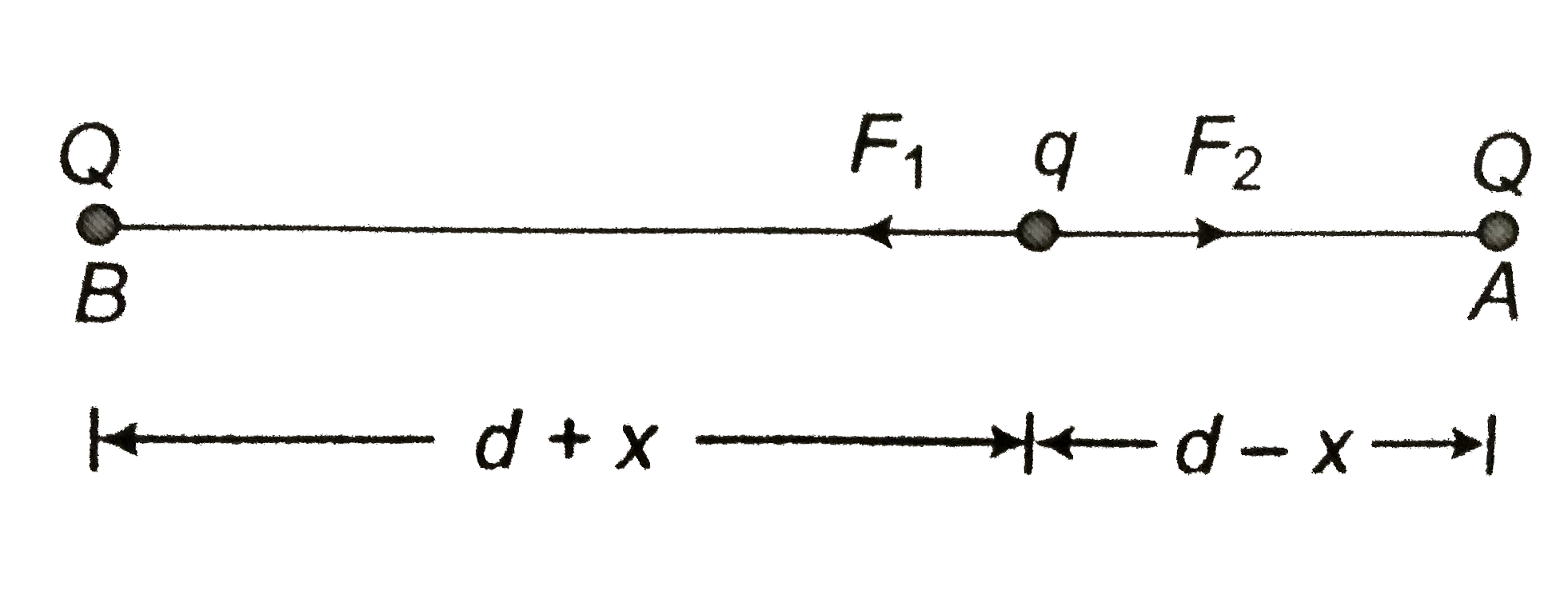
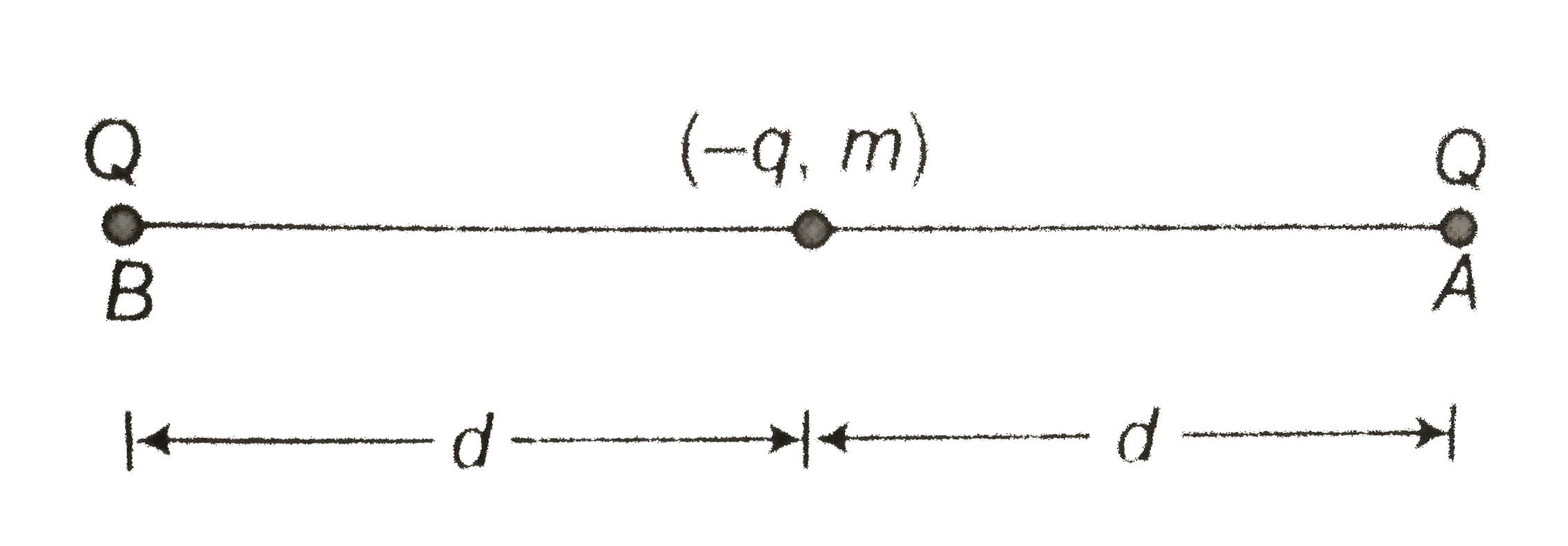
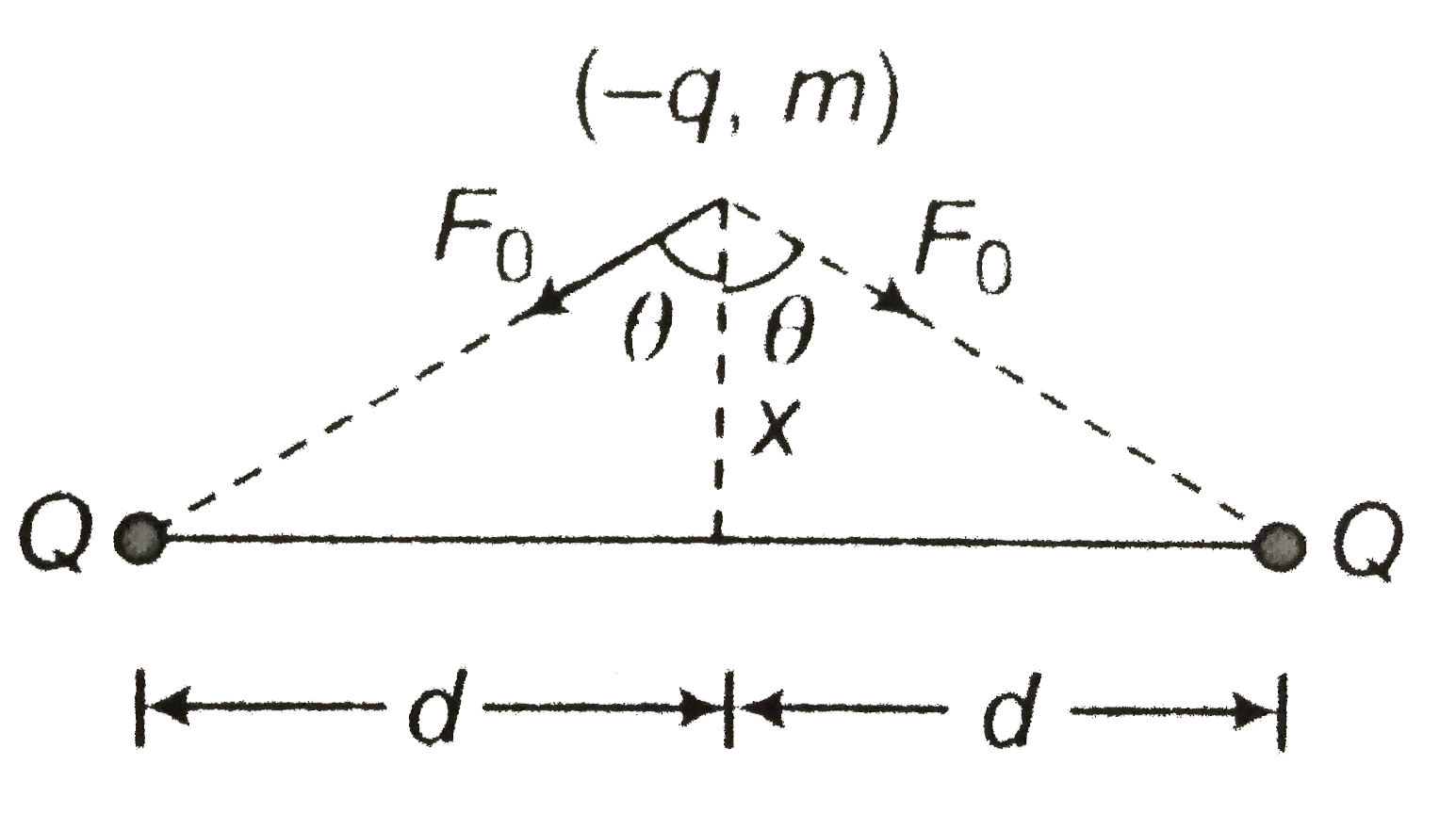
Topper's Solved these Questions
Similar Questions
A charged particle of mass m having charge q remains in equilibrium at height d above a fixed charge Q. Now the charged particle is slightly displaced along the line joining the charges, show that it will executes S.H.M. and find the time period of oscillation.
View SolutionTwo positive point charges , each Q , are fixed at separation d. A third charge q is placed in the middle. Describe the equilibrium of the third charge.
View Solution
Knowledge Check
Two identical charges +Q are kept fixed some distance apart.A small particles P with charge q is placed midway between them . If P is given a small displacement Δ ,it will undergo simple harmonic motion if
(i) q is positive and Δ is along the line joining the charges
(ii) q is positive and Δ is perpendicular to the line joining the charges
(iii) q is negative and Δ is perpendicular to the line joining the charges
(iv) q is positive and Δ is along the line joining the chargesA(i),(ii)B(i),(iii)C(ii),(iii)D(i),(iv)Two electrons each are fixed at a distance '2d'. A third charge proton placed at the midpoint is displaced slightly by a distance x(x<<d) perpendicular to the line joining the two fixed charges. Proton will execute simple harmonic motion having angular frequency : (m = mass of charged particle)
A(2q2πε0md3)12B(πε0md32q2)12C(q22πε0md3)12D(2πε0md3q2)12A negatively charged particle is situated on a striaght line joining two other charge particle stationary of motion of the negatively charged particle will depend on
Athe magnitude of chargeBthe position at which it is situatedCboth the magnitude of charge and its positionDthe magnitude of +q
Two indentical point charges having magnitude q each are placed as shown if fig. If we place a negative cahrge (of magnitude -q and mass m)at the midpoint of charges and displaced along the x-axis, examine whether it will perform simpe harmonic motion. If yes then find the time period of oscillation of the particle.

View SolutionTwo equal positive charges , Q , are fixed at points (0,d) and (0,−d) on the y-axis. A charged particle having charge −q and mass m is released from rest at point (d,0) on the x-axis . Discuss the motion of charged particle.
View SolutionTwo point charges+ q and-q are placed at distanced apart. What are the points at which the resultant field is parallel to the line joining the two charges ?
View SolutionA particle of mass m and charge q is located midway between two fixed charged particles each having a charge q and a distance 2l apart. Prove that the motion of the particle will be SHM if it is displaced slightly along the line connecting them and released. Also find its time period.
View SolutionTwo charges −q each are fixed separated by distance 2d. A third charge q of mass m placed at the mid-point is displaced at the mid-point is placed slightly by x(x<<d) perpendicular to the line joining the two fixed charges as shown in Fig. Show that q will perform simple harmonic oscillarion of time period.
T=[8π3∈0md3q2]1/2
View Solution
